
Question and Answers Forum
Question Number 158598 by HongKing last updated on 06/Nov/21
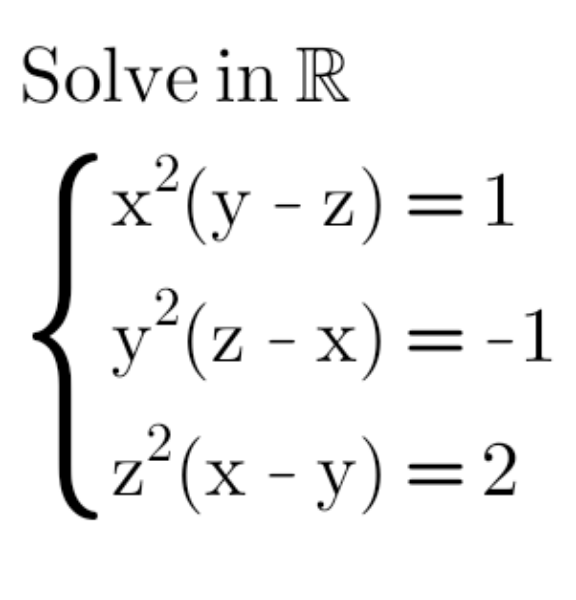
Commented by MJS_new last updated on 06/Nov/21
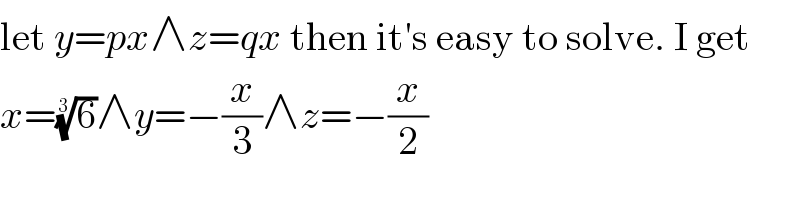
Commented by HongKing last updated on 06/Nov/21

Answered by Rasheed.Sindhi last updated on 06/Nov/21

Commented by HongKing last updated on 07/Nov/21

Commented by mr W last updated on 07/Nov/21
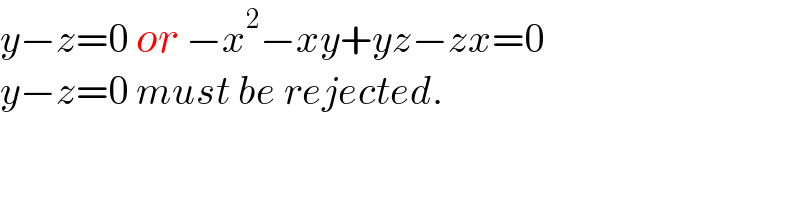
Commented by Rasheed.Sindhi last updated on 07/Nov/21
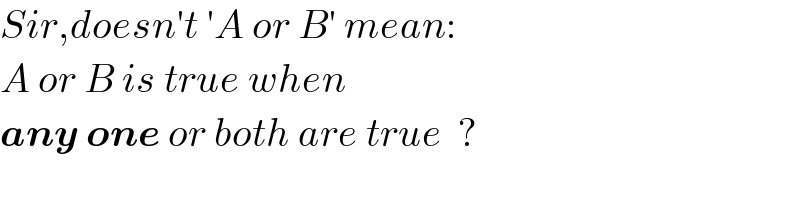
Commented by mr W last updated on 07/Nov/21
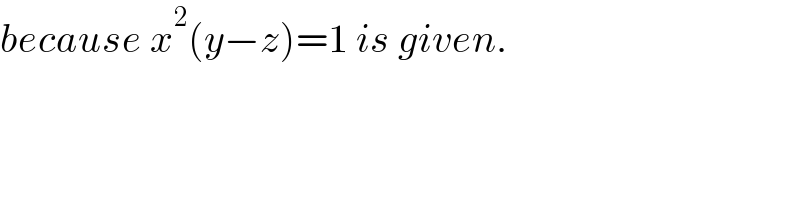
Commented by Rasheed.Sindhi last updated on 07/Nov/21

Commented by mr W last updated on 07/Nov/21
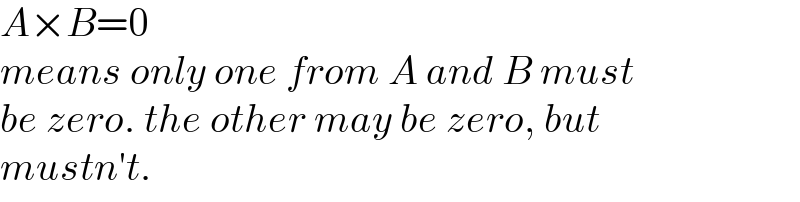
Commented by Rasheed.Sindhi last updated on 07/Nov/21
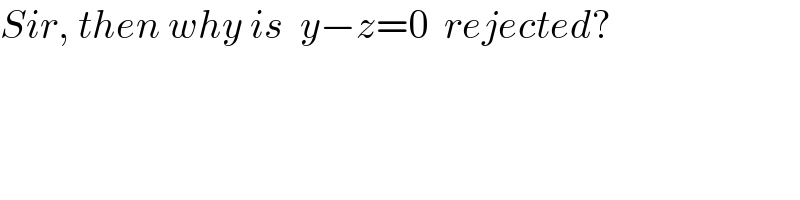
Answered by mr W last updated on 06/Nov/21
![((y^2 (z−x))/(x^2 (y−z)))=−1 ((y/x))^2 (((z/x)−1)/((y/x)−(z/x)))=−1 let p=(y/x), q=(z/x) p^2 (q−1)=−(p−q) (p−1)[(p+1)q−p]=0 ...(i) ((z^2 (x−y))/(x^2 (y−z)))=2 ((z/x))^2 ((1−(y/x))/((y/x)−(z/x)))=2 q^2 (1−p)=2(p−q) q(q+2)=(2+q^2 )p p=((q(q+2))/(2+q^2 )) ...(ii) case 1: from (i): p=1 from (ii): q=1 ⇒no solution case 2: from (i): (p+1)q−p=0 ⇒p=(q/(1−q)) ((q(q+2))/(2+q^2 ))=(q/(1−q)) q≠0 ((q+2)/(2+q^2 ))=(1/(1−q)) 2q^2 +q=0 2q+1=0 ⇒q=−(1/2) ⇒p=((−(1/2))/(1+(1/2)))=−(1/3) x^2 (−(x/3)+(x/2))=1 (x^3 /6)=1 ⇒x=(6)^(1/3) ⇒y=−((6)^(1/3) /3) ⇒z=−((6)^(1/3) /2)](Q158612.png)
Commented by HongKing last updated on 07/Nov/21
Commented by Tawa11 last updated on 07/Nov/21

