Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 15869 by prakash jain last updated on 14/Jun/17

If ax^2 +(b/x)≥c for all x,a,b>0 then prove minimum value of 27ab^2 is 4c^2 .

$$\mathrm{If}\:{ax}^{\mathrm{2}} +\frac{{b}}{{x}}\geqslant{c}\:\mathrm{for}\:\mathrm{all}\:{x},{a},{b}>\mathrm{0}\:\mathrm{then} \\ $$ $$\mathrm{prove}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of} \\ $$ $$\mathrm{27}{ab}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{4}{c}^{\mathrm{2}} . \\ $$

Commented byprakash jain last updated on 14/Jun/17

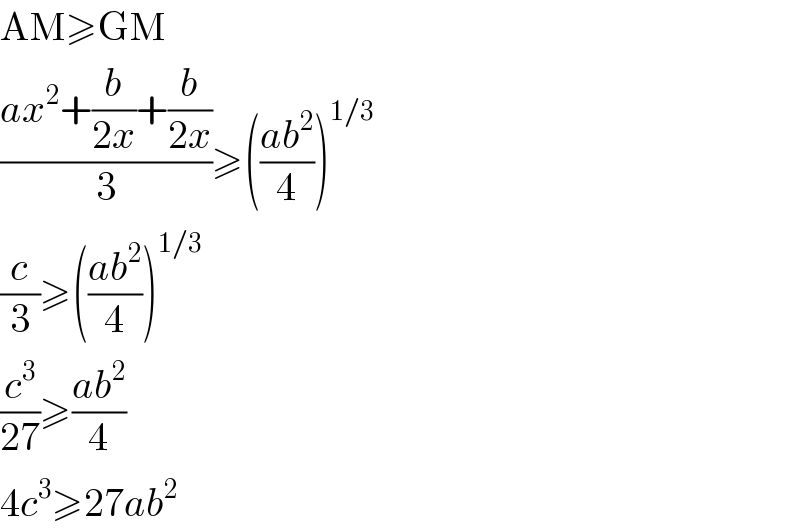
AM≥GM ((ax^2 +(b/(2x))+(b/(2x)))/3)≥(((ab^2 )/4))^(1/3) (c/3)≥(((ab^2 )/4))^(1/3) (c^3 /(27))≥((ab^2 )/4) 4c^3 ≥27ab^2

$$\mathrm{AM}\geqslant\mathrm{GM} \\ $$ $$\frac{{ax}^{\mathrm{2}} +\frac{{b}}{\mathrm{2}{x}}+\frac{{b}}{\mathrm{2}{x}}}{\mathrm{3}}\geqslant\left(\frac{{ab}^{\mathrm{2}} }{\mathrm{4}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$ $$\frac{{c}}{\mathrm{3}}\geqslant\left(\frac{{ab}^{\mathrm{2}} }{\mathrm{4}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$ $$\frac{{c}^{\mathrm{3}} }{\mathrm{27}}\geqslant\frac{{ab}^{\mathrm{2}} }{\mathrm{4}} \\ $$ $$\mathrm{4}{c}^{\mathrm{3}} \geqslant\mathrm{27}{ab}^{\mathrm{2}} \\ $$

Answered by ajfour last updated on 15/Jun/17

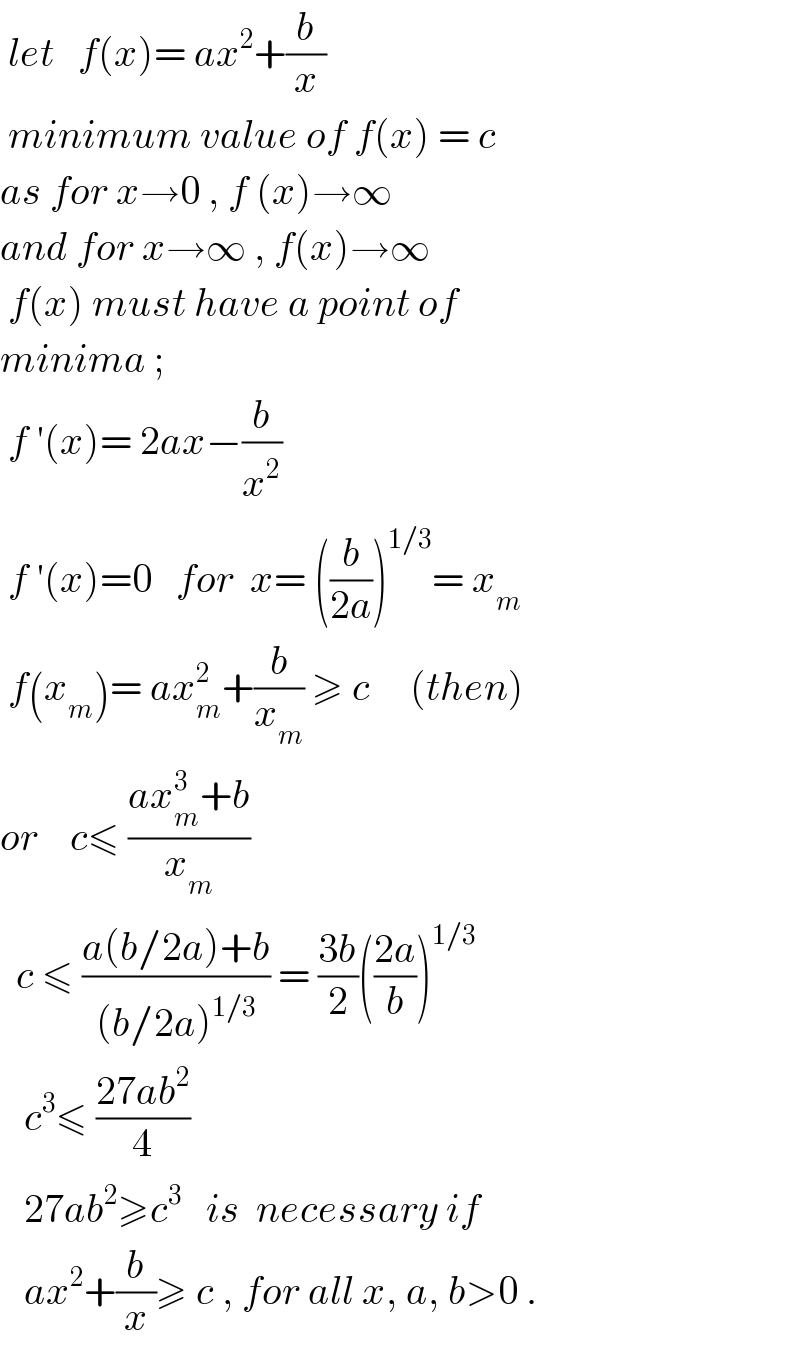
let f(x)= ax^2 +(b/x) minimum value of f(x) = c as for x→0 , f (x)→∞ and for x→∞ , f(x)→∞ f(x) must have a point of minima ; f ′(x)= 2ax−(b/x^2 ) f ′(x)=0 for x= ((b/(2a)))^(1/3) = x_m f(x_m )= ax_m ^2 +(b/x_m ) ≥ c (then) or c≤ ((ax_m ^3 +b)/x_m ) c ≤ ((a(b/2a)+b)/((b/2a)^(1/3) )) = ((3b)/2)(((2a)/b))^(1/3) c^3 ≤ ((27ab^2 )/4) 27ab^2 ≥c^3 is necessary if ax^2 +(b/x)≥ c , for all x, a, b>0 .

$$\:{let}\:\:\:{f}\left({x}\right)=\:{ax}^{\mathrm{2}} +\frac{{b}}{{x}} \\ $$ $$\:{minimum}\:{value}\:{of}\:{f}\left({x}\right)\:=\:{c} \\ $$ $${as}\:{for}\:{x}\rightarrow\mathrm{0}\:,\:{f}\:\left({x}\right)\rightarrow\infty \\ $$ $${and}\:{for}\:{x}\rightarrow\infty\:,\:{f}\left({x}\right)\rightarrow\infty \\ $$ $$\:{f}\left({x}\right)\:{must}\:{have}\:{a}\:{point}\:{of}\: \\ $$ $${minima}\:; \\ $$ $$\:{f}\:'\left({x}\right)=\:\mathrm{2}{ax}−\frac{{b}}{{x}^{\mathrm{2}} } \\ $$ $$\:{f}\:'\left({x}\right)=\mathrm{0}\:\:\:{for}\:\:{x}=\:\left(\frac{{b}}{\mathrm{2}{a}}\right)^{\mathrm{1}/\mathrm{3}} =\:{x}_{{m}} \\ $$ $$\:{f}\left({x}_{{m}} \right)=\:{ax}_{{m}} ^{\mathrm{2}} +\frac{{b}}{{x}_{{m}} }\:\geqslant\:{c}\:\:\:\:\:\left({then}\right) \\ $$ $${or}\:\:\:\:{c}\leqslant\:\frac{{ax}_{{m}} ^{\mathrm{3}} +{b}}{{x}_{{m}} } \\ $$ $$\:\:{c}\:\leqslant\:\frac{{a}\left({b}/\mathrm{2}{a}\right)+{b}}{\left({b}/\mathrm{2}{a}\right)^{\mathrm{1}/\mathrm{3}} }\:=\:\frac{\mathrm{3}{b}}{\mathrm{2}}\left(\frac{\mathrm{2}{a}}{{b}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$ $$\:\:\:{c}^{\mathrm{3}} \leqslant\:\frac{\mathrm{27}{ab}^{\mathrm{2}} }{\mathrm{4}}\: \\ $$ $$\:\:\:\mathrm{27}{ab}^{\mathrm{2}} \geqslant{c}^{\mathrm{3}} \:\:\:{is}\:\:{necessary}\:{if} \\ $$ $$\:\:\:{ax}^{\mathrm{2}} +\frac{{b}}{{x}}\geqslant\:{c}\:,\:{for}\:{all}\:{x},\:{a},\:{b}>\mathrm{0}\:. \\ $$

Commented byprakash jain last updated on 15/Jun/17

Thanks.

$$\mathrm{Thanks}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com