Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 158781 by HongKing last updated on 08/Nov/21

Answered by MJS_new last updated on 09/Nov/21

∫_0 ^π (((1+sin^2 2x)cos 4x)/(1+asin^2 x))dx=2∫_0 ^(π/2) (((1+sin^2 2x)cos 4x)/(1+asin^2 x)) [t=tan x → dx=(dt/(t^2 +1))] =2∫_0 ^∞ ((t^8 −34t^4 +1)/((t^2 +1)^4 ((a+1)t^2 +1)))dx= [Ostrogradski′s Method] =−[((8t(3(a+1)(a−4)t^4 +(7a^2 −24a−24)t^2 −3(5a+4)))/(3a^3 (t^2 +1)^3 ))]_0 ^∞ + −((8(a+2)(a^2 −4a−4))/a^4 )∫_0 ^∞ (dt/(t^2 +1))+ +((2(a^2 −4a−4)(a^2 +8a+8))/a^4 )∫_0 ^∞ (dt/((a+1)t^2 +1))= =−[((8t(3(a+1)(a−4)t^4 +(7a^2 −24a−24)t^2 −3(5a+4)))/(3a^3 (t^2 +1)^3 ))]_0 ^∞ − −[((8(a+2)(a^2 −4a−4))/a^4 )arctan t]_0 ^∞ + +[((2(a^2 −4a−4)(a^2 +8a+8))/(a^4 (√(a+1))))arctan ((√(a+1))t)]_0 ^∞ = =(((a^2 −4a−4)(a^2 +8a+8−4(a+2)(√(a+1))))/(a^4 (√(a+1))))π (π/a)+(((a^2 −4a−4)(a^2 +8a+8−4(a+2)(√(a+1))))/(a^4 (√(a+1))))π=0 ⇒ (3a^3 −8a^2 −48a−32)(√(a+1))=(a^2 −4a−4)(a^2 +8a+8) squaring & transforming a^3 (a^5 −a^4 −a^3 −80a^2 −144a−64)=0 a≠0 ⇒ answer is 2 but still the only solution for a is <0 a≈−.938890161126

$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}\right)\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{1}+{a}\mathrm{sin}^{\mathrm{2}} \:{x}}{dx}=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}\right)\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{1}+{a}\mathrm{sin}^{\mathrm{2}} \:{x}} \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{t}^{\mathrm{8}} −\mathrm{34}{t}^{\mathrm{4}} +\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} \left(\left({a}+\mathrm{1}\right){t}^{\mathrm{2}} +\mathrm{1}\right)}{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=−\left[\frac{\mathrm{8}{t}\left(\mathrm{3}\left({a}+\mathrm{1}\right)\left({a}−\mathrm{4}\right){t}^{\mathrm{4}} +\left(\mathrm{7}{a}^{\mathrm{2}} −\mathrm{24}{a}−\mathrm{24}\right){t}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{5}{a}+\mathrm{4}\right)\right)}{\mathrm{3}{a}^{\mathrm{3}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\right]_{\mathrm{0}} ^{\infty} + \\ $$$$−\frac{\mathrm{8}\left({a}+\mathrm{2}\right)\left({a}^{\mathrm{2}} −\mathrm{4}{a}−\mathrm{4}\right)}{{a}^{\mathrm{4}} }\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}+ \\ $$$$+\frac{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{4}{a}−\mathrm{4}\right)\left({a}^{\mathrm{2}} +\mathrm{8}{a}+\mathrm{8}\right)}{{a}^{\mathrm{4}} }\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{\left({a}+\mathrm{1}\right){t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=−\left[\frac{\mathrm{8}{t}\left(\mathrm{3}\left({a}+\mathrm{1}\right)\left({a}−\mathrm{4}\right){t}^{\mathrm{4}} +\left(\mathrm{7}{a}^{\mathrm{2}} −\mathrm{24}{a}−\mathrm{24}\right){t}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{5}{a}+\mathrm{4}\right)\right)}{\mathrm{3}{a}^{\mathrm{3}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\right]_{\mathrm{0}} ^{\infty} − \\ $$$$−\left[\frac{\mathrm{8}\left({a}+\mathrm{2}\right)\left({a}^{\mathrm{2}} −\mathrm{4}{a}−\mathrm{4}\right)}{{a}^{\mathrm{4}} }\mathrm{arctan}\:{t}\right]_{\mathrm{0}} ^{\infty} + \\ $$$$+\left[\frac{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{4}{a}−\mathrm{4}\right)\left({a}^{\mathrm{2}} +\mathrm{8}{a}+\mathrm{8}\right)}{{a}^{\mathrm{4}} \sqrt{{a}+\mathrm{1}}}\mathrm{arctan}\:\left(\sqrt{{a}+\mathrm{1}}{t}\right)\right]_{\mathrm{0}} ^{\infty} = \\ $$$$=\frac{\left({a}^{\mathrm{2}} −\mathrm{4}{a}−\mathrm{4}\right)\left({a}^{\mathrm{2}} +\mathrm{8}{a}+\mathrm{8}−\mathrm{4}\left({a}+\mathrm{2}\right)\sqrt{{a}+\mathrm{1}}\right)}{{a}^{\mathrm{4}} \sqrt{{a}+\mathrm{1}}}\pi \\ $$$$ \\ $$$$\frac{\pi}{{a}}+\frac{\left({a}^{\mathrm{2}} −\mathrm{4}{a}−\mathrm{4}\right)\left({a}^{\mathrm{2}} +\mathrm{8}{a}+\mathrm{8}−\mathrm{4}\left({a}+\mathrm{2}\right)\sqrt{{a}+\mathrm{1}}\right)}{{a}^{\mathrm{4}} \sqrt{{a}+\mathrm{1}}}\pi=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{3}{a}^{\mathrm{3}} −\mathrm{8}{a}^{\mathrm{2}} −\mathrm{48}{a}−\mathrm{32}\right)\sqrt{{a}+\mathrm{1}}=\left({a}^{\mathrm{2}} −\mathrm{4}{a}−\mathrm{4}\right)\left({a}^{\mathrm{2}} +\mathrm{8}{a}+\mathrm{8}\right) \\ $$$$\mathrm{squaring}\:\&\:\mathrm{transforming} \\ $$$${a}^{\mathrm{3}} \left({a}^{\mathrm{5}} −{a}^{\mathrm{4}} −{a}^{\mathrm{3}} −\mathrm{80}{a}^{\mathrm{2}} −\mathrm{144}{a}−\mathrm{64}\right)=\mathrm{0} \\ $$$${a}\neq\mathrm{0}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{2} \\ $$$$\mathrm{but}\:\mathrm{still}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:\mathrm{for}\:{a}\:\mathrm{is}\:<\mathrm{0} \\ $$$${a}\approx−.\mathrm{938890161126} \\ $$

Commented by HongKing last updated on 09/Nov/21

thank you so much my dear Ser, but its not correct, check from the 6th line..

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er}, \\ $$$$\mathrm{but}\:\mathrm{its}\:\mathrm{not}\:\mathrm{correct},\:\mathrm{check}\:\mathrm{from}\:\mathrm{the} \\ $$$$\mathrm{6th}\:\mathrm{line}.. \\ $$

Commented by HongKing last updated on 09/Nov/21

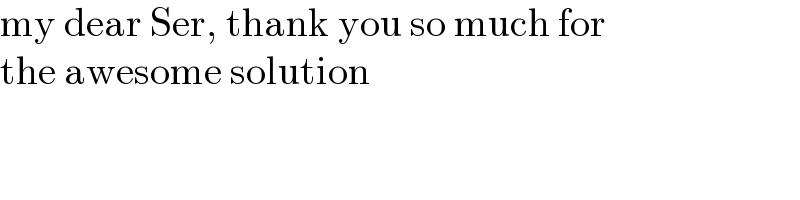
my dear Ser, thank you so much for the awesome solution

$$\mathrm{my}\:\mathrm{dear}\:\mathrm{Ser},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{for} \\ $$$$\mathrm{the}\:\mathrm{awesome}\:\mathrm{solution} \\ $$

Commented by MJS_new last updated on 09/Nov/21

corrected it

$$\mathrm{corrected}\:\mathrm{it} \\ $$

Answered by ajfour last updated on 09/Nov/21

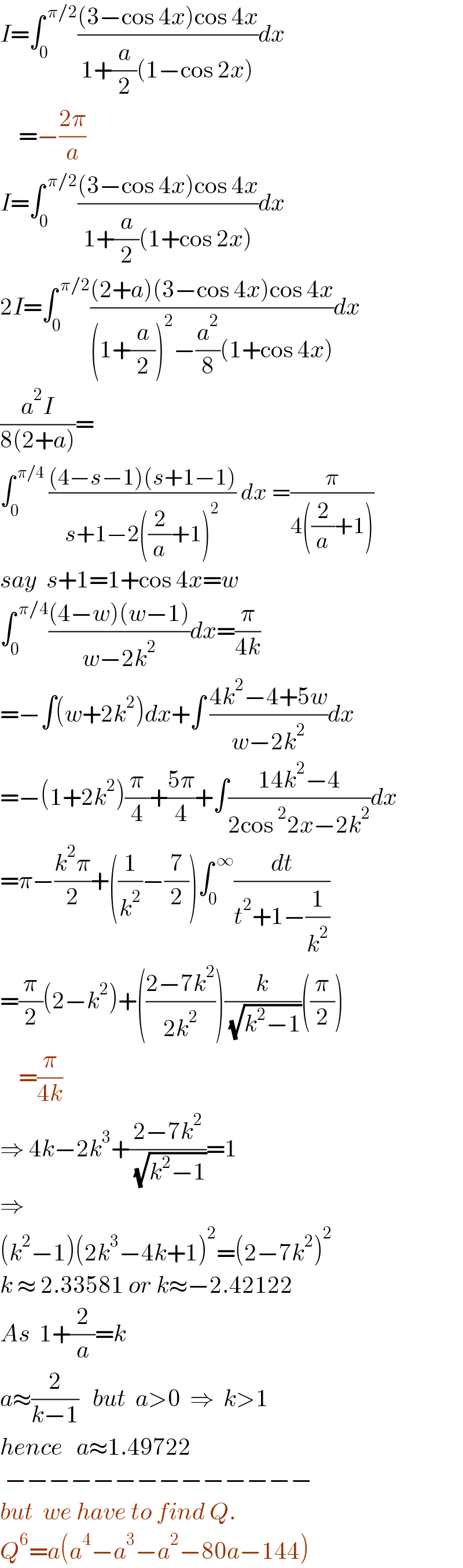
I=∫_0 ^( π/2) (((3−cos 4x)cos 4x)/(1+(a/2)(1−cos 2x)))dx =−((2π)/a) I=∫_0 ^( π/2) (((3−cos 4x)cos 4x)/(1+(a/2)(1+cos 2x)))dx 2I=∫_0 ^( π/2) (((2+a)(3−cos 4x)cos 4x)/((1+(a/2))^2 −(a^2 /8)(1+cos 4x)))dx ((a^2 I)/(8(2+a)))= ∫_0 ^( π/4) (((4−s−1)(s+1−1))/(s+1−2((2/a)+1)^2 )) dx =(π/(4((2/a)+1))) say s+1=1+cos 4x=w ∫_0 ^( π/4) (((4−w)(w−1))/(w−2k^2 ))dx=(π/(4k)) =−∫(w+2k^2 )dx+∫ ((4k^2 −4+5w)/(w−2k^2 ))dx =−(1+2k^2 )(π/4)+((5π)/4)+∫((14k^2 −4)/(2cos^2 2x−2k^2 ))dx =π−((k^2 π)/2)+((1/k^2 )−(7/2))∫_0 ^( ∞) (dt/(t^2 +1−(1/k^2 ))) =(π/2)(2−k^2 )+(((2−7k^2 )/(2k^2 )))(k/( (√(k^2 −1))))((π/2)) =(π/(4k)) ⇒ 4k−2k^3 +((2−7k^2 )/( (√(k^2 −1))))=1 ⇒ (k^2 −1)(2k^3 −4k+1)^2 =(2−7k^2 )^2 k ≈ 2.33581 or k≈−2.42122 As 1+(2/a)=k a≈(2/(k−1)) but a>0 ⇒ k>1 hence a≈1.49722 −−−−−−−−−−−−−− but we have to find Q. Q^6 =a(a^4 −a^3 −a^2 −80a−144)

$${I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\left(\mathrm{3}−\mathrm{cos}\:\mathrm{4}{x}\right)\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{1}+\frac{{a}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)}{dx} \\ $$$$\:\:\:\:=−\frac{\mathrm{2}\pi}{{a}} \\ $$$${I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\left(\mathrm{3}−\mathrm{cos}\:\mathrm{4}{x}\right)\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{1}+\frac{{a}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}\right)}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\left(\mathrm{2}+{a}\right)\left(\mathrm{3}−\mathrm{cos}\:\mathrm{4}{x}\right)\mathrm{cos}\:\mathrm{4}{x}}{\left(\mathrm{1}+\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{4}{x}\right)}{dx} \\ $$$$\frac{{a}^{\mathrm{2}} {I}}{\mathrm{8}\left(\mathrm{2}+{a}\right)}= \\ $$$$\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \:\frac{\left(\mathrm{4}−{s}−\mathrm{1}\right)\left({s}+\mathrm{1}−\mathrm{1}\right)}{{s}+\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{2}}{{a}}+\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\:=\frac{\pi}{\mathrm{4}\left(\frac{\mathrm{2}}{{a}}+\mathrm{1}\right)} \\ $$$${say}\:\:{s}+\mathrm{1}=\mathrm{1}+\mathrm{cos}\:\mathrm{4}{x}={w} \\ $$$$\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \frac{\left(\mathrm{4}−{w}\right)\left({w}−\mathrm{1}\right)}{{w}−\mathrm{2}{k}^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{4}{k}} \\ $$$$=−\int\left({w}+\mathrm{2}{k}^{\mathrm{2}} \right){dx}+\int\:\frac{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{4}+\mathrm{5}{w}}{{w}−\mathrm{2}{k}^{\mathrm{2}} }{dx} \\ $$$$=−\left(\mathrm{1}+\mathrm{2}{k}^{\mathrm{2}} \right)\frac{\pi}{\mathrm{4}}+\frac{\mathrm{5}\pi}{\mathrm{4}}+\int\frac{\mathrm{14}{k}^{\mathrm{2}} −\mathrm{4}}{\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2}{x}−\mathrm{2}{k}^{\mathrm{2}} }{dx} \\ $$$$=\pi−\frac{{k}^{\mathrm{2}} \pi}{\mathrm{2}}+\left(\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\frac{\mathrm{7}}{\mathrm{2}}\right)\int_{\mathrm{0}} ^{\:\infty} \frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}−\frac{\mathrm{1}}{{k}^{\mathrm{2}} }} \\ $$$$=\frac{\pi}{\mathrm{2}}\left(\mathrm{2}−{k}^{\mathrm{2}} \right)+\left(\frac{\mathrm{2}−\mathrm{7}{k}^{\mathrm{2}} }{\mathrm{2}{k}^{\mathrm{2}} }\right)\frac{{k}}{\:\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{4}{k}} \\ $$$$\Rightarrow\:\mathrm{4}{k}−\mathrm{2}{k}^{\mathrm{3}} +\frac{\mathrm{2}−\mathrm{7}{k}^{\mathrm{2}} }{\:\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}}=\mathrm{1} \\ $$$$\Rightarrow\: \\ $$$$\left({k}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2}{k}^{\mathrm{3}} −\mathrm{4}{k}+\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{2}−\mathrm{7}{k}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${k}\:\approx\:\mathrm{2}.\mathrm{33581}\:{or}\:{k}\approx−\mathrm{2}.\mathrm{42122} \\ $$$${As}\:\:\mathrm{1}+\frac{\mathrm{2}}{{a}}={k} \\ $$$${a}\approx\frac{\mathrm{2}}{{k}−\mathrm{1}}\:\:\:{but}\:\:{a}>\mathrm{0}\:\:\Rightarrow\:\:{k}>\mathrm{1} \\ $$$${hence}\:\:\:{a}\approx\mathrm{1}.\mathrm{49722} \\ $$$$\:−−−−−−−−−−−−−− \\ $$$${but}\:\:{we}\:{have}\:{to}\:{find}\:{Q}. \\ $$$${Q}^{\mathrm{6}} ={a}\left({a}^{\mathrm{4}} −{a}^{\mathrm{3}} −{a}^{\mathrm{2}} −\mathrm{80}{a}−\mathrm{144}\right) \\ $$

Commented by HongKing last updated on 10/Nov/21

thank you so much my dear Ser

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Ser} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com