Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 158794 by SANOGO last updated on 08/Nov/21

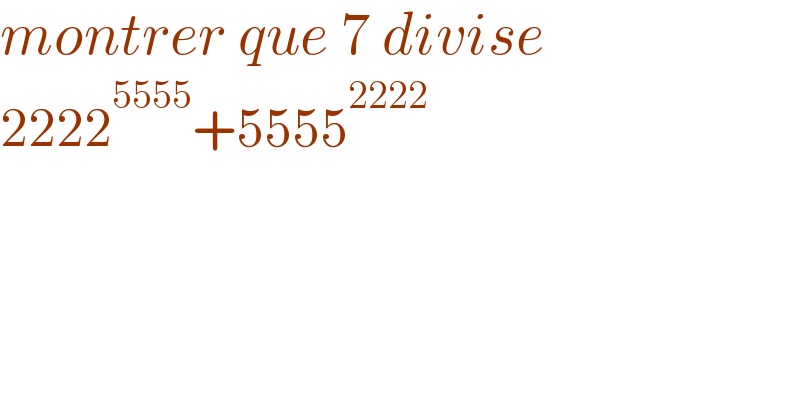
montrer que 7 divise 2222^(5555) +5555^(2222)

$${montrer}\:{que}\:\mathrm{7}\:{divise} \\ $$$$\mathrm{2222}^{\mathrm{5555}} +\mathrm{5555}^{\mathrm{2222}} \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 09/Nov/21

We′ll determine remainders of 2222^(5555) & 5555^(2222) separately and then add them: ▶2222^(5555) ≡x(mod 7) 2222≡3(mod 7) 2222^5 ≡3^5 ≡5(mod 7)..........(i) ∵gcd(2222,7)=1 & φ(7)=6 ∴2222^6 ≡1(mod 7) (2222^6 )^(925) ≡(1)^(925) (mod 7) 2222^(5550) ≡1(mod 7)............(ii) (i)×(ii): 2222^5 .2222^(5550) ≡5.1(mod 7) 2222^(5555) ≡5(mod 7).............A ▶5555^(2222) ≡y(mod 7) gcd(5555,7)=1 & φ(7)=6 5555^6 ≡1(mod 7) (5555^6 )^(370) ≡(1)^(370) (mod 7) 5555^(2220) ≡1(mod 7)........(iii) 5555≡4(mod 7) 5555^2 ≡4^2 ≡2(mod 7)........(iv) (iii)×(iv): 5555^(2222) ≡2(mod 7).................B A+B: 2222^(5555) +5555^(2222) ≡5+2≡0(mod 7) Hence 7 divides given expression. determinant (((a^(φ(m)) ≡1(mod m)_(provided that gcd(a,m)=1) )))^ ^(≼FORMULA USED≽_( ) ^( ) )

$${We}'{ll}\:\:{determine}\:{remainders} \\ $$$${of}\:\mathrm{2222}^{\mathrm{5555}} \:\&\:\mathrm{5555}^{\mathrm{2222}} \:{separately} \\ $$$${and}\:{then}\:{add}\:{them}: \\ $$$$\blacktriangleright\mathrm{2222}^{\mathrm{5555}} \equiv{x}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\:\mathrm{2222}\equiv\mathrm{3}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\:\mathrm{2222}^{\mathrm{5}} \equiv\mathrm{3}^{\mathrm{5}} \equiv\mathrm{5}\left({mod}\:\mathrm{7}\right)..........\left({i}\right) \\ $$$$\because\mathrm{gcd}\left(\mathrm{2222},\mathrm{7}\right)=\mathrm{1}\:\&\:\phi\left(\mathrm{7}\right)=\mathrm{6} \\ $$$$\therefore\mathrm{2222}^{\mathrm{6}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\left(\mathrm{2222}^{\mathrm{6}} \right)^{\mathrm{925}} \equiv\left(\mathrm{1}\right)^{\mathrm{925}} \left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\mathrm{2222}^{\mathrm{5550}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right)............\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right): \\ $$$$\:\:\:\:\mathrm{2222}^{\mathrm{5}} .\mathrm{2222}^{\mathrm{5550}} \equiv\mathrm{5}.\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\mathrm{2222}^{\mathrm{5555}} \equiv\mathrm{5}\left({mod}\:\mathrm{7}\right).............{A} \\ $$$$\blacktriangleright\mathrm{5555}^{\mathrm{2222}} \equiv{y}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\mathrm{gcd}\left(\mathrm{5555},\mathrm{7}\right)=\mathrm{1}\:\&\:\phi\left(\mathrm{7}\right)=\mathrm{6} \\ $$$$\:\:\:\:\mathrm{5555}^{\mathrm{6}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\left(\mathrm{5555}^{\mathrm{6}} \right)^{\mathrm{370}} \equiv\left(\mathrm{1}\right)^{\mathrm{370}} \left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\mathrm{5555}^{\mathrm{2220}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right)........\left({iii}\right) \\ $$$$\:\:\:\:\mathrm{5555}\equiv\mathrm{4}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\mathrm{5555}^{\mathrm{2}} \equiv\mathrm{4}^{\mathrm{2}} \equiv\mathrm{2}\left({mod}\:\mathrm{7}\right)........\left({iv}\right) \\ $$$$\left({iii}\right)×\left({iv}\right): \\ $$$$\:\:\:\:\mathrm{5555}^{\mathrm{2222}} \equiv\mathrm{2}\left({mod}\:\mathrm{7}\right).................{B} \\ $$$${A}+{B}: \\ $$$$\:\:\:\:\mathrm{2222}^{\mathrm{5555}} +\mathrm{5555}^{\mathrm{2222}} \equiv\mathrm{5}+\mathrm{2}\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\mathcal{H}{ence}\:\mathrm{7}\:{divides}\:{given}\:{expression}. \\ $$$$\:\:\overset{\preccurlyeq\underset{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} {\overset{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} {\mathrm{FORMULA}\:\mathrm{USED}\succcurlyeq}}} {\begin{array}{|c|}{\underset{{provided}\:{that}\:\mathrm{gcd}\left({a},{m}\right)=\mathrm{1}} {{a}^{\phi\left({m}\right)} \equiv\mathrm{1}\left({mod}\:{m}\right)}}\\\hline\end{array}^{} } \\ $$

Commented by SANOGO last updated on 09/Nov/21

merci bien

$${merci}\:{bien} \\ $$

Answered by Rasheed.Sindhi last updated on 09/Nov/21

MOD 7 2222^(5555) +5555^(2222) =2222^(6×925+5) +5555^(6×370+2) [∵φ(7)=6] =(2222^6 )^(925) .2222^5 +(5555^6 )^(370) .5555^2 =(1^(925) )(2222^5 +(1^(370) )(5555^2 ) [ ∵2222^6 ≡1 & 5555^6 ≡1(mod 7)] =2222^5 +5555^2 =3^5 +4^2 [∵2222≡3 & 5555≡4 (mod 7)] =5+2=7=0 Hence 7 ∣ (2222^(5555) +5555^(2222) )

$$\:\:\:\:\:\:\mathrm{MOD}\:\mathrm{7} \\ $$$$\mathrm{2222}^{\mathrm{5555}} +\mathrm{5555}^{\mathrm{2222}} \\ $$$$=\mathrm{2222}^{\mathrm{6}×\mathrm{925}+\mathrm{5}} +\mathrm{5555}^{\mathrm{6}×\mathrm{370}+\mathrm{2}} \left[\because\phi\left(\mathrm{7}\right)=\mathrm{6}\right] \\ $$$$=\left(\mathrm{2222}^{\mathrm{6}} \right)^{\mathrm{925}} .\mathrm{2222}^{\mathrm{5}} +\left(\mathrm{5555}^{\mathrm{6}} \right)^{\mathrm{370}} .\mathrm{5555}^{\mathrm{2}} \\ $$$$=\left(\mathrm{1}^{\mathrm{925}} \right)\left(\mathrm{2222}^{\mathrm{5}} +\left(\mathrm{1}^{\mathrm{370}} \right)\left(\mathrm{5555}^{\mathrm{2}} \right)\right. \\ $$$$\:\:\:\:\:\:\:\:\:\left[\:\because\mathrm{2222}^{\mathrm{6}} \equiv\mathrm{1}\:\&\:\mathrm{5555}^{\mathrm{6}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right)\right] \\ $$$$=\mathrm{2222}^{\mathrm{5}} +\mathrm{5555}^{\mathrm{2}} \\ $$$$=\mathrm{3}^{\mathrm{5}} +\mathrm{4}^{\mathrm{2}} \:\left[\because\mathrm{2222}\equiv\mathrm{3}\:\&\:\mathrm{5555}\equiv\mathrm{4}\:\left({mod}\:\mathrm{7}\right)\right] \\ $$$$=\mathrm{5}+\mathrm{2}=\mathrm{7}=\mathrm{0} \\ $$$${Hence}\: \\ $$$$\:\:\:\:\:\:\mathrm{7}\:\mid\:\left(\mathrm{2222}^{\mathrm{5555}} +\mathrm{5555}^{\mathrm{2222}} \right) \\ $$

Commented by SANOGO last updated on 10/Nov/21

merci bien

$${merci}\:{bien} \\ $$

Commented by SANOGO last updated on 10/Nov/21

merci bien

$${merci}\:{bien} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com