Question and Answers Forum
Question Number 158874 by ajfour last updated on 09/Nov/21
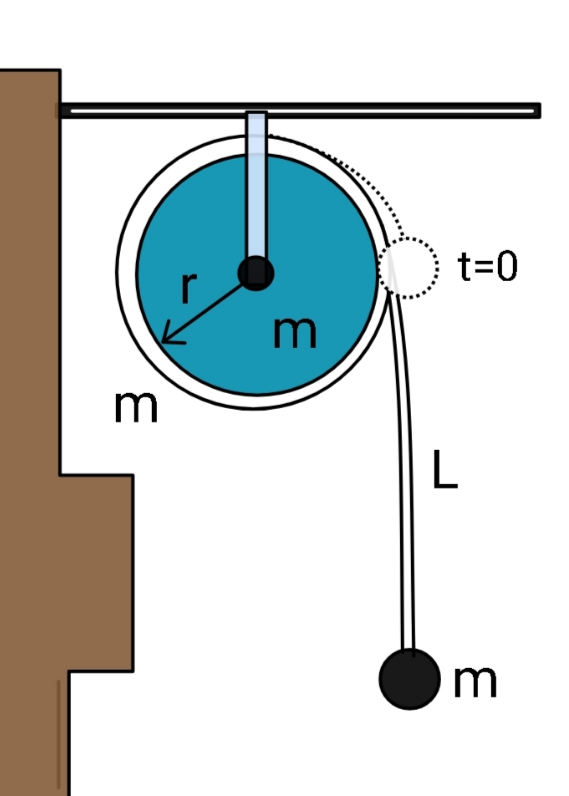
Commented by ajfour last updated on 09/Nov/21

Answered by mr W last updated on 10/Nov/21
![at time t: I=((mr^2 )/2)+(1−(x/L))mr^2 =((mr^2 )/2)(3−((2x)/L)) M=m+(x/L)m=(1+(x/L))m ω=(v/r) v=(dx/dt) T=tension in hanging rope at pulley ((d(Iω))/dt)=Tr ((mr)/2)(3−((2x)/L))(dv/dt)−((mr)/2)×(2/L)v^2 =Tr ((3/2)−(x/L))(dv/dt)−(v^2 /L)=(T/m) ...(i) (d/dt)(Mv)=Mg−T M(dv/dt)+(m/L)v^2 =Mg−T (1+(x/L))(dv/dt)+(v^2 /L)=(1+(x/L))g−(T/m) ...(ii) (i)+(ii): ((3/2)−(x/L))(dv/dt)−(v^2 /L)+(1+(x/L))(dv/dt)+(v^2 /L)=(1+(x/L))g (dv/dt)=((2g)/5)(1+(x/L)) v(dv/dx)=((2g)/5)(1+(x/L)) vdv=((2g)/5)(1+(x/L))dx ∫_0 ^v vdv=((2g)/5)∫_0 ^x (1+(x/L))dx v^2 =((2g)/5)(2+(x/L))x ⇒v(x)=(√(((2gL)/5)(2+(x/L))((x/L)))) v_1 =v(L)=(√((6gL)/5)) ================== (dx/dt)=(√(((2gL)/5)(2+(x/L))((x/L)))) (d/dt)((x/L))=(√(((2g)/(5L))(2+(x/L))((x/L)))) (dξ/dt)=(√(((2g)/(5L))(2+ξ)ξ)) (√((5L)/(2g)))(dξ/( (√((2+ξ)ξ))))=dt (√((5L)/(2g)))∫_0 ^ξ (dξ/( (√((2+ξ)ξ))))=∫_0 ^t dt (√((5L)/(2g)))[2ln ((√(2+ξ))+(√ξ))]_0 ^ξ =t ⇒t(x)=(√((10L)/g))ln (((√(2+(x/L)))+(√(x/L)))/( (√2))) t_1 =t(L)=(√((10L)/g))ln (((√3)+1)/( (√2)))](Q158877.png)
Commented by ajfour last updated on 09/Nov/21

Commented by mr W last updated on 10/Nov/21
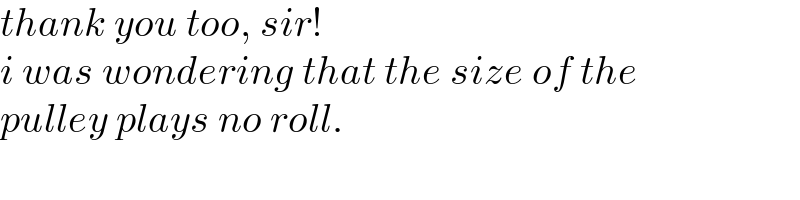
Commented by ajfour last updated on 10/Nov/21

Commented by Tawa11 last updated on 10/Nov/21

Answered by ajfour last updated on 09/Nov/21