
Question and Answers Forum
Question Number 168745 by MikeH last updated on 17/Apr/22
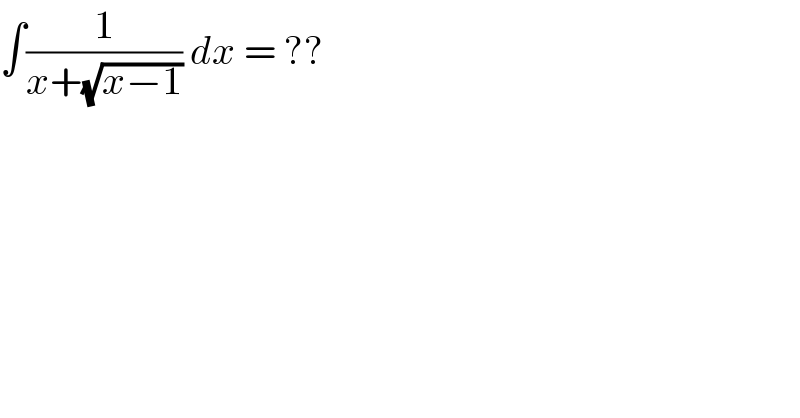
Commented by safojontoshtemirov last updated on 17/Apr/22
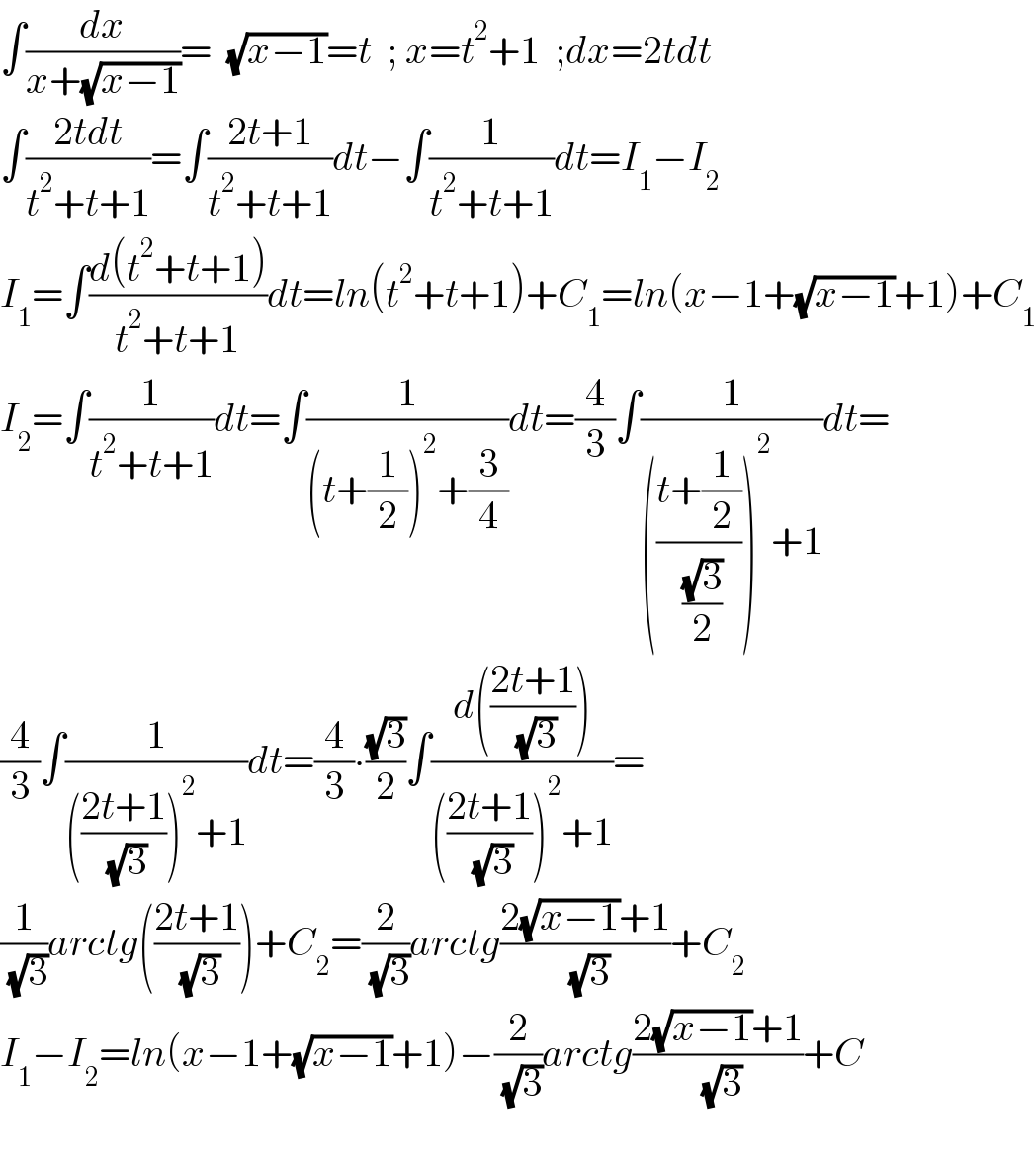
Answered by blackmamba last updated on 17/Apr/22
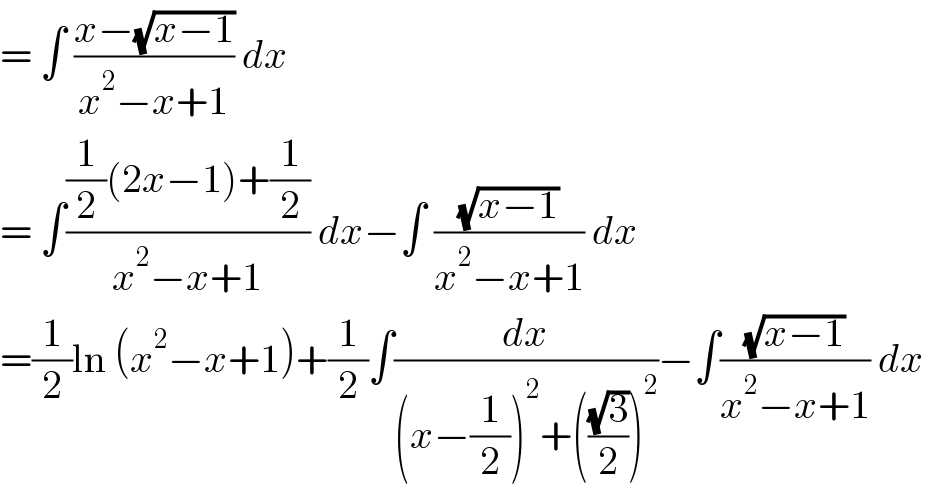
| ||
Question and Answers Forum | ||
Question Number 168745 by MikeH last updated on 17/Apr/22 | ||
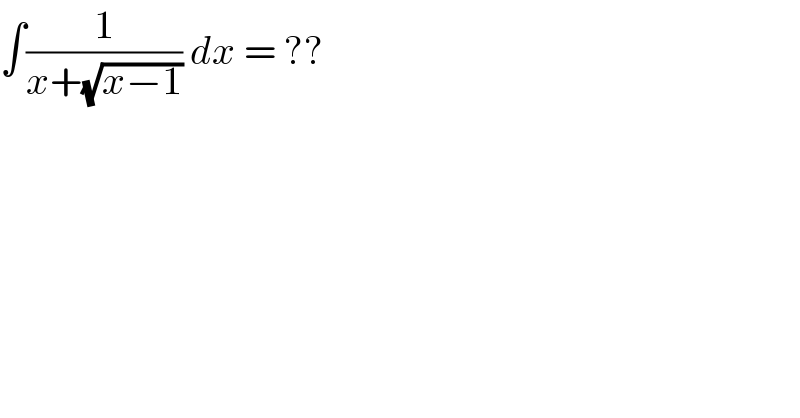 | ||
Commented by safojontoshtemirov last updated on 17/Apr/22 | ||
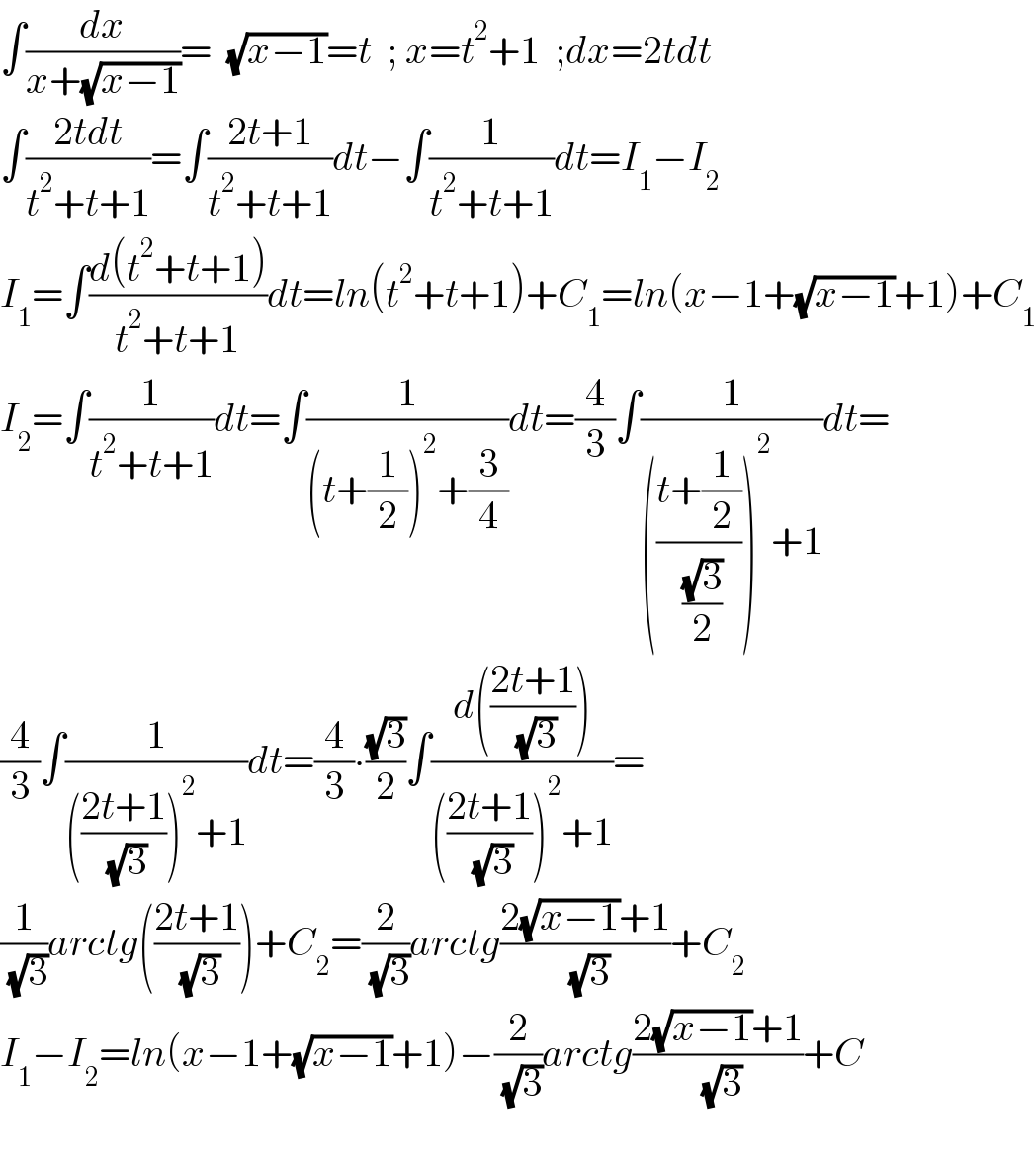 | ||
Answered by blackmamba last updated on 17/Apr/22 | ||
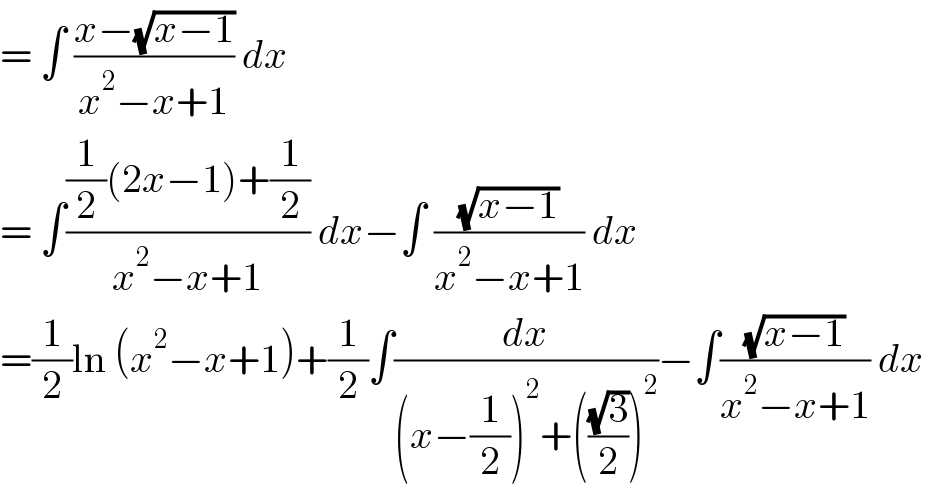 | ||
| ||