
Question and Answers Forum
Question Number 1594 by 123456 last updated on 24/Aug/15
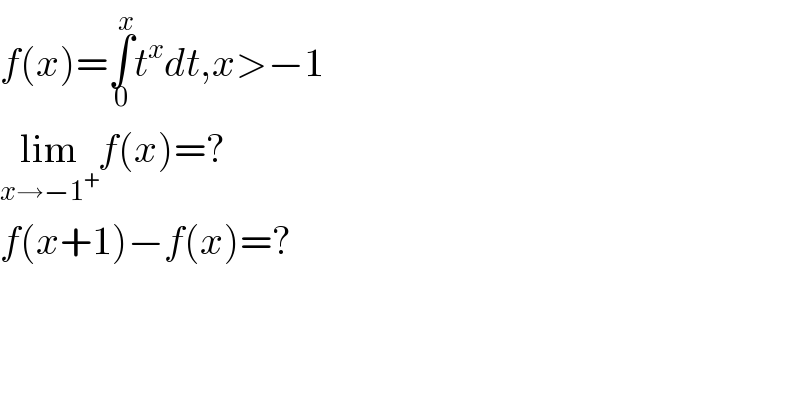
Commented by112358 last updated on 25/Aug/15
![f(x)=∫_0 ^x t^x dt=(t^(x+1) /(x+1))∣_0 ^x =(1/(x+1))(x^(x+1) −0^(x+1) ) f(x)=(1/(x+1))x^(x+1) ,x>−1 f(x+1)−f(x)=(1/(x+2))(x+1)^(x+2) −(1/(x+1))x^(x+1) rhs=(((x+1)^2 )/(x+2))(x+1)^x −(x/(x+1))x^x =((x^2 +2x+1)/(x+2))(x+1)^x −(x/(x+1))x^x =((x(x+2)+1)/(x+2))(x+1)^x −(x/(x+1))x^x =x[(x+1)^x −(x^x /(x+1))]+(((x+1)^x )/(x+2)) =x[(((x+1)^(x+1) −x^x )/(x+1))]+(((x+1)^x )/(x+2)) =((x{(x+1)^(x+1) −x^x }(x+2)+(x+1)^(x+1) )/((x+1)(x+2))) =((x^2 (x+1)^(x+1) +2x(x+1)^(x+1) +(x+1)^(x+1) −x^(x+2) −2x^(x+1) )/((x+1)(x+2))) f(x+1)−f(x)=(((x+1)^(x+3) −x^(x+1) (x+2))/((x+1)(x+2))) f(x)=(1/(1+x))x^(x+1) =(x/(1+x))x^x =(1−(1/(x+1)))x^x Let L=lim_(x→−1^+ ) f(x) (if this limit exists) L=lim_(x→−1^+ ) f(x)=lim_(x→−1^+ ) [(1−(1/(x+1)))x^x ] L=[lim_(x→−1^+ ) (1−(1/(x+1)))]×[lim_(x→−1^+ ) x^x ] Let p=lim_(x→−1^+ ) x^x p=lim_(x→−1^+ ) x^x =lim_(x→−1^+ ) e^(lnx^x ) =lim_(x→−1^+ ) e^(xlnx) p=e^(lim_(x→−1^+ ) xlnx) =e^((lim_(x→−1^+ ) x)(lim_(x→−1^+ ) lnx)) p=e^(−1×ln(−1)) =e^(ln(−1)) =e^(ln1+iπ) p=e^(iπ) =−1 Let q=lim_(x→−1^+ ) (1−(1/(x+1))) (1/(1+x))=(1+x)^(−1) ⇒ (1/(1+x))=e^(−ln(x+1)) ∴q=lim_(x→−1^+ ) 1−exp(−lim_(x→−1^+ ) ln(x+1)) Now, lim_(x→−1^+ ) ln(x+1)=−∞ ∴ q=1−exp(−1×−∞)=−∞ ∵ L=p×q⇒L=−∞×−1=∞ L does not exist. ⇒lim_(x→−1^+ ) f(x) does not exist](Q1595.png)
Commented byRasheed Soomro last updated on 24/Aug/15

| ||
Question and Answers Forum | ||
Question Number 1594 by 123456 last updated on 24/Aug/15 | ||
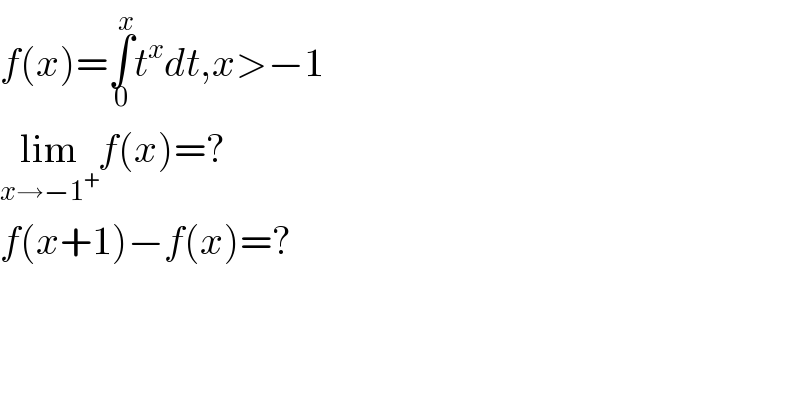 | ||
Commented by112358 last updated on 25/Aug/15 | ||
![f(x)=∫_0 ^x t^x dt=(t^(x+1) /(x+1))∣_0 ^x =(1/(x+1))(x^(x+1) −0^(x+1) ) f(x)=(1/(x+1))x^(x+1) ,x>−1 f(x+1)−f(x)=(1/(x+2))(x+1)^(x+2) −(1/(x+1))x^(x+1) rhs=(((x+1)^2 )/(x+2))(x+1)^x −(x/(x+1))x^x =((x^2 +2x+1)/(x+2))(x+1)^x −(x/(x+1))x^x =((x(x+2)+1)/(x+2))(x+1)^x −(x/(x+1))x^x =x[(x+1)^x −(x^x /(x+1))]+(((x+1)^x )/(x+2)) =x[(((x+1)^(x+1) −x^x )/(x+1))]+(((x+1)^x )/(x+2)) =((x{(x+1)^(x+1) −x^x }(x+2)+(x+1)^(x+1) )/((x+1)(x+2))) =((x^2 (x+1)^(x+1) +2x(x+1)^(x+1) +(x+1)^(x+1) −x^(x+2) −2x^(x+1) )/((x+1)(x+2))) f(x+1)−f(x)=(((x+1)^(x+3) −x^(x+1) (x+2))/((x+1)(x+2))) f(x)=(1/(1+x))x^(x+1) =(x/(1+x))x^x =(1−(1/(x+1)))x^x Let L=lim_(x→−1^+ ) f(x) (if this limit exists) L=lim_(x→−1^+ ) f(x)=lim_(x→−1^+ ) [(1−(1/(x+1)))x^x ] L=[lim_(x→−1^+ ) (1−(1/(x+1)))]×[lim_(x→−1^+ ) x^x ] Let p=lim_(x→−1^+ ) x^x p=lim_(x→−1^+ ) x^x =lim_(x→−1^+ ) e^(lnx^x ) =lim_(x→−1^+ ) e^(xlnx) p=e^(lim_(x→−1^+ ) xlnx) =e^((lim_(x→−1^+ ) x)(lim_(x→−1^+ ) lnx)) p=e^(−1×ln(−1)) =e^(ln(−1)) =e^(ln1+iπ) p=e^(iπ) =−1 Let q=lim_(x→−1^+ ) (1−(1/(x+1))) (1/(1+x))=(1+x)^(−1) ⇒ (1/(1+x))=e^(−ln(x+1)) ∴q=lim_(x→−1^+ ) 1−exp(−lim_(x→−1^+ ) ln(x+1)) Now, lim_(x→−1^+ ) ln(x+1)=−∞ ∴ q=1−exp(−1×−∞)=−∞ ∵ L=p×q⇒L=−∞×−1=∞ L does not exist. ⇒lim_(x→−1^+ ) f(x) does not exist](Q1595.png) | ||
Commented byRasheed Soomro last updated on 24/Aug/15 | ||
 | ||