
Question Number 160009 by HongKing last updated on 23/Nov/21
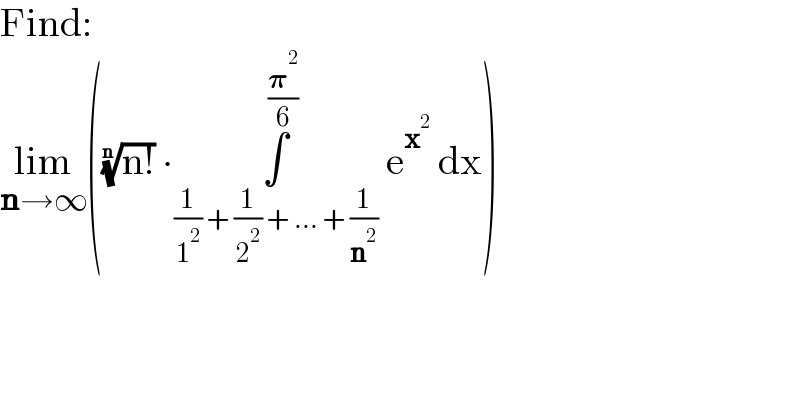
$$\mathrm{Find}: \\ $$$$\underset{\boldsymbol{\mathrm{n}}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt[{\boldsymbol{\mathrm{n}}}]{\mathrm{n}!}\:\centerdot\underset{\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\:...\:+\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }} {\overset{\:\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{6}}} {\int}}\:\mathrm{e}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \:\mathrm{dx}\right) \\ $$
Answered by Tokugami last updated on 23/Nov/21
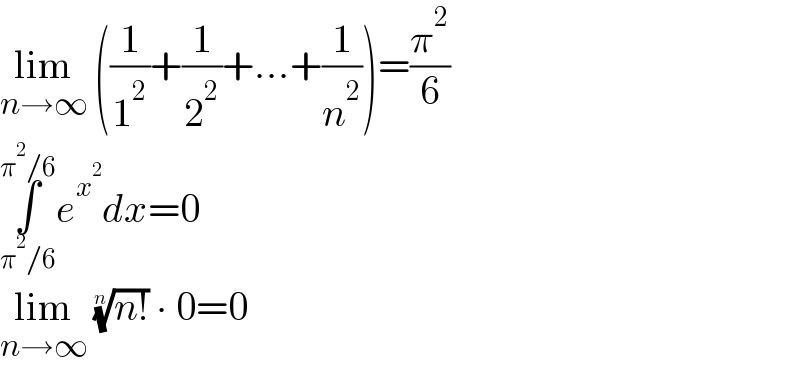
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+...+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\underset{\pi^{\mathrm{2}} /\mathrm{6}} {\overset{\pi^{\mathrm{2}} /\mathrm{6}} {\int}}{e}^{{x}^{\mathrm{2}} } {dx}=\mathrm{0} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{{n}}]{{n}!}\:\centerdot\:\mathrm{0}=\mathrm{0} \\ $$
Commented by kowalsky78 last updated on 23/Nov/21
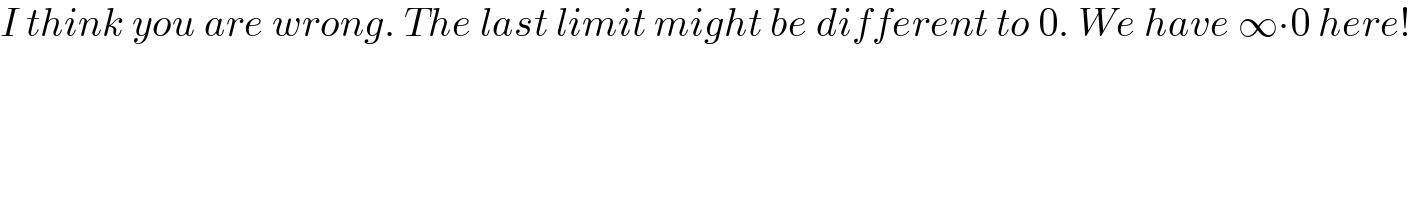
$${I}\:{think}\:{you}\:{are}\:{wrong}.\:{The}\:{last}\:{limit}\:{might}\:{be}\:{different}\:{to}\:\mathrm{0}.\:{We}\:{have}\:\infty\centerdot\mathrm{0}\:{here}! \\ $$$$\: \\ $$
Commented by HongKing last updated on 23/Nov/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Ser} \\ $$$$\mathrm{but}\:\mathrm{answer}:\:\mathrm{e}^{\frac{\boldsymbol{\pi}^{\mathrm{4}} -\mathrm{36}}{\mathrm{36}}} \\ $$
