Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 160091 by abdullah_ff last updated on 24/Nov/21

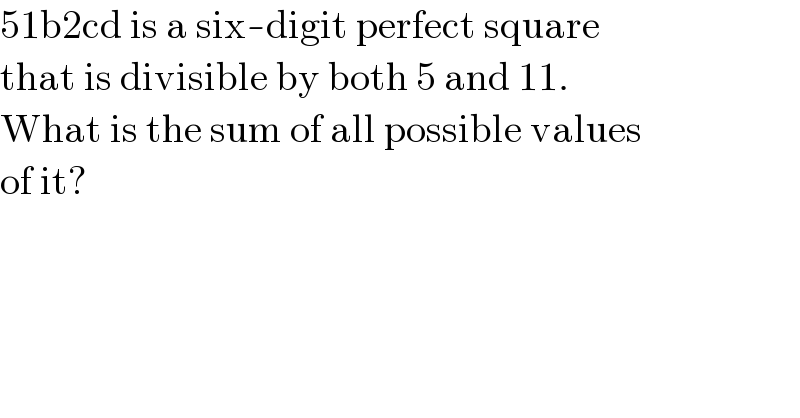
51b2cd is a six-digit perfect square that is divisible by both 5 and 11. What is the sum of all possible values of it?

$$\mathrm{51b2cd}\:\mathrm{is}\:\mathrm{a}\:\mathrm{six}-\mathrm{digit}\:\mathrm{perfect}\:\mathrm{square}\: \\ $$$$\mathrm{that}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{both}\:\mathrm{5}\:\mathrm{and}\:\mathrm{11}.\: \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{values}\: \\ $$$$\mathrm{of}\:\mathrm{it}? \\ $$

Commented by Rasheed.Sindhi last updated on 24/Nov/21

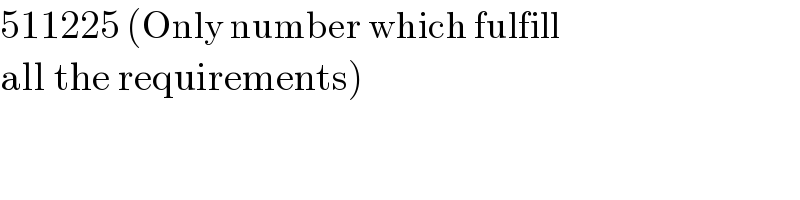
511225 (Only number which fulfill all the requirements)

$$\mathrm{511225}\:\left(\mathrm{Only}\:\mathrm{number}\:\mathrm{which}\:\mathrm{fulfill}\right. \\ $$$$\left.\mathrm{all}\:\mathrm{the}\:\mathrm{requirements}\right) \\ $$

Answered by Rasheed.Sindhi last updated on 24/Nov/21

▶5 ∣ 51b2cd ∧ 11 ∣ 51b2cd ∧ (51b2cd is perfect-square) ⇒25 ∣ 51b2cd ∧ 121∣ 51b2cd ⇒25×121=3025 ∣ 51b2cd ⇒3025m^2 =51b2cd m should be replaced so that 3025m^2 has leading two digits ′51′ and 4th digit from left is 2. So m=13 3025×13^2 =511225. No other number can fulfill all these requirements. Sum of all possible such numbers =511225 (∵ there′s only single number)

$$\:\blacktriangleright\mathrm{5}\:\mid\:\mathrm{51b2cd}\:\:\wedge\:\:\mathrm{11}\:\mid\:\mathrm{51b2cd}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\wedge\:\left(\mathrm{51b2cd}\:\mathrm{is}\:\mathrm{perfect}-\mathrm{square}\right) \\ $$$$\Rightarrow\mathrm{25}\:\mid\:\mathrm{51b2cd}\:\wedge\:\mathrm{121}\mid\:\mathrm{51b2cd} \\ $$$$\Rightarrow\mathrm{25}×\mathrm{121}=\mathrm{3025}\:\mid\:\mathrm{51b2cd} \\ $$$$\Rightarrow\mathrm{3025m}^{\mathrm{2}} =\mathrm{51b2cd} \\ $$$$\mathrm{m}\:\mathrm{should}\:\mathrm{be}\:\mathrm{replaced}\:\mathrm{so}\:\mathrm{that}\:\mathrm{3025m}^{\mathrm{2}} \\ $$$$\mathrm{has}\:\mathrm{leading}\:\mathrm{two}\:\mathrm{digits}\:'\mathrm{51}'\:\mathrm{and}\:\mathrm{4th} \\ $$$$\mathrm{digit}\:\mathrm{from}\:\mathrm{left}\:\mathrm{is}\:\mathrm{2}.\:\mathrm{So}\:\mathrm{m}=\mathrm{13} \\ $$$$\mathrm{3025}×\mathrm{13}^{\mathrm{2}} =\mathrm{511225}. \\ $$$$\mathrm{No}\:\mathrm{other}\:\mathrm{number}\:\mathrm{can}\:\mathrm{fulfill}\:\mathrm{all}\:\mathrm{these} \\ $$$$\mathrm{requirements}. \\ $$$$\mathrm{Sum}\:\mathrm{of}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{such}\:\mathrm{numbers} \\ $$$$=\mathrm{511225}\:\left(\because\:\mathrm{there}'\mathrm{s}\:\mathrm{only}\:\mathrm{single}\:\mathrm{number}\right) \\ $$

Commented by abdullah_ff last updated on 24/Nov/21

good way sir. many many thanks

$${good}\:{way}\:{sir}.\:{many}\:{many}\:{thanks} \\ $$

Answered by mr W last updated on 25/Nov/21

let 51b2cd=n^2 510200≤n^2 ≤519299 (√(510200))≤n≤(√(519299)) ⇒715≤n≤720 since the number is divisible by 5, the last digit of n^2 must be 5 or 0. there are only two possibilities: n=715 or 720 with n=715: 715^2 =511225≡0 mod 11 (✓) with n=720: 720^2 =518400≢0 mod 11 (×) so we have only 511225 as solution.

$${let}\:\mathrm{51}{b}\mathrm{2}{cd}={n}^{\mathrm{2}} \\ $$$$\mathrm{510200}\leqslant{n}^{\mathrm{2}} \leqslant\mathrm{519299} \\ $$$$\sqrt{\mathrm{510200}}\leqslant{n}\leqslant\sqrt{\mathrm{519299}} \\ $$$$\Rightarrow\mathrm{715}\leqslant{n}\leqslant\mathrm{720} \\ $$$${since}\:{the}\:{number}\:{is}\:{divisible}\:{by}\:\mathrm{5}, \\ $$$${the}\:{last}\:{digit}\:{of}\:{n}^{\mathrm{2}} \:{must}\:{be}\:\mathrm{5}\:{or}\:\mathrm{0}. \\ $$$${there}\:{are}\:{only}\:{two}\:{possibilities}:\: \\ $$$${n}=\mathrm{715}\:{or}\:\mathrm{720} \\ $$$$\underline{{with}\:{n}=\mathrm{715}:} \\ $$$$\mathrm{715}^{\mathrm{2}} =\mathrm{511225}\equiv\mathrm{0}\:{mod}\:\mathrm{11}\:\left(\checkmark\right) \\ $$$$\underline{{with}\:{n}=\mathrm{720}:} \\ $$$$\mathrm{720}^{\mathrm{2}} =\mathrm{518400}≢\mathrm{0}\:{mod}\:\mathrm{11}\:\left(×\right) \\ $$$${so}\:{we}\:{have}\:{only}\:\mathrm{511225}\:{as}\:{solution}. \\ $$

Commented by abdullah_ff last updated on 25/Nov/21

thank you very much sir.

$${thank}\:{you}\:{very}\:{much}\:{sir}. \\ $$

Commented by Rasheed.Sindhi last updated on 25/Nov/21

More efficient approach!

$$\mathrm{More}\:\mathrm{efficient}\:\mathrm{approach}! \\ $$

Answered by Rasheed.Sindhi last updated on 25/Nov/21

▶ ∵51b2cd is perfect square & 5 ∣ 51b2cd ∴25 ∣ 51b2cd ∴ cd=00 ∨ cd=25 (xxxx50 and xxxx75 aren′t perfect squares) cd=00⇒51b2cd=51b200=51b2×100 ⇒51b2 shoud be perfect square but it can′t be due to 2 at unit place. ∴ cd=00 (×) & cd=25 (✓) ▶ 11 ∣ 51b2cd⇒ (5+b+c)−(1+2+d)=0,11... ⇒(5+b+2)−(1+2+5)=0,11,... ⇒b−1=0,11⇒b=1,12,... ∵ b is decimal digit ∴ b=1 ∴ 51b2cd=511225

$$\blacktriangleright \\ $$$$\because\mathrm{51b2cd}\:\mathrm{is}\:\mathrm{perfect}\:\mathrm{square}\:\&\:\mathrm{5}\:\mid\:\mathrm{51b2cd} \\ $$$$\therefore\mathrm{25}\:\mid\:\mathrm{51b2cd} \\ $$$$\therefore\:\mathrm{cd}=\mathrm{00}\:\vee\:\mathrm{cd}=\mathrm{25}\: \\ $$$$\left(\mathrm{xxxx50}\:\mathrm{and}\:\mathrm{xxxx75}\:\mathrm{aren}'\mathrm{t}\:\mathrm{perfect}\:\mathrm{squares}\right) \\ $$$$\mathrm{cd}=\mathrm{00}\Rightarrow\mathrm{51b2cd}=\mathrm{51b200}=\mathrm{51b2}×\mathrm{100} \\ $$$$\Rightarrow\mathrm{51b2}\:\mathrm{shoud}\:\mathrm{be}\:\mathrm{perfect}\:\mathrm{square}\:\mathrm{but} \\ $$$$\:\:\:\:\:\:\mathrm{it}\:\mathrm{can}'\mathrm{t}\:\mathrm{be}\:\mathrm{due}\:\mathrm{to}\:\mathrm{2}\:\mathrm{at}\:\mathrm{unit}\:\mathrm{place}. \\ $$$$\therefore\:\mathrm{cd}=\mathrm{00}\:\left(×\right)\:\:\&\:\:\mathrm{cd}=\mathrm{25}\:\left(\checkmark\right) \\ $$$$\blacktriangleright \\ $$$$\:\mathrm{11}\:\mid\:\mathrm{51b2cd}\Rightarrow\:\left(\mathrm{5}+\mathrm{b}+\mathrm{c}\right)−\left(\mathrm{1}+\mathrm{2}+\mathrm{d}\right)=\mathrm{0},\mathrm{11}... \\ $$$$\Rightarrow\left(\mathrm{5}+\mathrm{b}+\mathrm{2}\right)−\left(\mathrm{1}+\mathrm{2}+\mathrm{5}\right)=\mathrm{0},\mathrm{11},... \\ $$$$\Rightarrow\mathrm{b}−\mathrm{1}=\mathrm{0},\mathrm{11}\Rightarrow\mathrm{b}=\mathrm{1},\mathrm{12},... \\ $$$$\because\:\mathrm{b}\:\mathrm{is}\:\mathrm{decimal}\:\mathrm{digit}\:\therefore\:\mathrm{b}=\mathrm{1} \\ $$$$\therefore\:\mathrm{51b2cd}=\mathrm{511225} \\ $$

Commented by abdullah_ff last updated on 25/Nov/21

thanks!

$${thanks}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com