Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 160358 by Ar Brandon last updated on 28/Nov/21

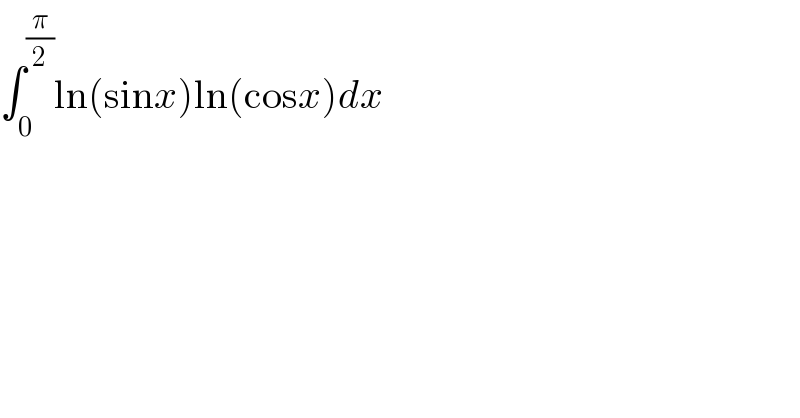
∫_0 ^(π/2) ln(sinx)ln(cosx)dx

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{x}\right)\mathrm{ln}\left(\mathrm{cos}{x}\right){dx} \\ $$

Answered by amin96 last updated on 28/Nov/21

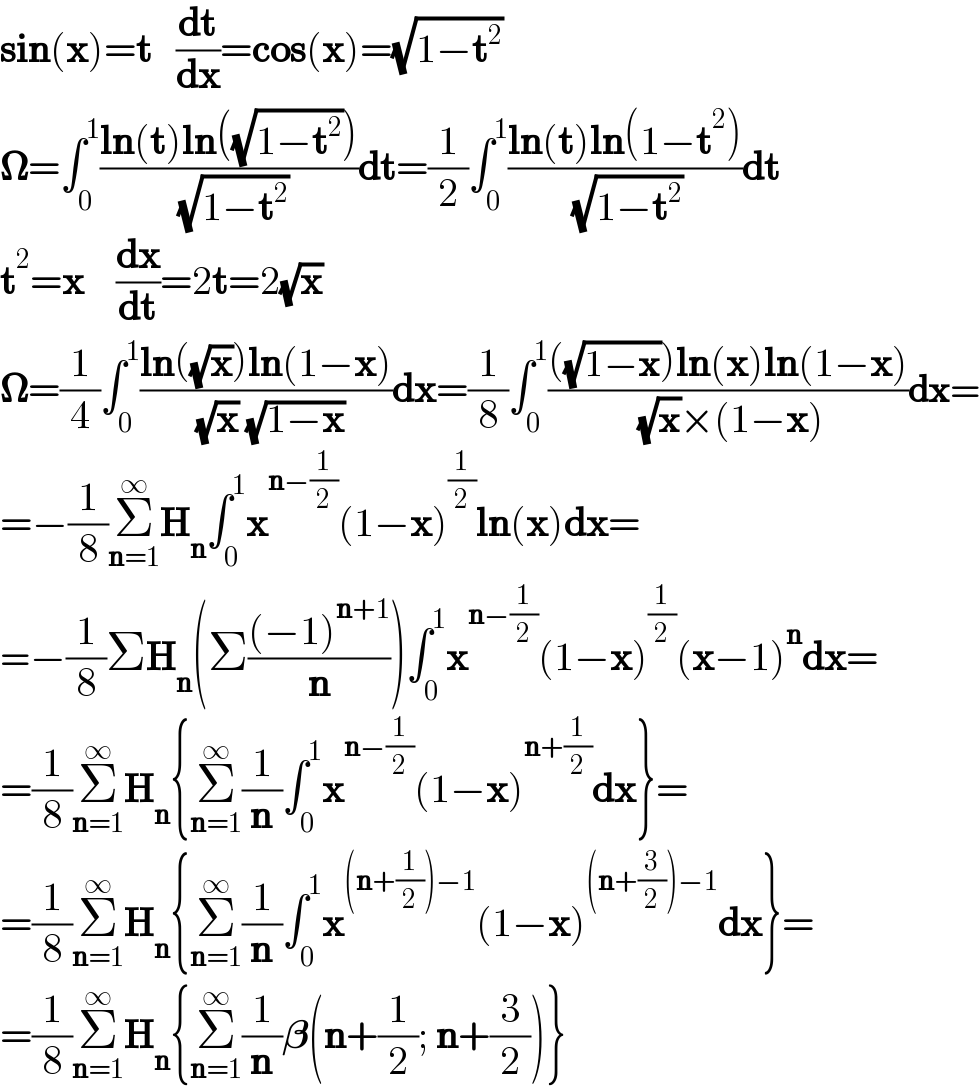
sin(x)=t (dt/dx)=cos(x)=(√(1−t^2 )) 𝛀=∫_0 ^1 ((ln(t)ln((√(1−t^2 ))))/( (√(1−t^2 ))))dt=(1/2)∫_0 ^1 ((ln(t)ln(1−t^2 ))/( (√(1−t^2 ))))dt t^2 =x (dx/dt)=2t=2(√x) 𝛀=(1/4)∫_0 ^1 ((ln((√x))ln(1−x))/( (√x) (√(1−x))))dx=(1/8)∫_0 ^1 ((((√(1−x)))ln(x)ln(1−x))/( (√x)×(1−x)))dx= =−(1/8)Σ_(n=1) ^∞ H_n ∫_0 ^1 x^(n−(1/2)) (1−x)^(1/2) ln(x)dx= =−(1/8)ΣH_n (Σ(((−1)^(n+1) )/n))∫_0 ^1 x^(n−(1/2)) (1−x)^(1/2) (x−1)^n dx= =(1/8)Σ_(n=1) ^∞ H_n {Σ_(n=1) ^∞ (1/n)∫_0 ^1 x^(n−(1/2)) (1−x)^(n+(1/2)) dx}= =(1/8)Σ_(n=1) ^∞ H_n {Σ_(n=1) ^∞ (1/n)∫_0 ^1 x^((n+(1/2))−1) (1−x)^((n+(3/2))−1) dx}= =(1/8)Σ_(n=1) ^∞ H_n {Σ_(n=1) ^∞ (1/n)𝛃(n+(1/2); n+(3/2))}

$$\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)=\boldsymbol{\mathrm{t}}\:\:\:\frac{\boldsymbol{\mathrm{dt}}}{\boldsymbol{\mathrm{dx}}}=\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)=\sqrt{\mathrm{1}−\boldsymbol{\mathrm{t}}^{\mathrm{2}} } \\ $$$$\boldsymbol{\Omega}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{t}}\right)\boldsymbol{\mathrm{ln}}\left(\sqrt{\mathrm{1}−\boldsymbol{\mathrm{t}}^{\mathrm{2}} }\right)}{\:\sqrt{\mathrm{1}−\boldsymbol{\mathrm{t}}^{\mathrm{2}} }}\boldsymbol{\mathrm{dt}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{t}}\right)\boldsymbol{\mathrm{ln}}\left(\mathrm{1}−\boldsymbol{\mathrm{t}}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}−\boldsymbol{\mathrm{t}}^{\mathrm{2}} }}\boldsymbol{\mathrm{dt}} \\ $$$$\boldsymbol{\mathrm{t}}^{\mathrm{2}} =\boldsymbol{\mathrm{x}}\:\:\:\:\frac{\boldsymbol{\mathrm{dx}}}{\boldsymbol{\mathrm{dt}}}=\mathrm{2}\boldsymbol{\mathrm{t}}=\mathrm{2}\sqrt{\boldsymbol{\mathrm{x}}}\:\:\: \\ $$$$\boldsymbol{\Omega}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{ln}}\left(\sqrt{\boldsymbol{\mathrm{x}}}\right)\boldsymbol{\mathrm{ln}}\left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)}{\:\sqrt{\boldsymbol{\mathrm{x}}}\:\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}}}\boldsymbol{\mathrm{dx}}=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}}\right)\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{ln}}\left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)}{\:\sqrt{\boldsymbol{\mathrm{x}}}×\left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)}\boldsymbol{\mathrm{dx}}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\boldsymbol{\mathrm{H}}_{\boldsymbol{\mathrm{n}}} \int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{dx}}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}}\Sigma\boldsymbol{\mathrm{H}}_{\boldsymbol{\mathrm{n}}} \left(\Sigma\frac{\left(−\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}+\mathrm{1}} }{\boldsymbol{\mathrm{n}}}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}} \boldsymbol{\mathrm{dx}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\boldsymbol{\mathrm{H}}_{\boldsymbol{\mathrm{n}}} \left\{\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)^{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{\mathrm{dx}}\right\}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\boldsymbol{\mathrm{H}}_{\boldsymbol{\mathrm{n}}} \left\{\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{x}}^{\left(\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}} \left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)^{\left(\boldsymbol{\mathrm{n}}+\frac{\mathrm{3}}{\mathrm{2}}\right)−\mathrm{1}} \boldsymbol{\mathrm{dx}}\right\}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\boldsymbol{\mathrm{H}}_{\boldsymbol{\mathrm{n}}} \left\{\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}\boldsymbol{\beta}\left(\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}};\:\boldsymbol{\mathrm{n}}+\frac{\mathrm{3}}{\mathrm{2}}\right)\right\} \\ $$

Commented by Ar Brandon last updated on 28/Nov/21

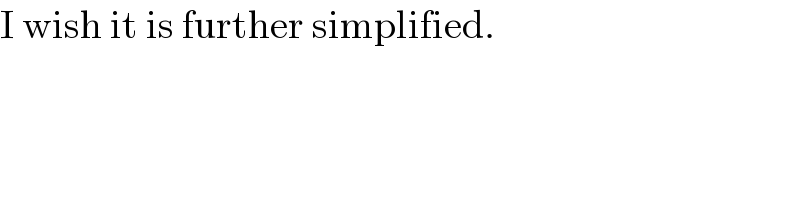
I wish it is further simplified.

$$\mathrm{I}\:\mathrm{wish}\:\mathrm{it}\:\mathrm{is}\:\mathrm{further}\:\mathrm{simplified}. \\ $$

Commented by amin96 last updated on 28/Nov/21

do you know the answer?

$$ \\ $$ do you know the answer?

Commented by Ar Brandon last updated on 29/Nov/21

Yeah

$$\mathrm{Yeah} \\ $$

Commented by Ar Brandon last updated on 29/Nov/21

(π/2)ln^2 2−(π^3 /(48))

$$\frac{\pi}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \mathrm{2}−\frac{\pi^{\mathrm{3}} }{\mathrm{48}} \\ $$

Commented by amin96 last updated on 29/Nov/21

∫_0 ^(π/2) xln(sinx)ln(cosx)dx The answer to this integral

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \boldsymbol{\mathrm{xln}}\left(\boldsymbol{\mathrm{sinx}}\right)\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{cosx}}\right)\boldsymbol{\mathrm{dx}}\: \\ $$$$ \\ $$The answer to this integral

Commented by Ar Brandon last updated on 29/Nov/21

∫_0 ^(π/2) xln(sinx)ln(cosx)dx=(π^2 /8)ln^2 2−(π^4 /(192)) ∫_0 ^(π/2) xln(sinx)ln(cosx)dx=(π/4)∫_0 ^(π/2) ln(sinx)ln(cosx)dx

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}\mathrm{ln}\left(\mathrm{sin}{x}\right)\mathrm{ln}\left(\mathrm{cos}{x}\right){dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\mathrm{ln}^{\mathrm{2}} \mathrm{2}−\frac{\pi^{\mathrm{4}} }{\mathrm{192}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}\mathrm{ln}\left(\mathrm{sin}{x}\right)\mathrm{ln}\left(\mathrm{cos}{x}\right){dx}=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{x}\right)\mathrm{ln}\left(\mathrm{cos}{x}\right){dx} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com