Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 160444 by HongKing last updated on 29/Nov/21

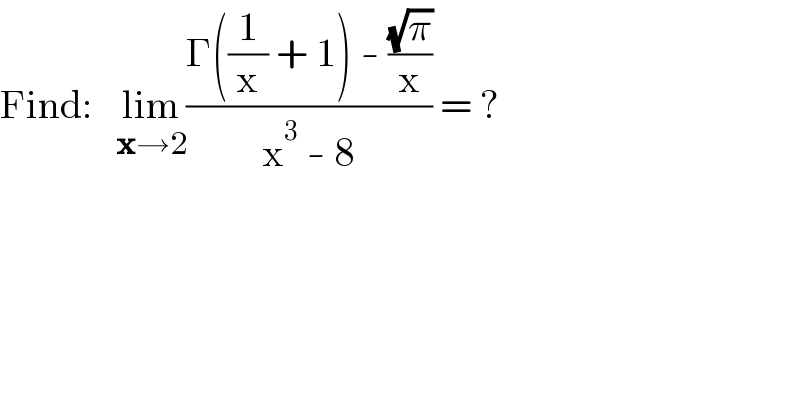
Find: lim_(x→2) ((Γ((1/x) + 1) - ((√π)/x))/(x^3 - 8)) = ?

$$\mathrm{Find}:\:\:\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{x}}\:+\:\mathrm{1}\right)\:-\:\frac{\sqrt{\pi}}{\mathrm{x}}}{\mathrm{x}^{\mathrm{3}} \:-\:\mathrm{8}}\:=\:? \\ $$

Answered by Ar Brandon last updated on 29/Nov/21

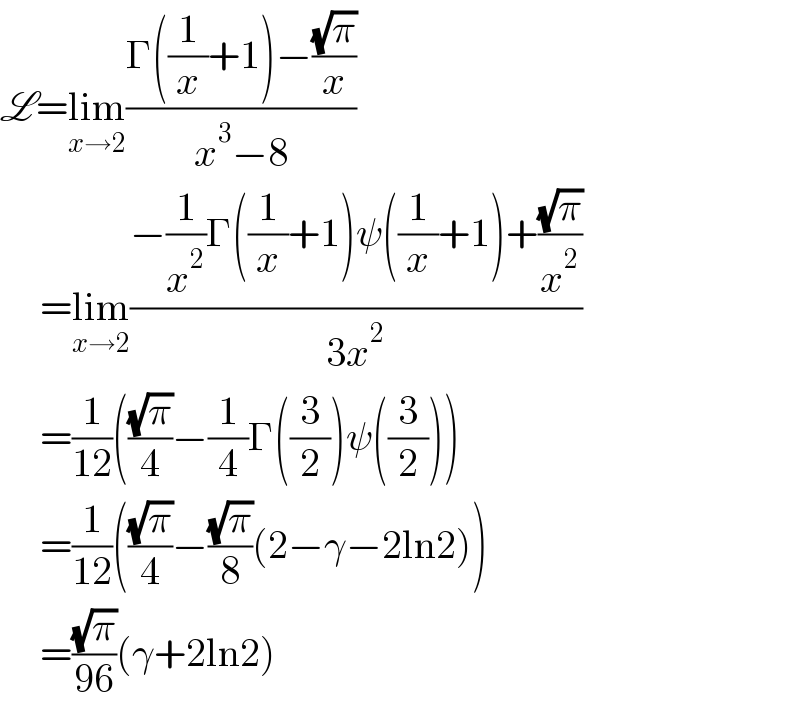
L=lim_(x→2) ((Γ((1/x)+1)−((√π)/x))/(x^3 −8)) =lim_(x→2) ((−(1/x^2 )Γ((1/x)+1)ψ((1/x)+1)+((√π)/x^2 ))/(3x^2 )) =(1/(12))(((√π)/4)−(1/4)Γ((3/2))ψ((3/2))) =(1/(12))(((√π)/4)−((√π)/8)(2−γ−2ln2)) =((√π)/(96))(γ+2ln2)

$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\Gamma\left(\frac{\mathrm{1}}{{x}}+\mathrm{1}\right)−\frac{\sqrt{\pi}}{{x}}}{{x}^{\mathrm{3}} −\mathrm{8}} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\Gamma\left(\frac{\mathrm{1}}{{x}}+\mathrm{1}\right)\psi\left(\frac{\mathrm{1}}{{x}}+\mathrm{1}\right)+\frac{\sqrt{\pi}}{{x}^{\mathrm{2}} }}{\mathrm{3}{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{12}}\left(\frac{\sqrt{\pi}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{12}}\left(\frac{\sqrt{\pi}}{\mathrm{4}}−\frac{\sqrt{\pi}}{\mathrm{8}}\left(\mathrm{2}−\gamma−\mathrm{2ln2}\right)\right) \\ $$$$\:\:\:\:\:=\frac{\sqrt{\pi}}{\mathrm{96}}\left(\gamma+\mathrm{2ln2}\right) \\ $$

Commented by HongKing last updated on 29/Nov/21

perfect my dear Sir thank you so much

$$\mathrm{perfect}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Answered by mnjuly1970 last updated on 30/Nov/21

−−−−−−−− solution L :=_(rule) ^(Hopital′s) lim_( x→ 2) ((((−1)/x^( 2) ) Γ ′(1+(1/x) )+((√π)/x^( 2) ))/(3x^( 2) )) := lim_( x→2) (((√π) −Γ′(1+(1/x) ))/(3x^( 4) )) ∴ L:= (( (√π) −Γ′ ((3/2)))/(48)) = (((√π) −ψ ((3/2) )Γ((3/2)))/(48)) =(((√π) −(1/2)( 2−γ−ln(4)).(√π))/(48)) L := (((√π) ( γ +ln(4) )/(96))

$$\:\:\:\:−−−−−−−− \\ $$$$\:\:\:\:\:{solution}\: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{L}\::\underset{\mathrm{rule}} {\overset{\mathrm{Hopital}'\mathrm{s}} {=}}\:{lim}_{\:{x}\rightarrow\:\mathrm{2}} \frac{\frac{−\mathrm{1}}{{x}^{\:\mathrm{2}} }\:\Gamma\:'\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\:\right)+\frac{\sqrt{\pi}}{{x}^{\:\mathrm{2}} }}{\mathrm{3}{x}^{\:\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\::=\:{lim}_{\:{x}\rightarrow\mathrm{2}} \:\:\frac{\sqrt{\pi}\:−\Gamma'\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\:\right)}{\mathrm{3}{x}^{\:\mathrm{4}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\therefore\:\:\:\:\:\:\mathrm{L}:=\:\frac{\:\sqrt{\pi}\:−\Gamma'\:\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{48}}\:=\:\frac{\sqrt{\pi}\:−\psi\:\left(\frac{\mathrm{3}}{\mathrm{2}}\:\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{48}}\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\pi}\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\:\mathrm{2}−\gamma−{ln}\left(\mathrm{4}\right)\right).\sqrt{\pi}}{\mathrm{48}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{L}\::=\:\frac{\sqrt{\pi}\:\left(\:\:\gamma\:+{ln}\left(\mathrm{4}\right)\:\right.}{\mathrm{96}} \\ $$$$\:\: \\ $$$$ \\ $$

Commented by HongKing last updated on 30/Nov/21

perfect my dear Ser thank you so much

$$\mathrm{perfect}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Ser}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Commented by mnjuly1970 last updated on 01/Dec/21

thank you so much for your nice questions ..sir HongKing

$${thank}\:{you}\:{so}\:{much}\:{for}\:{your} \\ $$$$\:{nice}\:{questions}\:..{sir}\:\:\mathrm{H}{ong}\mathrm{K}{ing} \\ $$

Commented by HongKing last updated on 01/Dec/21

thank you my dear Sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{Sir}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com