Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 160596 by Ahmed1hamouda last updated on 03/Dec/21

Answered by Mathspace last updated on 03/Dec/21

$$I={\int }_c\frac{e^{3z}sin\left(2z\right)}{{(4z-j\pi )}^3}dzwithc\to \mid z-j\mid =1$$$$let\phi \left(z\right)=\frac{e^{3z}sin\left(2z\right)}{{(4z-j\pi )}^3}=\frac{e^{3z}sin\left(2z\right)}{64{(z-\frac{j\pi }{4})}^3}$$$$z=\frac{j\pi }{4}(itakej=e^{\frac{i2\pi }{3}})$$$$\mid \frac{j\pi }{4}-j\mid =\mid \frac{\pi }{4}-1\mid <1\Rightarrow$$$$I=2i\pi Res(\phi ,\frac{j\pi }{4})$$$$Res(\phi ,\frac{j\pi }{4})={lim}_{z\to \frac{j\pi }{4}}\frac{1}{(3-1)!}{\left\{{(z-\frac{j\pi }{4})}^3\phi \left(z\right)\right\}}^{\left(2\right)}$$$$={lim}_{z\to \frac{j\pi }{4}}\frac{1}{128}{\left\{e^{3z}sin\left(2z\right)\right\}}^{\left(2\right)}$$$$=\frac{1}{128}{lim}_{z\to \frac{j\pi }{4}}{\{3e^{3z}sin\left(2z\right)+2e^{3z}cos\left(2z\right)\}}^{\left(1\right)}$$$$=\frac{1}{128}{lim}_{z\to \frac{j\pi }{4}}(9e^{3z}sin\left(2z\right)+6e^{3z}cos\left(2z\right)+6e^{3z}cos\left(2z\right)-4e^{3z}sin\left(2z\right))$$$$=\frac{1}{128}\{9e^{\frac{3j\pi }{4}}sin\left(\frac{j\pi }{2}\right)+12e^{\frac{3j\pi }{4}}cos\left(\frac{j\pi }{2}\right)-4e^{\frac{3j\pi }{4}}sin\left(\frac{j\pi }{2}\right))$$

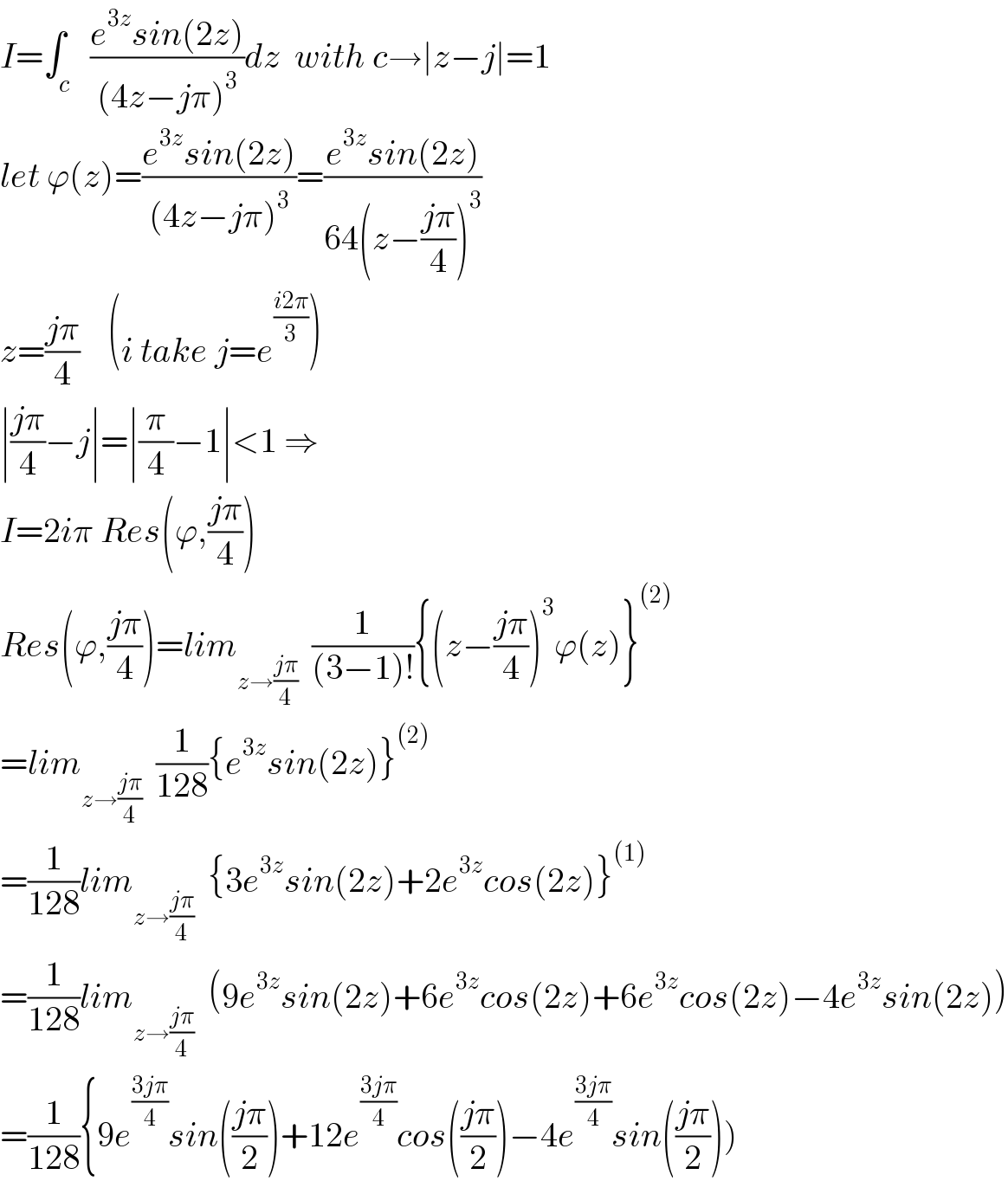
Commented by Ahmed1hamouda last updated on 03/Dec/21

In which reference engineering mathematics is there this issue

Commented by Mathspace last updated on 03/Dec/21

$$complexanalysisandtheoremofresidus$$

Commented by Ahmed1hamouda last updated on 03/Dec/21

What is the name of the author of this reference?

Terms of Service

Privacy Policy

Contact: info@tinkutara.com