
Question Number 16064 by Tinkutara last updated on 21/Jun/17
![Let ABCD be a convex quadrilateral and M a point in its interior such that [MAB] = [MBC] = [MCD] = [MDA]. Prove that one of the diagonals of ABCD passes through the midpoint of the other diagonal.](Q16064.png)
$$\mathrm{Let}\:{ABCD}\:\mathrm{be}\:\mathrm{a}\:\mathrm{convex}\:\mathrm{quadrilateral} \\ $$$$\mathrm{and}\:\mathrm{M}\:\mathrm{a}\:\mathrm{point}\:\mathrm{in}\:\mathrm{its}\:\mathrm{interior}\:\mathrm{such}\:\mathrm{that} \\ $$$$\left[{MAB}\right]\:=\:\left[{MBC}\right]\:=\:\left[{MCD}\right]\:=\:\left[{MDA}\right]. \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{diagonals}\:\mathrm{of} \\ $$$${ABCD}\:\mathrm{passes}\:\mathrm{through}\:\mathrm{the}\:\mathrm{midpoint}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{other}\:\mathrm{diagonal}. \\ $$
Commented by Tinkutara last updated on 20/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 24/Jun/17

$${Bo}×{oM}.{sin}\left({BoM}\right)={Do}×{oM}.{sin}\left(\mathrm{180}−{BoM}\right)\Rightarrow \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:{Bo}={Do}\Rightarrow\:{AC}\:\:{passes}\:{from}\:{midpoint} \\ $$$${of}\:{BD}. \\ $$
Commented by Tinkutara last updated on 27/Jun/17

$$\mathrm{This}\:\mathrm{is}\:\mathrm{incorrect}\:\mathrm{solution}.\:\mathrm{Should}\:\mathrm{I} \\ $$$$\mathrm{post}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{answer}? \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/Jun/17
![[BCM]=[CMD]⇒BM=MD [BMA]=[DMA]⇒∠BMA=∠DMA ⇒ { ((BM=MD)),((∠BMo=∠DMo)) :}⇒^(oM=oM) ΔBMo=ΔDMo ⇒Bo=Do⇒AC passes trough midpoint of BD.](Q16664.png)
$$\left[{BCM}\right]=\left[{CMD}\right]\Rightarrow{BM}={MD} \\ $$$$\left[{BMA}\right]=\left[{DMA}\right]\Rightarrow\angle{BMA}=\angle{DMA} \\ $$$$\Rightarrow\begin{cases}{{BM}={MD}}\\{\angle{BMo}=\angle{DMo}}\end{cases}\overset{{oM}={oM}} {\Rightarrow}\:\:\Delta{BMo}=\Delta{DMo} \\ $$$$\Rightarrow{Bo}={Do}\Rightarrow{AC}\:{passes}\:{trough}\:{midpoint} \\ $$$${of}\:{BD}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 27/Jun/17
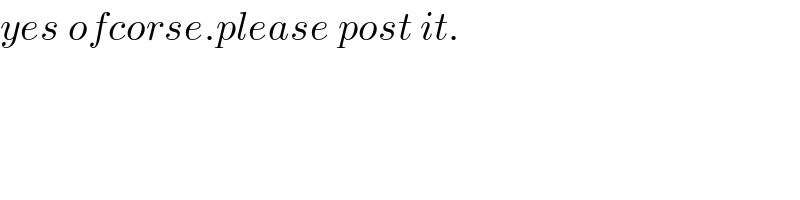
$${yes}\:{ofcorse}.{please}\:{post}\:{it}. \\ $$
Commented by Tinkutara last updated on 27/Jun/17

Commented by Tinkutara last updated on 27/Jun/17

$$\mathrm{This}\:\mathrm{is}\:\mathrm{my}\:\mathrm{book}'\mathrm{s}\:\mathrm{solution}.\:\mathrm{Please} \\ $$$$\mathrm{explain}\:\mathrm{the}\:\mathrm{last}\:\mathrm{line}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 27/Jun/17
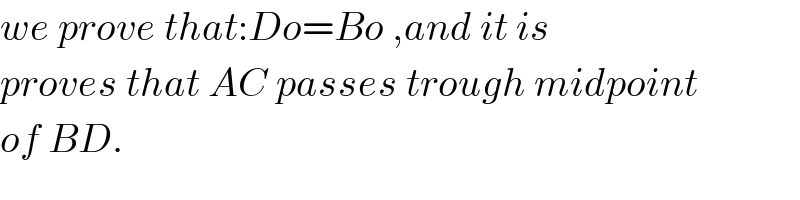
$${we}\:{prove}\:{that}:{Do}={Bo}\:,{and}\:{it}\:{is} \\ $$$${proves}\:{that}\:{AC}\:{passes}\:{trough}\:{midpoint} \\ $$$${of}\:{BD}. \\ $$
