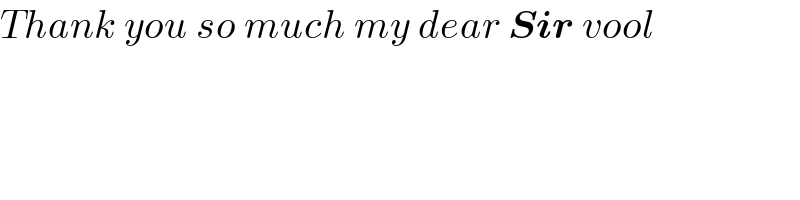Question Number 160658 by HongKing last updated on 04/Dec/21
![Find: lim_(x→0) 4x [ (1/(4x)) ] = ?](Q160658.png)
$$\boldsymbol{\mathrm{Find}}:\:\:\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{4}\boldsymbol{\mathrm{x}}\:\left[\:\frac{\mathrm{1}}{\mathrm{4}\boldsymbol{\mathrm{x}}}\:\right]\:=\:? \\ $$$$ \\ $$
Commented by mr W last updated on 04/Dec/21
![lim_(x→0) 4x[(1/(4x))] =lim_(t→∞) (([t])/t)=L t−1<[t]≤t lim_(t→∞) ((t−1)/t)<L≤lim_(t→∞) (t/t) 1<L≤1 ⇒L=1](Q160663.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}4}{x}\left[\frac{\mathrm{1}}{\mathrm{4}{x}}\right] \\ $$$$=\underset{{t}\rightarrow\infty} {\mathrm{lim}}\frac{\left[{t}\right]}{{t}}={L} \\ $$$${t}−\mathrm{1}<\left[{t}\right]\leqslant{t} \\ $$$$\underset{{t}\rightarrow\infty} {\mathrm{lim}}\frac{{t}−\mathrm{1}}{{t}}<{L}\leqslant\underset{{t}\rightarrow\infty} {\mathrm{lim}}\frac{{t}}{{t}} \\ $$$$\mathrm{1}<{L}\leqslant\mathrm{1} \\ $$$$\Rightarrow{L}=\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 04/Dec/21
$${very}\:{nice}\:{solution}\:{sir}\:{W} \\ $$
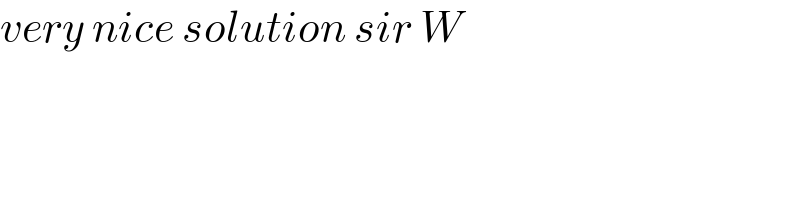
Commented by HongKing last updated on 04/Dec/21
$$\mathrm{Nice}\:\mathrm{solution}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{Sir}}\:\mathrm{thank}\:\mathrm{you} \\ $$
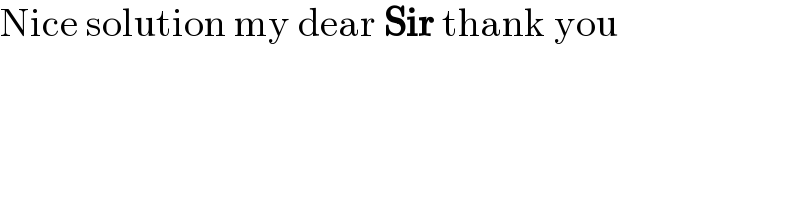
Answered by mathmax by abdo last updated on 04/Dec/21
![we have [(1/(4x))]≤(1/(4x))<[(1/(4x))]+1 ⇒(1/(4x))−1<[(1/(4x))]≤(1/(4x)) ⇒ for x>0 we have 1−4x<4x.[(1/(4x))]≤1 ⇒ lim_(x→0^+ ) 4x[(1/(4x))]=1](Q160686.png)
$$\mathrm{we}\:\mathrm{have}\:\left[\frac{\mathrm{1}}{\mathrm{4x}}\right]\leqslant\frac{\mathrm{1}}{\mathrm{4x}}<\left[\frac{\mathrm{1}}{\mathrm{4x}}\right]+\mathrm{1}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{4x}}−\mathrm{1}<\left[\frac{\mathrm{1}}{\mathrm{4x}}\right]\leqslant\frac{\mathrm{1}}{\mathrm{4x}}\:\Rightarrow \\ $$$$\mathrm{for}\:\mathrm{x}>\mathrm{0}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{1}−\mathrm{4x}<\mathrm{4x}.\left[\frac{\mathrm{1}}{\mathrm{4x}}\right]\leqslant\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\mathrm{4x}\left[\frac{\mathrm{1}}{\mathrm{4x}}\right]=\mathrm{1} \\ $$
Commented by HongKing last updated on 04/Dec/21
$${Thank}\:{you}\:{so}\:{much}\:{my}\:{dear}\:\boldsymbol{{Sir}}\:{vool} \\ $$