Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 160672 by LEKOUMA last updated on 04/Dec/21

$$Calculate$$$$\underset{x\to 0}{\lim }\frac{{tgx}^m}{{\left(\sin x\right)}^n},$$$$\underset{x\to 0}{\lim }\frac{x\cos x-x}{(e^x-1)\ln (1+3x^2)}$$

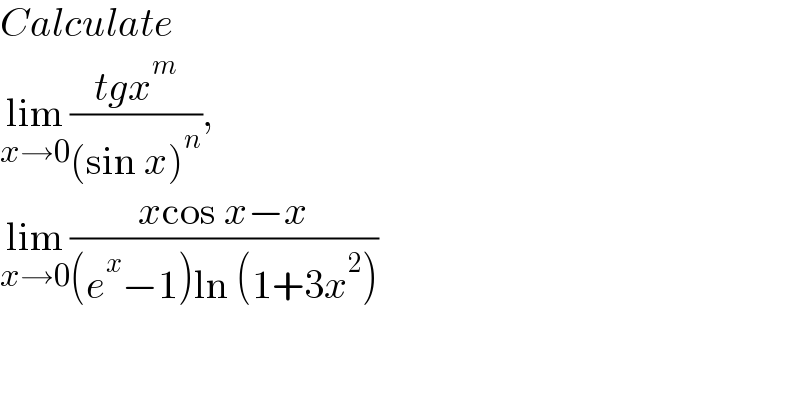
Commented by tounghoungko last updated on 04/Dec/21

$$\left(2\right)\underset{x\to 0}{\lim }\frac{\mathrm{x}\cos \mathrm{x}-\mathrm{x}}{({\mathrm{e}}^{\mathrm{x}}-1)\ln (1+{3\mathrm{x}}^2)}$$$$=\underset{x\to 0}{\lim }\frac{\mathrm{x}(\cos \mathrm{x}-1)}{({\mathrm{e}}^{\mathrm{x}}-1)\ln (1+{3\mathrm{x}}^2)}$$$$=\underset{x\to 0}{\lim }\frac{1}{\left(\frac{{\mathrm{e}}^{\mathrm{x}}-1}{\mathrm{x}}\right)}\times \underset{x\to 0}{\lim }\frac{-2\sin {}^2\left(\frac{1}{2}\mathrm{x}\right)}{\ln (1+{3\mathrm{x}}^2)}$$$$=1\times \underset{x\to 0}{\lim }\frac{-\frac{1}{2}{\mathrm{x}}^2}{\ln (1+{3\mathrm{x}}^2)}$$$$=-\frac{1}{2}\times \underset{x\to 0}{\lim }\frac{2\mathrm{x}}{\left(\frac{6\mathrm{x}}{(1+{3\mathrm{x}}^2)}\right)}$$$$=-\frac{1}{6}\times \underset{x\to 0}{\lim }(1+{3\mathrm{x}}^2)=-\frac{1}{6}$$

Answered by alephzero last updated on 04/Dec/21

$$1.\underset{x\to 0}{\lim }\frac{\mathrm{tg}\left(x^m\right)}{{\left(\sin x\right)}^n}=?$$$$n^0=1\iff n\in \mathbb{R}$$$$\mathrm{tg}0=0$$$$\mathrm{tg}1\approx 1.55741$$$$\Rightarrow \mathrm{tg}{0}^m=0\iff m>0$$$$\mathrm{tg}{0}^m\approx 1.55741\iff m=0$$$$\sin 0=0$$$$\Rightarrow {\left(\sin 0\right)}^n=0\iff n>0$$$${\left(\sin 0\right)}^n=1\iff n=0$$$$\Rightarrow \underset{x\to 0}{\lim }\frac{\mathrm{tg}{x}^m}{{\left(\sin x\right)}^n}=\pm \mathrm{\infty }\iff ((m>0)\wedge (n>0))$$$$\underset{x\to 0}{\lim }\frac{\mathrm{tg}{x}^m}{{\left(\sin x\right)}^n}=0\iff ((m>0)\wedge (n=0))$$$$\underset{x\to 0}{\lim }\frac{\mathrm{tg}{x}^m}{{\left(\sin x\right)}^n}\approx 1.55741\iff ((m=0)\wedge (n=0))$$$$Answeredbyalephzero,student$$$$of{6}^{th}grade.$$

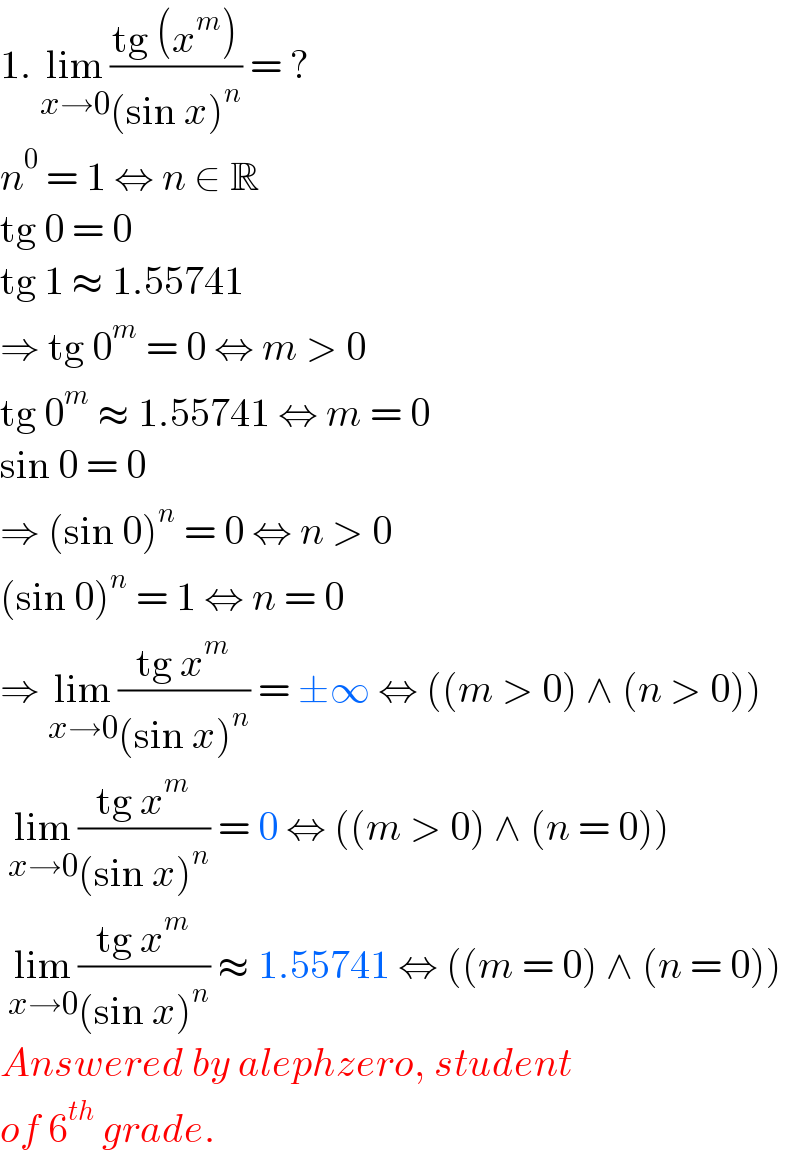
Commented by mr W last updated on 04/Dec/21

$$inthisforumallmembersareequal.$$$$one{doesn}^{\prime }tneedtotellifhe/sheis$$$$teacherorstudent,oldoryoung,man$$$$orwoman,IndianorJapanese,$$$$buddistormuslim,earthlingor$$$$marsian...onlyonethingis$$$$important:theylovemathematics.$$

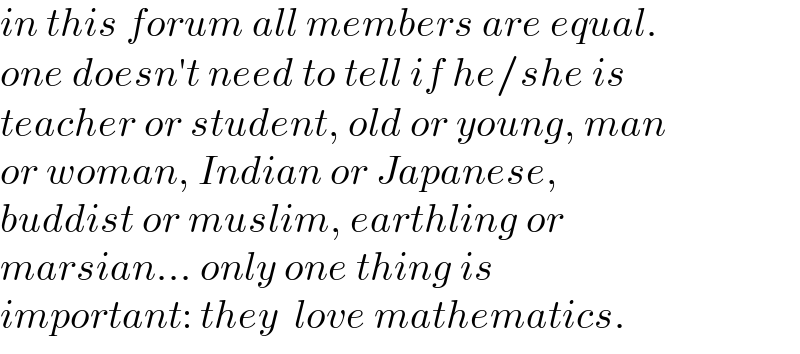
Commented by greg_ed last updated on 05/Dec/21

$$\mathrm{right}!$$

Answered by mr W last updated on 04/Dec/21

$$\left(1\right)$$$$=\underset{x\to 0}{\lim }\frac{\tan \left(x^m\right)}{x^m}\times {\left(\frac{x}{\sin x}\right)}^n\times x^{m-n}$$$$=\underset{x\to 0}{\lim }{x}^{m-n}=\{\begin{array}{l}1,ifm=n\\ 0,ifm>n\\ \mathrm{\infty },ifm<n\end{array}$$$$\left(2\right)$$$$=\underset{x\to 0}{\lim }\frac{x(-2{\sin }^2\frac{x}{2})}{(e^x-1)\ln (1+3x^2)}$$$$=\underset{x\to 0}{\lim }\frac{-2x{\sin }^2\frac{x}{2}}{(x+\frac{x^2}{2!}+...)(3x^2-\frac{9x^4}{2}+...)}$$$$=\underset{x\to 0}{\lim }\frac{-2{\sin }^2\frac{x}{2}}{(1+\frac{x}{2!}+...)(3-\frac{9x^2}{2}+...)x^2}$$$$=\underset{x\to 0}{\lim }\frac{-1}{(1+\frac{x}{2!}+...)(3-\frac{9x^2}{2}+...)\times 2}\times {\left(\frac{\sin \frac{x}{2}}{\frac{x}{2}}\right)}^2$$$$=-\frac{1}{1\times 3\times 2}\times 1^2$$$$=-\frac{1}{6}$$

Answered by Jamshidbek last updated on 05/Dec/21

$$\underset{x\to 0}{\lim }\frac{{\mathrm{tgx}}^{\mathrm{m}}}{{\left(\mathrm{sinx}\right)}^{\mathrm{n}}}=\underset{x\to 0}{\lim }\frac{{\mathrm{tgx}}^{\mathrm{m}}}{{\mathrm{x}}^{\mathrm{m}}}\cdot \frac{{\mathrm{x}}^{\mathrm{m}}}{{\left(\mathrm{sinx}\right)}^{\mathrm{n}}}=$$$$=\underset{x\to 0}{\lim }\frac{{\mathrm{x}}^{\mathrm{m}}\cdot {\mathrm{x}}^{\mathrm{m}}}{{\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)}^{\mathrm{n}}\cdot {\mathrm{x}}^{\mathrm{n}}}=\underset{x\to 0}{\lim }\frac{{\mathrm{x}}^{2\mathrm{m}}}{{\mathrm{x}}^{\mathrm{n}}}={\underset{x\to 0}{\lim x}}^{2\mathrm{m}-\mathrm{n}}=0$$

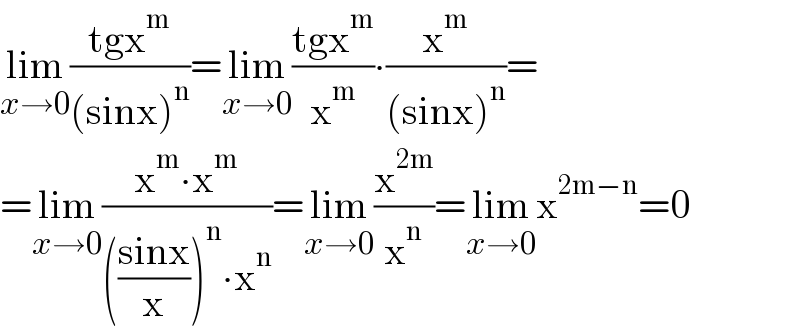
Commented by mr W last updated on 05/Dec/21

$$wrong!$$$$\lim \frac{{\mathrm{tgx}}^{\mathrm{m}}}{{\mathrm{x}}^{\mathrm{m}}}\cdot \frac{{\mathrm{x}}^{\mathrm{m}}}{{\left(\mathrm{sinx}\right)}^{\mathrm{n}}}\ne \lim \frac{{\mathrm{x}}^{\mathrm{m}}\cdot {\mathrm{x}}^{\mathrm{m}}}{{\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)}^{\mathrm{n}}\cdot {\mathrm{x}}^{\mathrm{n}}}$$$$x^{m}istoomuch.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com