Question Number 160706 by HongKing last updated on 05/Dec/21
Answered by mr W last updated on 05/Dec/21
![S_n =Σ_(k=1) ^n sin ((k/n^3 )) T_n =Σ_(k=1) ^n cos ((k/n^3 )) T_n +iS_n =Σ_(k=1) ^n {cos ((k/n^3 ))+i sin ((k/n^3 ))} T_n +iS_n =Σ_(k=1) ^n e^((ik)/n^3 ) =((e^(i/n^3 ) (e^((in)/n^3 ) −1))/(e^(i/n^3 ) −1)) T_n +iS_n =(((cos (1/n^3 )+i sin (1/n^3 ))[(cos (1/n^2 )−1)+i sin (1/n^2 )])/((cos (1/n^3 )−1)+isin (1/n^3 ))) T_n +iS_n =(([cos (1/n^3 ) (cos (1/n^2 )−1)−sin (1/n^3 ) sin (1/n^2 )]+i[cos (1/n^3 ) sin (1/n^2 )+sin (1/n^3 ) (cos (1/n^2 )−1)])/((cos (1/n^3 )−1)+isin (1/n^3 ))) T_n +iS_n =(([cos ((1/n^3 )+(1/n^2 ))−cos (1/n^3 )]+i[ sin ((1/n^3 )+(1/n^2 ))−sin (1/n^3 ) ])/((cos (1/n^3 )−1)+isin (1/n^3 ))) T_n +iS_n =(({[cos ((1/n^3 )+(1/n^2 ))−cos (1/n^3 )]+i[ sin ((1/n^3 )+(1/n^2 ))−sin (1/n^3 ) ]}[(cos (1/n^3 )−1)−isin (1/n^3 )])/((cos (1/n^3 )−1)^2 +(sin (1/n^3 ))^2 )) T_n +iS_n =(({(cos ((n+1)/n^3 )−cos (1/n^3 ))(cos (1/n^3 )−1)+sin (1/n^3 ) ( sin ((n+1)/n^3 )−sin (1/n^3 ))}+i{(cos (1/n^3 )−1)( sin ((n+1)/n^3 )−sin (1/n^3 ))−sin (1/n^3 ) (cos ((n+1)/n^3 )−cos (1/n^3 ))})/((cos (1/n^3 )−1)^2 +(sin (1/n^3 ))^2 )) ⇒T_n =(((cos ((n+1)/n^3 )−cos (1/n^3 ))(cos (1/n^3 )−1)+sin (1/n^3 ) ( sin ((n+1)/n^3 )−sin (1/n^3 )))/((cos (1/n^3 )−1)^2 +(sin (1/n^3 ))^2 )) ⇒T_n =(1/2){((cos (1/n^2 )−cos ((1/n^3 )+(1/n^2 ))cos (1/n^3 ))/(1−cos (1/n^3 )))−1} ⇒T_n =(1/2){((sin (1/n^3 ) sin ((1/n^3 )+ (1/n^2 )))/(1−cos (1/n^3 )))−1} ⇒S_n =(((cos (1/n^3 )−1)( sin ((n+1)/n^3 )−sin (1/n^3 ))−sin (1/n^3 ) (cos ((n+1)/n^3 )−cos (1/n^3 )))/((cos (1/n^3 )−1)^2 +(sin (1/n^3 ))^2 )) ⇒S_n =((sin (1/n^3 )+sin (1/n^2 )−sin ((1/n^3 )+(1/n^2 )))/(2(1−cos (1/n^3 )))) ⇒S_n =(1/2){((1−cos (1/n^2 ))/(1−cos (1/n^3 )))×sin (1/n^3 )+sin (1/n^2 )} lim_(n→∞) S_n =(1/2)lim_(n→∞) {((1−cos (1/n^2 ))/(1−cos (1/n^3 )))×sin (1/n^3 )+sin (1/n^2 )} =(1/2)lim_(x→0) {((1−cos x^2 )/(1−cos x^3 ))×sin x^3 +sin x^2 } =(1/2)lim_(x→0) {0+0} =0 lim_(x→0) {((1−cos x^2 )/(1−cos x^3 ))×sin x^3 } =lim_(x→0) {(((x^4 /2)−(x^8 /(24))+...)/((x^6 /2)−(x^(12) /(24))+...))×(x^3 −(x^6 /6)+...)} =lim_(x→0) {((x((1/2)−(x^4 /(24))+...))/((1/2)−(x^6 /(24))+...))×(1−(x^3 /6)+...)} =0](Q160715.png)
$${S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{sin}\:\left(\frac{{k}}{{n}^{\mathrm{3}} }\right) \\ $$$${T}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{cos}\:\left(\frac{{k}}{{n}^{\mathrm{3}} }\right) \\ $$$${T}_{{n}} +{iS}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left\{\mathrm{cos}\:\left(\frac{{k}}{{n}^{\mathrm{3}} }\right)+{i}\:\mathrm{sin}\:\left(\frac{{k}}{{n}^{\mathrm{3}} }\right)\right\} \\ $$$${T}_{{n}} +{iS}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{\frac{{ik}}{{n}^{\mathrm{3}} }} =\frac{{e}^{\frac{{i}}{{n}^{\mathrm{3}} }} \left({e}^{\frac{{in}}{{n}^{\mathrm{3}} }} −\mathrm{1}\right)}{{e}^{\frac{{i}}{{n}^{\mathrm{3}} }} −\mathrm{1}} \\ $$$${T}_{{n}} +{iS}_{{n}} =\frac{\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }+{i}\:\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)\left[\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{1}\right)+{i}\:\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right]}{\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{1}\right)+{i}\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }} \\ $$$${T}_{{n}} +{iS}_{{n}} =\frac{\left[\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{1}\right)−\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right]+{i}\left[\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{1}\right)\right]}{\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{1}\right)+{i}\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }} \\ $$$${T}_{{n}} +{iS}_{{n}} =\frac{\left[\mathrm{cos}\:\left(\frac{\mathrm{1}}{{n}^{\mathrm{3}} }+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right]+{i}\left[\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{{n}^{\mathrm{3}} }+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)−\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\right]}{\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{1}\right)+{i}\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }} \\ $$$${T}_{{n}} +{iS}_{{n}} =\frac{\left\{\left[\mathrm{cos}\:\left(\frac{\mathrm{1}}{{n}^{\mathrm{3}} }+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right]+{i}\left[\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{{n}^{\mathrm{3}} }+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)−\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\right]\right\}\left[\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{1}\right)−{i}\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right]}{\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)^{\mathrm{2}} } \\ $$$${T}_{{n}} +{iS}_{{n}} =\frac{\left\{\left(\mathrm{cos}\:\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{1}\right)+\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\left(\:\mathrm{sin}\:\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)\right\}+{i}\left\{\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{1}\right)\left(\:\mathrm{sin}\:\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)−\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\left(\mathrm{cos}\:\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)\right\}}{\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{T}_{{n}} =\frac{\left(\mathrm{cos}\:\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{1}\right)+\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\left(\:\mathrm{sin}\:\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)}{\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{T}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{cos}\:\left(\frac{\mathrm{1}}{{n}^{\mathrm{3}} }+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }}{\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }}−\mathrm{1}\right\} \\ $$$$\Rightarrow{T}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{{n}^{\mathrm{3}} }+\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)}{\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }}−\mathrm{1}\right\} \\ $$$$\Rightarrow{S}_{{n}} =\frac{\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{1}\right)\left(\:\mathrm{sin}\:\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)−\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\left(\mathrm{cos}\:\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)}{\left(\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{S}_{{n}} =\frac{\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }+\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{sin}\:\left(\frac{\mathrm{1}}{{n}^{\mathrm{3}} }+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)} \\ $$$$\Rightarrow{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }}{\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }}×\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }+\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right\} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\frac{\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }}{\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }}×\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }+\mathrm{sin}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\mathrm{1}−\mathrm{cos}\:{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{cos}\:{x}^{\mathrm{3}} }×\mathrm{sin}\:{x}^{\mathrm{3}} +\mathrm{sin}\:{x}^{\mathrm{2}} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\mathrm{0}+\mathrm{0}\right\} \\ $$$$=\mathrm{0} \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\mathrm{1}−\mathrm{cos}\:{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{cos}\:{x}^{\mathrm{3}} }×\mathrm{sin}\:{x}^{\mathrm{3}} \right\} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\frac{{x}^{\mathrm{4}} }{\mathrm{2}}−\frac{{x}^{\mathrm{8}} }{\mathrm{24}}+...}{\frac{{x}^{\mathrm{6}} }{\mathrm{2}}−\frac{{x}^{\mathrm{12}} }{\mathrm{24}}+...}×\left({x}^{\mathrm{3}} −\frac{{x}^{\mathrm{6}} }{\mathrm{6}}+...\right)\right\} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{{x}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}^{\mathrm{4}} }{\mathrm{24}}+...\right)}{\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}^{\mathrm{6}} }{\mathrm{24}}+...}×\left(\mathrm{1}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+...\right)\right\} \\ $$$$=\mathrm{0} \\ $$
Answered by mindispower last updated on 05/Dec/21
![0≤sin(x)≤x,∀x∈[0,(π/2)] proof ,cos(x)≤1⇒∫_0 ^t cos(x)dx≤∫_0 ^t dx ⇔sin(t)≤t ∀k∈[1,n],(k/n^3 )∈[0,1[⊂[0,(π/2)] 0≤S_n ≤Σ_(k=1) ^n (k/n^3 )=(1/n^3 ).((n(1+n))/2) ⇒LimS_n =0](Q160724.png)
$$\mathrm{0}\leqslant{sin}\left({x}\right)\leqslant{x},\forall{x}\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right] \\ $$$${proof}\:,{cos}\left({x}\right)\leqslant\mathrm{1}\Rightarrow\int_{\mathrm{0}} ^{{t}} {cos}\left({x}\right){dx}\leqslant\int_{\mathrm{0}} ^{{t}} {dx} \\ $$$$\Leftrightarrow{sin}\left({t}\right)\leqslant{t} \\ $$$$\forall{k}\in\left[\mathrm{1},{n}\right],\frac{{k}}{{n}^{\mathrm{3}} }\in\left[\mathrm{0},\mathrm{1}\left[\subset\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right]\right.\right. \\ $$$$\mathrm{0}\leqslant{S}_{{n}} \leqslant\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}}{{n}^{\mathrm{3}} }=\frac{\mathrm{1}}{{n}^{\mathrm{3}} }.\frac{{n}\left(\mathrm{1}+{n}\right)}{\mathrm{2}} \\ $$$$\Rightarrow{LimS}_{{n}} =\mathrm{0} \\ $$$$ \\ $$
Commented by mr W last updated on 05/Dec/21
$${nice}\:{method}\:{for}\:{the}\:{limit}! \\ $$$${can}\:{you}\:{please}\:{comfirm}\:{if}\:{my} \\ $$$${formulas}\:{for}\:{S}_{{n}} \:{and}\:{T}_{{n}} \:{are}\:{correct}? \\ $$
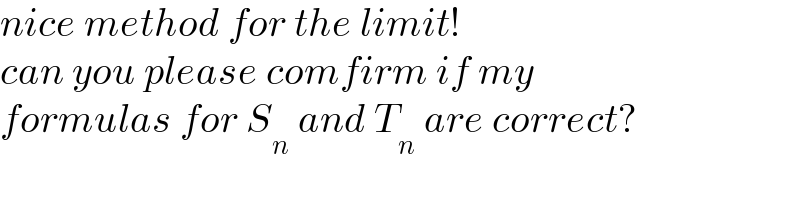
Commented by mindispower last updated on 05/Dec/21
$${thank}\:{You} \\ $$$${nice}\:{way}\:{you}\:{go}\:{thro}\:{too} \\ $$$${correct}\:{way}\:{sir}\:\:{nice}\:{day} \\ $$
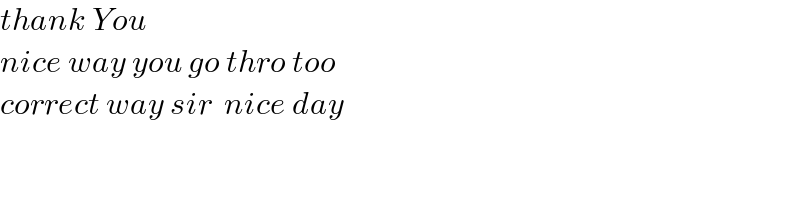
Commented by mr W last updated on 06/Dec/21
$${thanks}\:{sir}! \\ $$
Answered by qaz last updated on 05/Dec/21
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{sin}\:\left(\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{3}} }\right)=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{3}} }+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\right)\right)=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)\right)=\mathrm{0} \\ $$
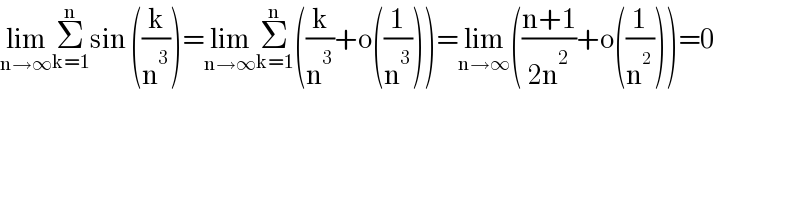
Answered by mathmax by abdo last updated on 06/Dec/21
$$\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \mathrm{sin}\left(\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{3}} }\right)\:\:\mathrm{we}\:\mathrm{know}\:\:\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\leqslant\mathrm{sinx}\leqslant\mathrm{x}\:\Rightarrow \\ $$$$\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{6}}\frac{\mathrm{k}^{\mathrm{3}} }{\mathrm{n}^{\mathrm{9}} }\leqslant\mathrm{sin}\left(\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{3}} }\right)\leqslant\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{3}} }\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}−\frac{\mathrm{1}}{\mathrm{6n}^{\mathrm{9}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{3}} \:\leqslant\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \mathrm{sin}\left(\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{3}} }\right)\leqslant\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}\:\Rightarrow \\ $$$$\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2n}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{6n}^{\mathrm{9}} }\frac{\mathrm{n}^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\leqslant\mathrm{S}_{\mathrm{n}} \leqslant\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2n}^{\mathrm{3}} }\:\Rightarrow \\ $$$$\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }−\frac{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{24n}^{\mathrm{7}} }\left(\rightarrow\mathrm{0}\right)\leqslant\mathrm{S}_{\mathrm{n}} \leqslant\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }\left(\rightarrow\mathrm{0}\right)\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{S}_{\mathrm{n}} =\mathrm{0} \\ $$$$ \\ $$