Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 16072 by Tinkutara last updated on 17/Jun/17

Let ABCD be a convex quadrilateral. Prove that the orthocenters of the triangles ABC, BCD, CDA and DAB are the vertices of a quadrilateral congruent to ABCD and prove that the centroids of the same triangles are the vertices of a cyclic quadrilateral.

$$\mathrm{Let}\:{ABCD}\:\mathrm{be}\:\mathrm{a}\:\mathrm{convex}\:\mathrm{quadrilateral}. \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{orthocenters}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{triangles}\:{ABC},\:{BCD},\:{CDA}\:\mathrm{and}\:{DAB} \\ $$$$\mathrm{are}\:\mathrm{the}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{a}\:\mathrm{quadrilateral} \\ $$$$\mathrm{congruent}\:\mathrm{to}\:{ABCD}\:\mathrm{and}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{the} \\ $$$$\mathrm{centroids}\:\mathrm{of}\:\mathrm{the}\:\mathrm{same}\:\mathrm{triangles}\:\mathrm{are}\:\mathrm{the} \\ $$$$\mathrm{vertices}\:\mathrm{of}\:\mathrm{a}\:\mathrm{cyclic}\:\mathrm{quadrilateral}. \\ $$

Commented by mrW1 last updated on 06/Jul/17

the question seems to be wrong. I think the centroids are the vertices of a quadrilateral congruent to ABCD. For part 1 please post a figure to show what is meant.

$$\mathrm{the}\:\mathrm{question}\:\mathrm{seems}\:\mathrm{to}\:\mathrm{be}\:\mathrm{wrong}.\:\mathrm{I}\:\mathrm{think} \\ $$$$\mathrm{the}\:\mathrm{centroids}\:\mathrm{are}\:\mathrm{the}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{a} \\ $$$$\mathrm{quadrilateral}\:\mathrm{congruent}\:\mathrm{to}\:\mathrm{ABCD}. \\ $$$$ \\ $$$$\mathrm{For}\:\mathrm{part}\:\mathrm{1}\:\mathrm{please}\:\mathrm{post}\:\mathrm{a}\:\mathrm{figure}\:\mathrm{to} \\ $$$$\mathrm{show}\:\mathrm{what}\:\mathrm{is}\:\mathrm{meant}. \\ $$

Commented by mrW1 last updated on 06/Jul/17

yes please.

$$\mathrm{yes}\:\mathrm{please}. \\ $$

Commented by mrW1 last updated on 06/Jul/17

I can prove that the centroids are the vertices of a quadrilateral congruent to ABCD. Its area is (1/9) of the area of ABCD.

$$\mathrm{I}\:\mathrm{can}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{centroids}\:\mathrm{are}\:\mathrm{the}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{a} \\ $$$$\mathrm{quadrilateral}\:\mathrm{congruent}\:\mathrm{to}\:\mathrm{ABCD}.\:\mathrm{Its} \\ $$$$\mathrm{area}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{9}}\:\mathrm{of}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{ABCD}. \\ $$

Answered by Tinkutara last updated on 07/Jul/17

Commented by Tinkutara last updated on 07/Jul/17

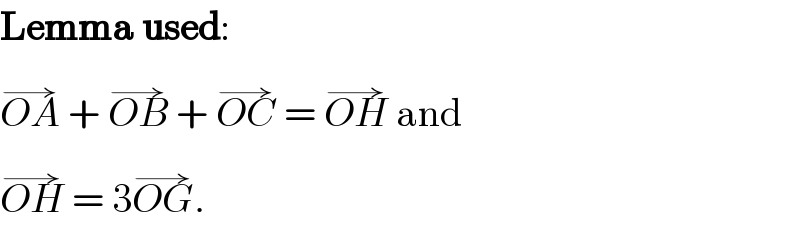
Lemma used: OA^(→) + OB^(→) + OC^(→) = OH^(→) and OH^(→) = 3OG^(→) .

$$\boldsymbol{\mathrm{Lemma}}\:\boldsymbol{\mathrm{used}}: \\ $$$$\overset{\rightarrow} {{OA}}\:+\:\overset{\rightarrow} {{OB}}\:+\:\overset{\rightarrow} {{OC}}\:=\:\overset{\rightarrow} {{OH}}\:\mathrm{and} \\ $$$$\overset{\rightarrow} {{OH}}\:=\:\mathrm{3}\overset{\rightarrow} {{OG}}. \\ $$

Commented by Tinkutara last updated on 07/Jul/17

Proof: Let O be circumcenter of the quadrilateral ABCD and let H_A , H_B , H_C , H_D be the orthocenters of the triangles BCD, CDA, DAB and ABC, respectively. Using the lemma, we have H_A H_B ^(→) = OH_B ^(→) − OH_A ^(→) = (OC^(→) + OB^(→) + OA^(→) ) − (OB^(→) + OC^(→) + OD^(→) ) = OA^(→) − OB^(→) = BA^(→) , and consequently the segments H_A H_B and AB are parallel and equal in length. We conclude that the quadrilaterals ABCD and H_A H_B H_C H_D are congruent. For the second claim, let G_A , G_B , G_C and G_D denote the centroids. It follows from the observation above that G_A G_B G_C G_D is obtained from H_A H_B H_C H_D by a homothetic of center O and ratio (1/3). Because H_A H_B H_C H_D is cyclic, the same is true of G_A G_B G_C G_D . (See Figure 5.27).

$$\boldsymbol{\mathrm{Proof}}: \\ $$$$\mathrm{Let}\:{O}\:\mathrm{be}\:\mathrm{circumcenter}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{quadrilateral}\:{ABCD}\:\mathrm{and}\:\mathrm{let}\:{H}_{{A}} ,\:{H}_{{B}} , \\ $$$${H}_{{C}} ,\:{H}_{{D}} \:\mathrm{be}\:\mathrm{the}\:\mathrm{orthocenters}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{triangles}\:{BCD},\:{CDA},\:{DAB}\:\mathrm{and} \\ $$$${ABC},\:\mathrm{respectively}.\:\mathrm{Using}\:\mathrm{the}\:\mathrm{lemma}, \\ $$$$\mathrm{we}\:\mathrm{have} \\ $$$$\overset{\rightarrow} {{H}_{{A}} {H}_{{B}} }\:=\:\overset{\rightarrow} {{OH}_{{B}} }\:−\:\overset{\rightarrow} {{OH}_{{A}} } \\ $$$$=\:\left(\overset{\rightarrow} {{OC}}\:+\:\overset{\rightarrow} {{OB}}\:+\:\overset{\rightarrow} {{OA}}\right)\:−\:\left(\overset{\rightarrow} {{OB}}\:+\:\overset{\rightarrow} {{OC}}\:+\:\overset{\rightarrow} {{OD}}\right) \\ $$$$=\:\overset{\rightarrow} {{OA}}\:−\:\overset{\rightarrow} {{OB}}\:=\:\overset{\rightarrow} {{BA}}, \\ $$$$\mathrm{and}\:\mathrm{consequently}\:\mathrm{the}\:\mathrm{segments}\:{H}_{{A}} {H}_{{B}} \\ $$$$\mathrm{and}\:{AB}\:\mathrm{are}\:\mathrm{parallel}\:\mathrm{and}\:\mathrm{equal}\:\mathrm{in} \\ $$$$\mathrm{length}.\:\mathrm{We}\:\mathrm{conclude}\:\mathrm{that}\:\mathrm{the} \\ $$$$\mathrm{quadrilaterals}\:{ABCD}\:\mathrm{and}\:{H}_{{A}} {H}_{{B}} {H}_{{C}} {H}_{{D}} \\ $$$$\mathrm{are}\:\mathrm{congruent}. \\ $$$$\mathrm{For}\:\mathrm{the}\:\mathrm{second}\:\mathrm{claim},\:\mathrm{let}\:{G}_{{A}} ,\:{G}_{{B}} ,\:{G}_{{C}} \\ $$$$\mathrm{and}\:{G}_{{D}} \:\mathrm{denote}\:\mathrm{the}\:\mathrm{centroids}.\:\mathrm{It}\:\mathrm{follows} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{observation}\:\mathrm{above}\:\mathrm{that} \\ $$$${G}_{{A}} {G}_{{B}} {G}_{{C}} {G}_{{D}} \:\mathrm{is}\:\mathrm{obtained}\:\mathrm{from} \\ $$$${H}_{{A}} {H}_{{B}} {H}_{{C}} {H}_{{D}} \:\mathrm{by}\:\mathrm{a}\:\mathrm{homothetic}\:\mathrm{of}\:\mathrm{center} \\ $$$${O}\:\mathrm{and}\:\mathrm{ratio}\:\frac{\mathrm{1}}{\mathrm{3}}.\:\mathrm{Because}\:{H}_{{A}} {H}_{{B}} {H}_{{C}} {H}_{{D}} \\ $$$$\mathrm{is}\:\mathrm{cyclic},\:\mathrm{the}\:\mathrm{same}\:\mathrm{is}\:\mathrm{true}\:\mathrm{of}\:{G}_{{A}} {G}_{{B}} {G}_{{C}} {G}_{{D}} . \\ $$$$\left(\mathrm{See}\:\mathrm{Figure}\:\mathrm{5}.\mathrm{27}\right). \\ $$

Commented by Tinkutara last updated on 07/Jul/17

Commented by mrW1 last updated on 07/Jul/17

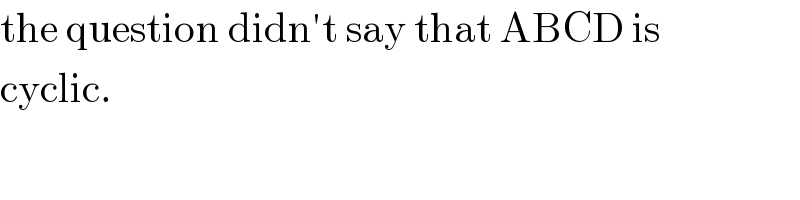
the question didn′t say that ABCD is cyclic.

$$\mathrm{the}\:\mathrm{question}\:\mathrm{didn}'\mathrm{t}\:\mathrm{say}\:\mathrm{that}\:\mathrm{ABCD}\:\mathrm{is} \\ $$$$\mathrm{cyclic}. \\ $$

Commented by mrW1 last updated on 07/Jul/17

the answer given doesn′t match the question. i can not understand.

$$\mathrm{the}\:\mathrm{answer}\:\mathrm{given}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{match}\:\mathrm{the} \\ $$$$\mathrm{question}.\:\mathrm{i}\:\mathrm{can}\:\mathrm{not}\:\mathrm{understand}. \\ $$

Commented by mrW1 last updated on 07/Jul/17

i have said the question is not correct. so i can not give a solution to it. the proof i meant is following. but it is not the proof to your question exactly.

$$\mathrm{i}\:\mathrm{have}\:\mathrm{said}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct}. \\ $$$$\mathrm{so}\:\mathrm{i}\:\mathrm{can}\:\mathrm{not}\:\mathrm{give}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{it}.\: \\ $$$$\mathrm{the}\:\mathrm{proof}\:\mathrm{i}\:\mathrm{meant}\:\mathrm{is}\:\mathrm{following}.\:\mathrm{but}\:\mathrm{it} \\ $$$$\mathrm{is}\:\mathrm{not}\:\mathrm{the}\:\mathrm{proof}\:\mathrm{to}\:\mathrm{your}\:\mathrm{question}\:\mathrm{exactly}. \\ $$

Commented by mrW1 last updated on 07/Jul/17

Commented by mrW1 last updated on 07/Jul/17

ABCD is an any convex quadrilateral. K,L,M,N are the centroids described. ((GM)/(GB))=(1/3) ((GN)/(GC))=(1/3) ⇒MN//BC and MN=((BC)/3) similarly NL//AB and NL=((AB)/3) LK//AD and LK=((AD)/3) KM//DC and KM=((DC)/3) ⇒LKNM is congruent to ABCD ⇒Area [KLNM]=(1/9) Area [ABCD]

$$\mathrm{ABCD}\:\mathrm{is}\:\mathrm{an}\:\mathrm{any}\:\mathrm{convex}\:\mathrm{quadrilateral}. \\ $$$$\mathrm{K},\mathrm{L},\mathrm{M},\mathrm{N}\:\mathrm{are}\:\mathrm{the}\:\mathrm{centroids}\:\mathrm{described}. \\ $$$$\frac{\mathrm{GM}}{\mathrm{GB}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\frac{\mathrm{GN}}{\mathrm{GC}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{MN}//\mathrm{BC}\:\mathrm{and}\:\mathrm{MN}=\frac{\mathrm{BC}}{\mathrm{3}} \\ $$$$\mathrm{similarly} \\ $$$$\mathrm{NL}//\mathrm{AB}\:\mathrm{and}\:\mathrm{NL}=\frac{\mathrm{AB}}{\mathrm{3}} \\ $$$$\mathrm{LK}//\mathrm{AD}\:\mathrm{and}\:\mathrm{LK}=\frac{\mathrm{AD}}{\mathrm{3}} \\ $$$$\mathrm{KM}//\mathrm{DC}\:\mathrm{and}\:\mathrm{KM}=\frac{\mathrm{DC}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{LKNM}\:\mathrm{is}\:\mathrm{congruent}\:\mathrm{to}\:\mathrm{ABCD} \\ $$$$\Rightarrow\mathrm{Area}\:\left[\mathrm{KLNM}\right]=\frac{\mathrm{1}}{\mathrm{9}}\:\mathrm{Area}\:\left[\mathrm{ABCD}\right] \\ $$

Commented by mrW1 last updated on 07/Jul/17

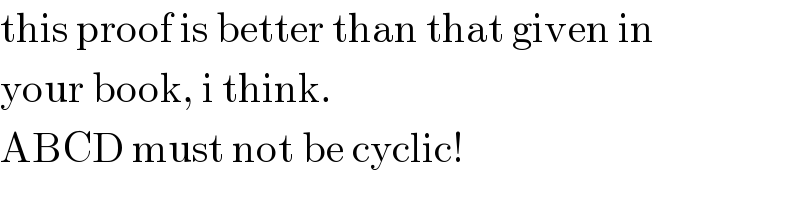
this proof is better than that given in your book, i think. ABCD must not be cyclic!

$$\mathrm{this}\:\mathrm{proof}\:\mathrm{is}\:\mathrm{better}\:\mathrm{than}\:\mathrm{that}\:\mathrm{given}\:\mathrm{in} \\ $$$$\mathrm{your}\:\mathrm{book},\:\mathrm{i}\:\mathrm{think}. \\ $$$$\mathrm{ABCD}\:\mathrm{must}\:\mathrm{not}\:\mathrm{be}\:\mathrm{cyclic}! \\ $$

Commented by Tinkutara last updated on 08/Jul/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com