Find the limit of this sequence. (√2),(√(2(√2))),(√(2(√(2(√2))))),(√(2(√(2(√(2(√2))))))),... Show that the sum of the terms of this infinite sequence does not converge.


Question and Answers Forum

All Questions Topic List
Limits Questions
Previous in All Question Next in All Question
Previous in Limits Next in Limits
Question Number 1608 by 112358 last updated on 26/Aug/15

$F i n d t h e l i m i t o f t h i s s e q u e n c e .$ $\sqrt{2}, \sqrt{2 \sqrt{2}}, \sqrt{2 \sqrt{2 \sqrt{2}}}, \sqrt{2 \sqrt{2 \sqrt{2 \sqrt{2}}}}, . . .$ $S h o w t h a t t h e s u m o f t h e$ $t e r m s o f t h i s i n f i n i t e s e q u e n c e$ $d o e s n o t c o n v e r g e .$
Commented by Rasheed Ahmad last updated on 26/Aug/15

$L e t \sqrt{2 \sqrt{2 \sqrt{2 \sqrt{2 . . .}}}} = x$ $S q u a r i n g b o t h s i d e s,$ $2 \sqrt{2 \sqrt{2 \sqrt{2 . . .}}} = x^{2}$ $2 . x = x^{2}$ $x = 2$ $T h e l i m i t o f t h e s e q u e n c e = 2$
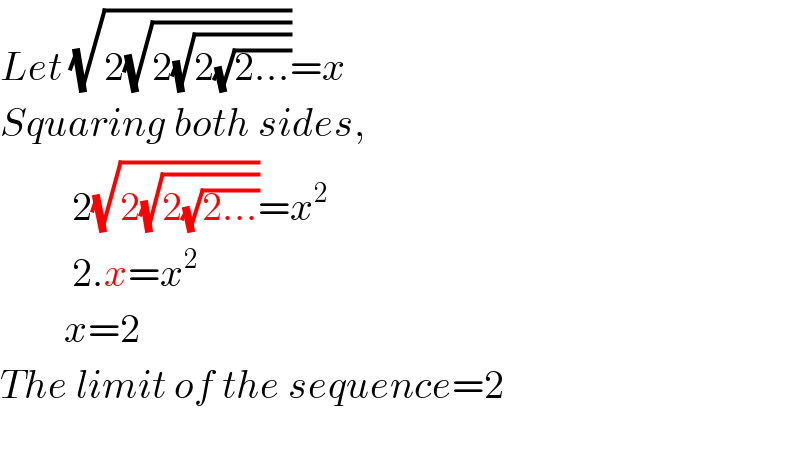
Commented by 112358 last updated on 26/Aug/15

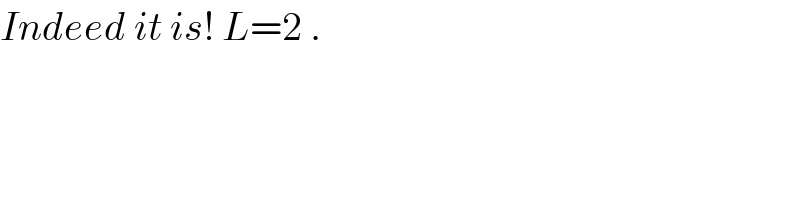
$I n d e e d i t i s! L = 2 .$
	Answered by 123456 last updated on 26/Aug/15

	$a_{n} = \sqrt{2 a_{n - 1}}$ $a_{0} = \sqrt{2}$ $a_{n} > 0 \Rightarrow 2 a_{n} > 0 \Rightarrow \sqrt{2 a_{n}} > 0 \Rightarrow a_{n + 1} > 0$ $0 < a_{n} < 2 \Rightarrow 0 < 2 a_{n} < 4 \Rightarrow 0 < \sqrt{2 a_{n}} < 2 \Rightarrow 0 < a_{n + 1} < 2$ $0 < a_{n} < a_{n + 1} < 2 \Rightarrow 0 < 2 a_{n} < 2 a_{n + 1} < 4 \Rightarrow 0 < \sqrt{2 a_{n}} < \sqrt{2 a_{n + 1}} < 2 \Rightarrow 0 < a_{n + 1} < a_{n + 2} < 2$ $0 < a_{n + 1} < a_{n} < 2 \Rightarrow 0 < 2 a_{n + 1} < 2 a_{n} < 4 \Rightarrow 0 < \sqrt{2 a_{n + 1}} < \sqrt{2 a_{n}} < 2 \Rightarrow 0 < a_{n + 2} < a_{n + 1} < 2$ $a_{0} = \sqrt{2}, a_{1} = \sqrt{2 \sqrt{2}} \Rightarrow a_{1} > a_{0}, the a is crescent$ $since a is bounced and crescent, \lim_{n \to + \infty} a_{n} exists$ $a_{n + 1} = a_{n} = a$ $a = \sqrt{2 a} \Rightarrow a^{2} = 2 a \Rightarrow a (a - 2) = 0 \Rightarrow a = 0 \lor a = 2$ $since it crescent them a = 2, \lim_{n \to + \infty} a_{n} = a = 2$ $S = \underset{n = 0}{\sum^{+ \infty}} a_{n}$ $since \lim_{n \to + \infty} a_{n} \neq 0, then the serie diverge$
	Commented by Rasheed Ahmad last updated on 27/Aug/15

	$W h a t i s m e a n t b y^{'} {c r e s c e n t}^{'} ?$ $I a m a s k i n g f o r t h e s a k e o f$ $k n o w l e d g e .$
	Commented by 123456 last updated on 27/Aug/15

	$growing or something like this (sorry about my bad english)$ $as shown$ $0 < a_{n} < a_{n + 1} < 2 \Rightarrow 0 < a_{n + 1} < a_{n + 2} < 2$ $since 0 < a_{0} < a_{1} < 2, them (0 < 2 < 2 \sqrt{2} < 4 \Rightarrow 0 < \sqrt{2} < \sqrt{2 \sqrt{2}} < 2)$ $0 < a_{0} < a_{1} < a_{2} < a_{3} < \cdot \cdot \cdot < 2$
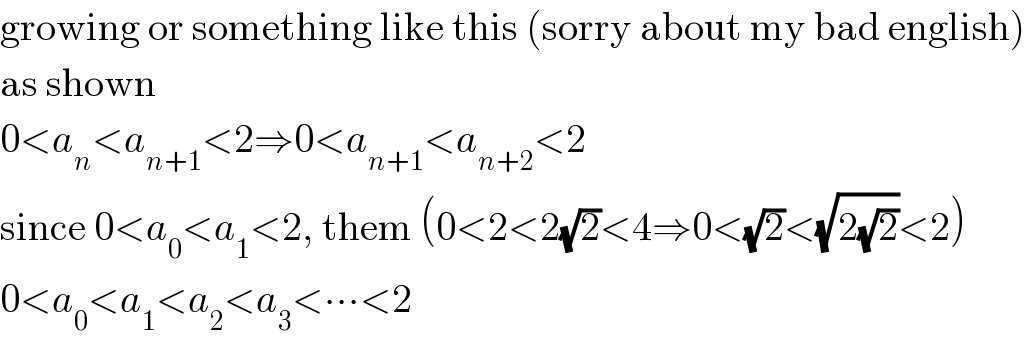
	Commented by 112358 last updated on 27/Aug/15

	$H e / {s h e}^{'} s s a y i n g t h a t t h e t e r m s$ $o f t h e s e q u e n c e a r e p e r p e t u a l l y$ $i n c r e a s i n g t o a l i m i t i n g v a l u e o f$ $2 . H e n c e, t h e s e q u e n c e i s$ $m o n o t o n i c a n d u p p e r b o u n d e d .$ $i . e a_{n} ⩽ M f o r a l l n a n d$ $a_{n + 1} ⩾ a_{n} f o r a l l n .$ $G e n e r a l l y, a l l s e q u e n c e s w h i c h$ $a r e m o n o t o n i c (o n l y i n c r e a s i n g$ $o r d e c r e a s i n g b u t n o t b o t h) a n d b o u n d e d$ $(u p p e r o r l o w e r [a_{n} > M f o r a n y$ $f i n i t e n]) a r e c o n v e r g e n t . T h i s$ $i s c a l l e d t h e m o n o t o n i c$ $s e q u e n c e t h e o r e m .$
	Commented by Rasheed Ahmad last updated on 27/Aug/15

	$Thanks to both of you!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum