Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 160922 by KONE last updated on 09/Dec/21

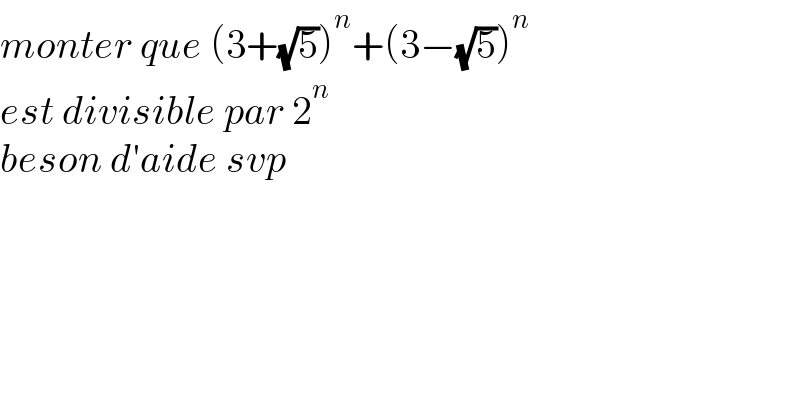
monter que (3+(√5))^n +(3−(√5))^(n ) est divisible par 2^n beson d′aide svp

$${monter}\:{que}\:\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)^{{n}} +\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)^{{n}\:} \\ $$$${est}\:{divisible}\:{par}\:\mathrm{2}^{{n}} \\ $$$${beson}\:{d}'{aide}\:{svp} \\ $$

Answered by mindispower last updated on 09/Dec/21

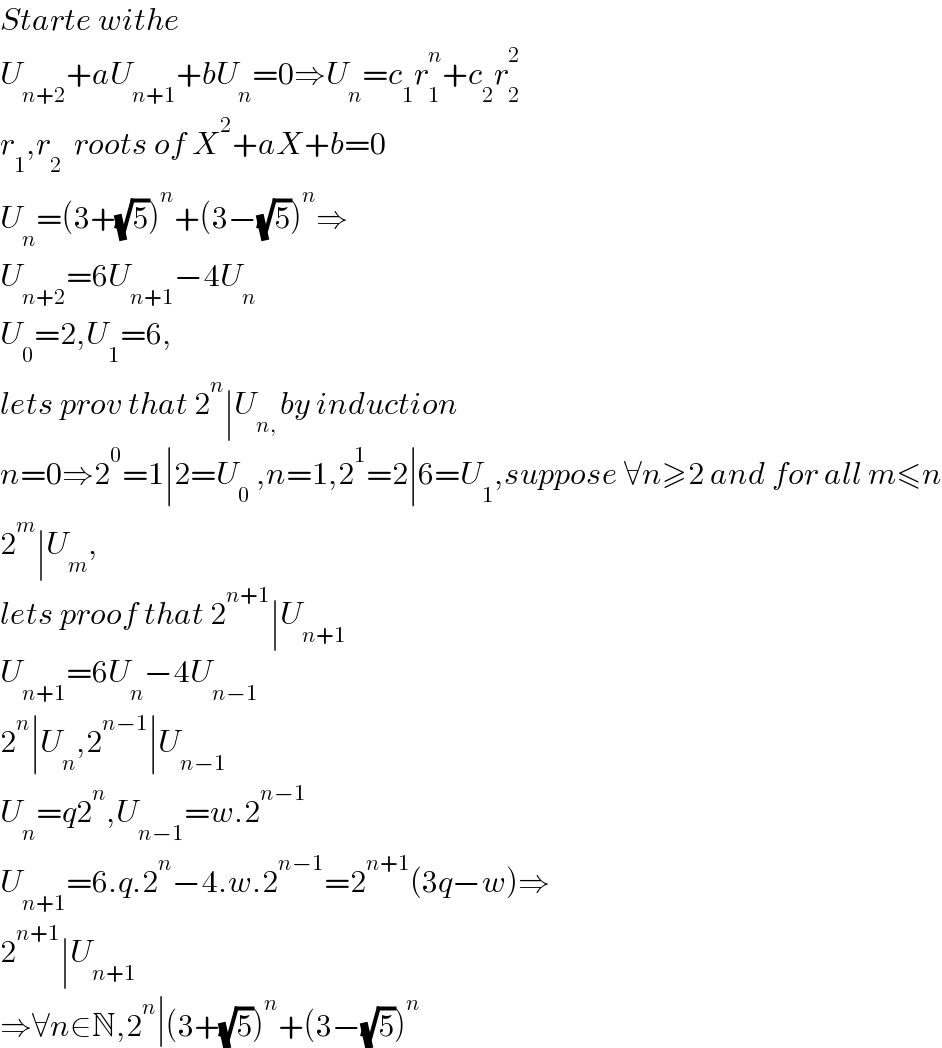
Starte withe U_(n+2) +aU_(n+1) +bU_n =0⇒U_n =c_1 r_1 ^n +c_2 r_2 ^2 r_1 ,r_2 roots of X^2 +aX+b=0 U_n =(3+(√5))^n +(3−(√5))^n ⇒ U_(n+2) =6U_(n+1) −4U_n U_0 =2,U_1 =6, lets prov that 2^n ∣U_(n, ) by induction n=0⇒2^0 =1∣2=U_0 ,n=1,2^1 =2∣6=U_1 ,suppose ∀n≥2 and for all m≤n 2^m ∣U_m , lets proof that 2^(n+1) ∣U_(n+1) U_(n+1) =6U_n −4U_(n−1) 2^n ∣U_n ,2^(n−1) ∣U_(n−1) U_n =q2^n ,U_(n−1) =w.2^(n−1) U_(n+1) =6.q.2^n −4.w.2^(n−1) =2^(n+1) (3q−w)⇒ 2^(n+1) ∣U_(n+1) ⇒∀n∈N,2^n ∣(3+(√5))^n +(3−(√5))^n

$${Starte}\:{withe} \\ $$$${U}_{{n}+\mathrm{2}} +{aU}_{{n}+\mathrm{1}} +{bU}_{{n}} =\mathrm{0}\Rightarrow{U}_{{n}} ={c}_{\mathrm{1}} {r}_{\mathrm{1}} ^{{n}} +{c}_{\mathrm{2}} {r}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${r}_{\mathrm{1}} ,{r}_{\mathrm{2}} \:\:{roots}\:{of}\:{X}^{\mathrm{2}} +{aX}+{b}=\mathrm{0} \\ $$$${U}_{{n}} =\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)^{{n}} +\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)^{{n}} \Rightarrow \\ $$$${U}_{{n}+\mathrm{2}} =\mathrm{6}{U}_{{n}+\mathrm{1}} −\mathrm{4}{U}_{{n}} \\ $$$${U}_{\mathrm{0}} =\mathrm{2},{U}_{\mathrm{1}} =\mathrm{6}, \\ $$$${lets}\:{prov}\:{that}\:\mathrm{2}^{{n}} \mid{U}_{{n},\:} {by}\:{induction} \\ $$$${n}=\mathrm{0}\Rightarrow\mathrm{2}^{\mathrm{0}} =\mathrm{1}\mid\mathrm{2}={U}_{\mathrm{0}} \:,{n}=\mathrm{1},\mathrm{2}^{\mathrm{1}} =\mathrm{2}\mid\mathrm{6}={U}_{\mathrm{1}} ,{suppose}\:\forall{n}\geqslant\mathrm{2}\:{and}\:{for}\:{all}\:{m}\leqslant{n} \\ $$$$\mathrm{2}^{{m}} \mid{U}_{{m}} , \\ $$$${lets}\:{proof}\:{that}\:\mathrm{2}^{{n}+\mathrm{1}} \mid{U}_{{n}+\mathrm{1}} \\ $$$${U}_{{n}+\mathrm{1}} =\mathrm{6}{U}_{{n}} −\mathrm{4}{U}_{{n}−\mathrm{1}} \\ $$$$\mathrm{2}^{{n}} \mid{U}_{{n}} ,\mathrm{2}^{{n}−\mathrm{1}} \mid{U}_{{n}−\mathrm{1}} \\ $$$${U}_{{n}} ={q}\mathrm{2}^{{n}} ,{U}_{{n}−\mathrm{1}} ={w}.\mathrm{2}^{{n}−\mathrm{1}} \\ $$$${U}_{{n}+\mathrm{1}} =\mathrm{6}.{q}.\mathrm{2}^{{n}} −\mathrm{4}.{w}.\mathrm{2}^{{n}−\mathrm{1}} =\mathrm{2}^{{n}+\mathrm{1}} \left(\mathrm{3}{q}−{w}\right)\Rightarrow \\ $$$$\mathrm{2}^{{n}+\mathrm{1}} \mid{U}_{{n}+\mathrm{1}} \\ $$$$\Rightarrow\forall{n}\in\mathbb{N},\mathrm{2}^{{n}} \mid\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)^{{n}} +\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)^{{n}} \\ $$

Commented by KONE last updated on 14/Dec/21

merci merci bien que Dieu vlus benisse

$${merci}\:{merci}\:{bien}\:{que}\:{Dieu}\:{vlus}\:{benisse} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com