
Question Number 160953 by SANOGO last updated on 09/Dec/21
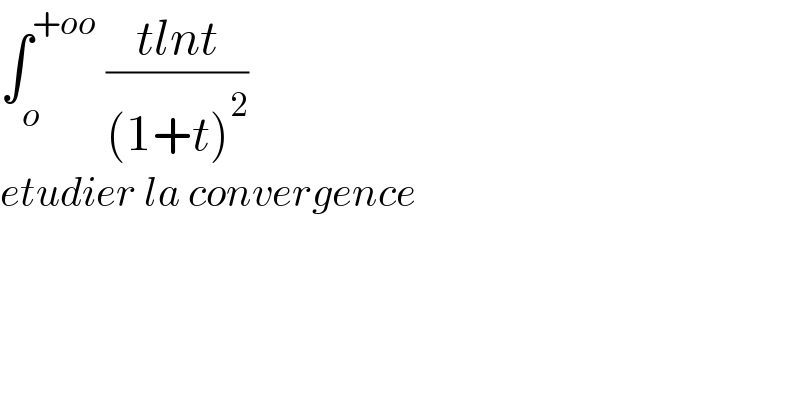
$$\int_{{o}} ^{+{oo}} \:\frac{{tlnt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\:\:\:\: \\ $$$${etudier}\:{la}\:{convergence} \\ $$
Answered by ArielVyny last updated on 10/Dec/21
![f(t)=((tln(t))/((1+t)^2 )) t>0 Df=]0;+∞[ lim f(t)_(t→+∞) =lim((tlnt)/((1+t)^2 ))∼lim(t/t^2 ) =0(par croissance compare) lim f(t)_(t→0) =lim_(t→0) ((tlnt)/((1+t)^2 ))=0 donc f admet prolongement par continuite en 0 conclusion lim f(t)_(t→+∞) =0;lim f(t)_(t→0) =0 d′ou ∫_0 ^∞ ((tlnt)/((1+t)^2 ))dt ∫_a ^b f(t)dt converge avec a et appartenant [−∞;+∞] si f est continue sur l′inerval et lim f(t)_(t→a) et lim f(t)_(t→b) existent](Q161018.png)
$$\left.{f}\left({t}\right)=\frac{{tln}\left({t}\right)}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\:\:{t}>\mathrm{0}\:{Df}=\right]\mathrm{0};+\infty\left[\right. \\ $$$${lim}\:{f}\left({t}\right)_{{t}\rightarrow+\infty} ={lim}\frac{{tlnt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\sim{lim}\frac{{t}}{{t}^{\mathrm{2}} }\:=\mathrm{0}\left({par}\:{croissance}\:{compare}\right) \\ $$$${lim}\:{f}\left({t}\right)_{{t}\rightarrow\mathrm{0}} ={lim}_{{t}\rightarrow\mathrm{0}} \frac{{tlnt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$${donc}\:{f}\:{admet}\:{prolongement}\:{par}\:{continuite} \\ $$$${en}\:\mathrm{0}\: \\ $$$${conclusion}\:{lim}\:{f}\left({t}\right)_{{t}\rightarrow+\infty} =\mathrm{0};{lim}\:{f}\left({t}\right)_{{t}\rightarrow\mathrm{0}} =\mathrm{0} \\ $$$${d}'{ou}\:\int_{\mathrm{0}} ^{\infty} \frac{{tlnt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$$$\int_{{a}} ^{{b}} {f}\left({t}\right){dt}\:{converge}\:{avec}\:{a}\:{et}\:{appartenant}\: \\ $$$$\left[−\infty;+\infty\right]\:{si}\:{f}\:{est}\:{continue}\:{sur}\:{l}'{inerval}\:{et} \\ $$$${lim}\:{f}\left({t}\right)_{{t}\rightarrow{a}} \:{et}\:{lim}\:{f}\left({t}\right)_{{t}\rightarrow{b}} \:{existent} \\ $$
Commented by SANOGO last updated on 11/Dec/21
$${merci}\:{bien} \\ $$
