
Question and Answers Forum
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 160980 by cortano last updated on 10/Dec/21
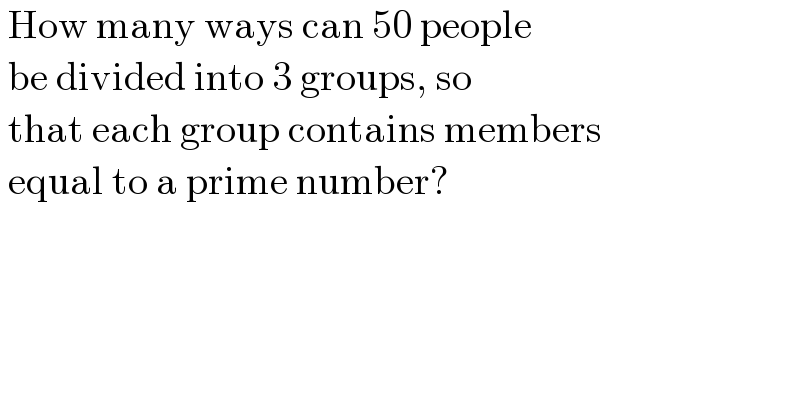
Answered by Rasheed.Sindhi last updated on 10/Dec/21

Commented by cortano last updated on 10/Dec/21

Commented by Rasheed.Sindhi last updated on 10/Dec/21

Commented by bobhans last updated on 10/Dec/21
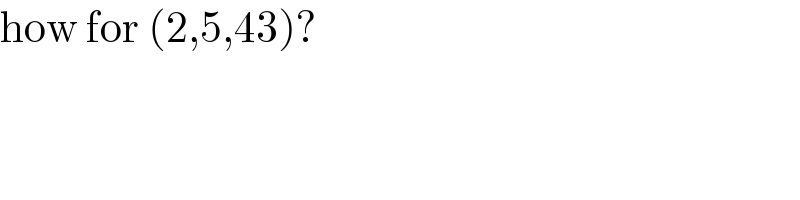
Commented by Rasheed.Sindhi last updated on 10/Dec/21
Answered by mr W last updated on 10/Dec/21
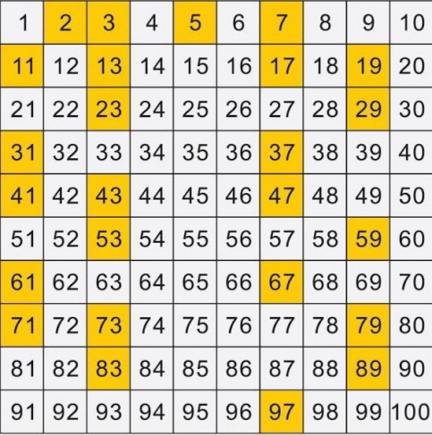
Commented by mr W last updated on 10/Dec/21

Commented by Tawa11 last updated on 10/Dec/21

Commented by cortano last updated on 10/Dec/21

