Question and Answers Forum
Question Number 161285 by cortano last updated on 15/Dec/21
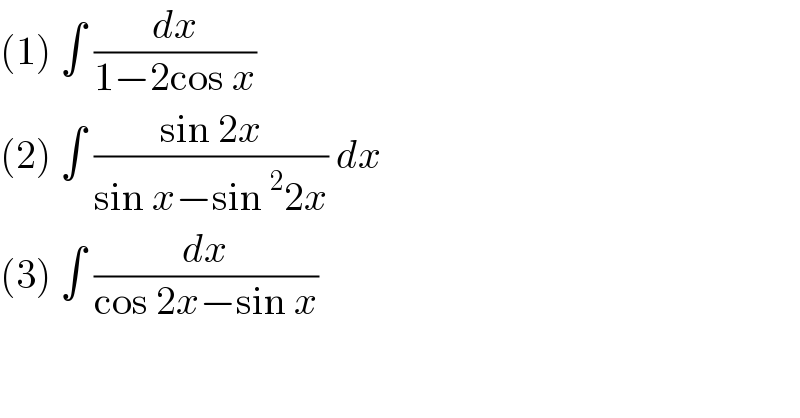
Answered by bobhans last updated on 15/Dec/21
![(1) ∫ (dx/(1−2cos x)) = ∫ (dx/(1−2(2cos^2 ((x/2))−1))) = ∫ (dx/(3−4cos^2 ((x/2)))) ; [tan (x/2)=t → { ((cos (x/2)=(1/( (√(1+t^2 )))))),((dx=(2/(1+t^2 )) dt)) :}] = ∫ (2/(1+t^2 )) ((1/(3−(4/(1+t^2 )))))dt = ∫ (2/(3t^2 −1)) dt = ∫ (2/((t(√3)−1)(t(√3)+1))) dt = ∫ ((1/(t(√3)−1)) −(1/(t(√3)+1)))dt = (1/( (√3))) ln ∣t(√3)−1∣−(1/( (√3))) ln ∣t(√3)+1∣ + c = (1/( (√3))) ln ∣(((√3) tan ((x/2))−1)/( (√3) tan ((x/2))+1))∣ + c](Q161287.png)
Answered by bobhans last updated on 17/Dec/21
![(Q) ∫ (dx/(cos 2x−sin x)) =? (⇒ ) ∫ (dx/(1−2sin^2 x−sin x)) = ∫ (dx/(−2sin^2 x−sin x+1)) =−∫ (dx/(2sin^2 x+sin x−1)) = −∫ (dx/((2sin x−1)(sin x+1))) = −(1/3)∫ ((2/(2sin x−1))−(1/(sin x+1)))dx [ tan (x/2)=u → { ((sin x = ((2u)/(1+u^2 )))),((dx=(2/(1+u^2 )))) :} ] I_1 =−(2/3) ∫ (2/(1+u^2 )) .(1/(((4u)/(1+u^2 ))−1)) du I_1 = −(4/3)∫ (du/(4u−u^2 −1))= (4/3)∫ (du/((u−2)^2 −5)) [ let u−2 =(√5) sec t ] I_1 = (4/3) ∫ (((√5) sec t tan t dt)/(5 tan^2 t))=(4/(3(√5)))∫csc t dt I_1 = (4/(3(√5))) ln ∣ csc t−cot t ∣ + c_(1 ) I_2 = (1/3)∫ (dx/(sin x+1)) = (1/3)∫ (2/(1+u^2 )).(1/(((2u)/(1+u^2 ))+1)) du I_2 = (2/3)∫ (du/((u+1)^2 )) = (2/3)∫ (u+1)^(−2) du I_2 = −(2/(3(u+1))) + c_2 =−(2/(3(tan ((x/2))+1))) + c_2 ∴ I = I_1 +I_2](Q161290.png)
Answered by Ar Brandon last updated on 15/Dec/21
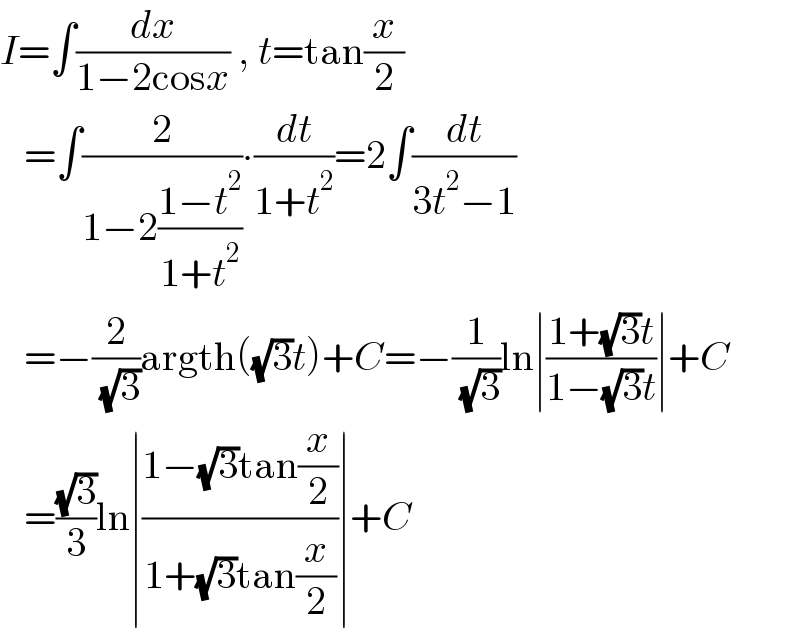
Answered by Ar Brandon last updated on 15/Dec/21
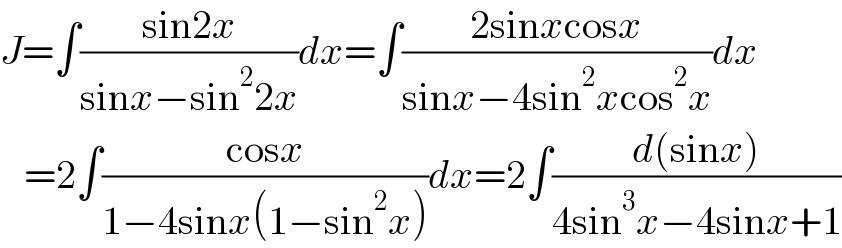
Answered by Tyller last updated on 19/Dec/21