Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 161366 by mr W last updated on 17/Dec/21

[similar question reposted] if a+(3/b)=b+(3/c)=c+(3/a) with a≠b≠c and a,b,c ∈ R. find (abc)^2 =?

$$\left[{similar}\:{question}\:{reposted}\right] \\ $$$${if}\:{a}+\frac{\mathrm{3}}{{b}}={b}+\frac{\mathrm{3}}{{c}}={c}+\frac{\mathrm{3}}{{a}}\:{with}\:{a}\neq{b}\neq{c} \\ $$$${and}\:{a},{b},{c}\:\in\:\mathbb{R}.\:{find}\:\left({abc}\right)^{\mathrm{2}} =? \\ $$

Answered by 1549442205PVT last updated on 18/Dec/21

From the hypothesis we have: a+(3/b)=c+(3/a)⇒c=((a^2 −3)/a)+(3/b)(1)⇒(3/c)=((3ab)/(a^2 b+3a−3b)) ⇒a+(3/b)=b+((3ab)/(a^2 b+3a−3b))⇒((ab+3−b^2 )/b)=((3ab)/(a^2 b+3a−3b)) ⇔a^3 b^2 +3a^2 b−a^2 b^3 +3a^2 b+9a−3ab^2 −3ab^2 −9b+3b^3 =3ab^2 After simplifycation we obtain a^3 b^2 −(b^3 −6b)a^2 −(9b^2 −9)a+3b^3 −9b =(a−b)(a^2 b^2 +6ab−3b^2 +9)=0.Since a≠b ,we get a^2 b^2 +6ab−3b^2 +9=0 ⇔(a^2 −3)b^2 +6ab+9=0. •if a^2 −3=0⇔a=±(√3) then b=((−3)/(±2(√3)))=((∓(√3))/2) ⇒c=∓2(√3)⇒abc=±3(√3) ⇒(abc)^2 =27 •if a^2 −3≠0.Then △′=9a^2 −9a^2 +27=27,so b=((−3a±3(√3))/(a^2 −3)).Hence from(1)weget bc=3+((a^2 −3)/a).b=3+((−3a±3(√3))/a) ⇒abc=3a−3a±3(√3)=±3(√3) ⇒(abc)^2 =27

$${From}\:{the}\:{hypothesis}\:{we}\:{have}: \\ $$$${a}+\frac{\mathrm{3}}{{b}}={c}+\frac{\mathrm{3}}{{a}}\Rightarrow{c}=\frac{{a}^{\mathrm{2}} −\mathrm{3}}{{a}}+\frac{\mathrm{3}}{{b}}\left(\mathrm{1}\right)\Rightarrow\frac{\mathrm{3}}{{c}}=\frac{\mathrm{3}{ab}}{{a}^{\mathrm{2}} {b}+\mathrm{3}{a}−\mathrm{3}{b}} \\ $$$$\Rightarrow{a}+\frac{\mathrm{3}}{{b}}={b}+\frac{\mathrm{3}{ab}}{{a}^{\mathrm{2}} {b}+\mathrm{3}{a}−\mathrm{3}{b}}\Rightarrow\frac{{ab}+\mathrm{3}−{b}^{\mathrm{2}} }{{b}}=\frac{\mathrm{3}{ab}}{{a}^{\mathrm{2}} {b}+\mathrm{3}{a}−\mathrm{3}{b}} \\ $$$$\Leftrightarrow{a}^{\mathrm{3}} {b}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} {b}−{a}^{\mathrm{2}} {b}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} {b}+\mathrm{9}{a}−\mathrm{3}{ab}^{\mathrm{2}} −\mathrm{3}{ab}^{\mathrm{2}} −\mathrm{9}{b}+\mathrm{3}{b}^{\mathrm{3}} =\mathrm{3}{ab}^{\mathrm{2}} \\ $$$${After}\:{simplifycation}\:{we}\:{obtain} \\ $$$${a}^{\mathrm{3}} {b}^{\mathrm{2}} −\left({b}^{\mathrm{3}} −\mathrm{6}{b}\right){a}^{\mathrm{2}} −\left(\mathrm{9}{b}^{\mathrm{2}} −\mathrm{9}\right){a}+\mathrm{3}{b}^{\mathrm{3}} −\mathrm{9}{b} \\ $$$$=\left({a}−{b}\right)\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{6}{ab}−\mathrm{3}{b}^{\mathrm{2}} +\mathrm{9}\right)=\mathrm{0}.{Since}\:{a}\neq{b} \\ $$$$,{we}\:{get}\:{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{6}{ab}−\mathrm{3}{b}^{\mathrm{2}} +\mathrm{9}=\mathrm{0} \\ $$$$\Leftrightarrow\left({a}^{\mathrm{2}} −\mathrm{3}\right){b}^{\mathrm{2}} +\mathrm{6}{ab}+\mathrm{9}=\mathrm{0}. \\ $$$$\bullet{if}\:{a}^{\mathrm{2}} −\mathrm{3}=\mathrm{0}\Leftrightarrow{a}=\pm\sqrt{\mathrm{3}}\:{then}\:{b}=\frac{−\mathrm{3}}{\pm\mathrm{2}\sqrt{\mathrm{3}}}=\frac{\mp\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow{c}=\mp\mathrm{2}\sqrt{\mathrm{3}}\Rightarrow{abc}=\pm\mathrm{3}\sqrt{\mathrm{3}}\:\Rightarrow\left({abc}\right)^{\mathrm{2}} =\mathrm{27} \\ $$$$\bullet{if}\:{a}^{\mathrm{2}} −\mathrm{3}\neq\mathrm{0}.{Then}\:\bigtriangleup'=\mathrm{9}{a}^{\mathrm{2}} −\mathrm{9}{a}^{\mathrm{2}} +\mathrm{27}=\mathrm{27},{so} \\ $$$${b}=\frac{−\mathrm{3}{a}\pm\mathrm{3}\sqrt{\mathrm{3}}}{{a}^{\mathrm{2}} −\mathrm{3}}.{Hence}\:{from}\left(\mathrm{1}\right){weget} \\ $$$${bc}=\mathrm{3}+\frac{{a}^{\mathrm{2}} −\mathrm{3}}{{a}}.{b}=\mathrm{3}+\frac{−\mathrm{3}{a}\pm\mathrm{3}\sqrt{\mathrm{3}}}{{a}} \\ $$$$\Rightarrow{abc}=\mathrm{3}{a}−\mathrm{3}{a}\pm\mathrm{3}\sqrt{\mathrm{3}}=\pm\mathrm{3}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\left({abc}\right)^{\mathrm{2}} =\mathrm{27} \\ $$$$ \\ $$

Commented by mr W last updated on 17/Dec/21

thanks sir!

$${thanks}\:{sir}! \\ $$

Commented by 1549442205PVT last updated on 18/Dec/21

Thank you Sir Mr.W ,i mistake and corrected

$${Thank}\:{you}\:{Sir}\:{Mr}.{W}\:,{i}\:{mistake}\:{and}\:{corrected} \\ $$

Answered by mr W last updated on 17/Dec/21

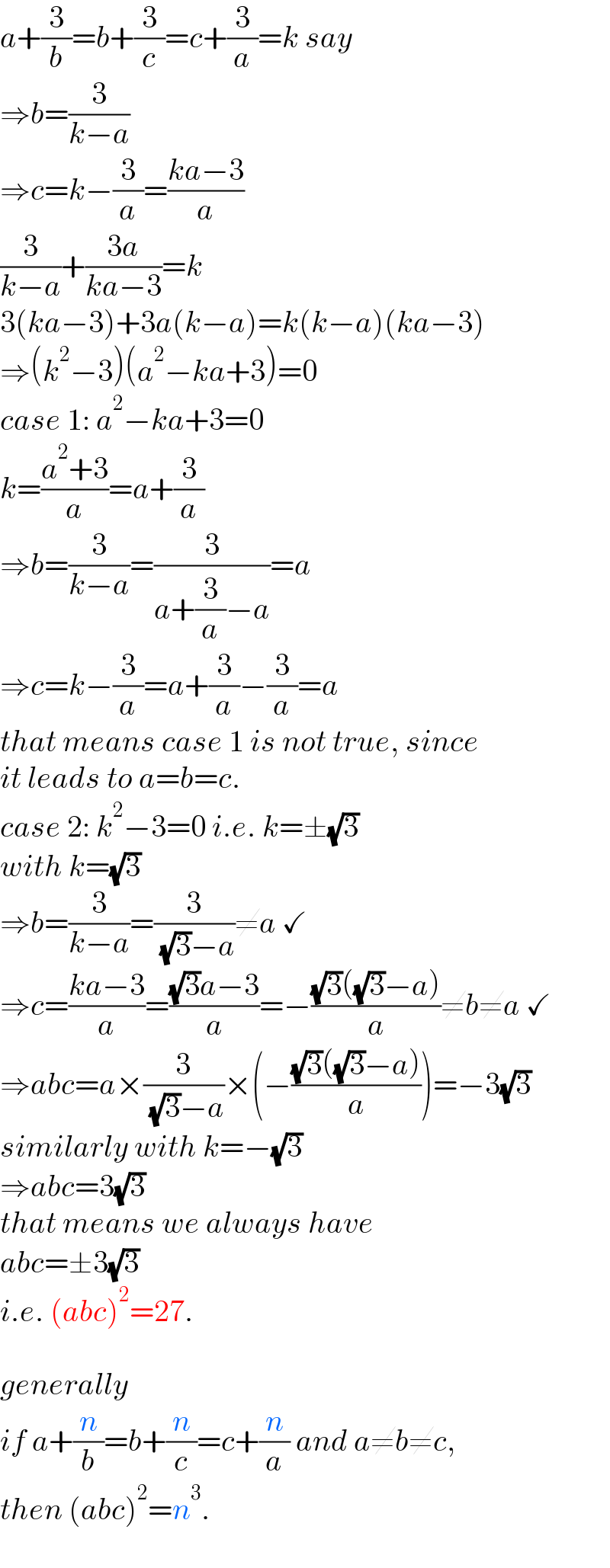
a+(3/b)=b+(3/c)=c+(3/a)=k say ⇒b=(3/(k−a)) ⇒c=k−(3/a)=((ka−3)/a) (3/(k−a))+((3a)/(ka−3))=k 3(ka−3)+3a(k−a)=k(k−a)(ka−3) ⇒(k^2 −3)(a^2 −ka+3)=0 case 1: a^2 −ka+3=0 k=((a^2 +3)/a)=a+(3/a) ⇒b=(3/(k−a))=(3/(a+(3/a)−a))=a ⇒c=k−(3/a)=a+(3/a)−(3/a)=a that means case 1 is not true, since it leads to a=b=c. case 2: k^2 −3=0 i.e. k=±(√3) with k=(√3) ⇒b=(3/(k−a))=(3/( (√3)−a))≠a ✓ ⇒c=((ka−3)/a)=(((√3)a−3)/a)=−(((√3)((√3)−a))/a)≠b≠a ✓ ⇒abc=a×(3/( (√3)−a))×(−(((√3)((√3)−a))/a))=−3(√3) similarly with k=−(√3) ⇒abc=3(√3) that means we always have abc=±3(√3) i.e. (abc)^2 =27. generally if a+(n/b)=b+(n/c)=c+(n/a) and a≠b≠c, then (abc)^2 =n^3 .

$${a}+\frac{\mathrm{3}}{{b}}={b}+\frac{\mathrm{3}}{{c}}={c}+\frac{\mathrm{3}}{{a}}={k}\:{say} \\ $$$$\Rightarrow{b}=\frac{\mathrm{3}}{{k}−{a}} \\ $$$$\Rightarrow{c}={k}−\frac{\mathrm{3}}{{a}}=\frac{{ka}−\mathrm{3}}{{a}} \\ $$$$\frac{\mathrm{3}}{{k}−{a}}+\frac{\mathrm{3}{a}}{{ka}−\mathrm{3}}={k} \\ $$$$\mathrm{3}\left({ka}−\mathrm{3}\right)+\mathrm{3}{a}\left({k}−{a}\right)={k}\left({k}−{a}\right)\left({ka}−\mathrm{3}\right) \\ $$$$\Rightarrow\left({k}^{\mathrm{2}} −\mathrm{3}\right)\left({a}^{\mathrm{2}} −{ka}+\mathrm{3}\right)=\mathrm{0} \\ $$$${case}\:\mathrm{1}:\:{a}^{\mathrm{2}} −{ka}+\mathrm{3}=\mathrm{0} \\ $$$${k}=\frac{{a}^{\mathrm{2}} +\mathrm{3}}{{a}}={a}+\frac{\mathrm{3}}{{a}} \\ $$$$\Rightarrow{b}=\frac{\mathrm{3}}{{k}−{a}}=\frac{\mathrm{3}}{{a}+\frac{\mathrm{3}}{{a}}−{a}}={a} \\ $$$$\Rightarrow{c}={k}−\frac{\mathrm{3}}{{a}}={a}+\frac{\mathrm{3}}{{a}}−\frac{\mathrm{3}}{{a}}={a} \\ $$$${that}\:{means}\:{case}\:\mathrm{1}\:{is}\:{not}\:{true},\:{since} \\ $$$${it}\:{leads}\:{to}\:{a}={b}={c}. \\ $$$${case}\:\mathrm{2}:\:{k}^{\mathrm{2}} −\mathrm{3}=\mathrm{0}\:{i}.{e}.\:{k}=\pm\sqrt{\mathrm{3}} \\ $$$${with}\:{k}=\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{b}=\frac{\mathrm{3}}{{k}−{a}}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{3}}−{a}}\neq{a}\:\checkmark \\ $$$$\Rightarrow{c}=\frac{{ka}−\mathrm{3}}{{a}}=\frac{\sqrt{\mathrm{3}}{a}−\mathrm{3}}{{a}}=−\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}−{a}\right)}{{a}}\neq{b}\neq{a}\:\checkmark \\ $$$$\Rightarrow{abc}={a}×\frac{\mathrm{3}}{\:\sqrt{\mathrm{3}}−{a}}×\left(−\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}−{a}\right)}{{a}}\right)=−\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${similarly}\:{with}\:{k}=−\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{abc}=\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${that}\:{means}\:{we}\:{always}\:{have}\: \\ $$$${abc}=\pm\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${i}.{e}.\:\left({abc}\right)^{\mathrm{2}} =\mathrm{27}. \\ $$$$ \\ $$$${generally} \\ $$$${if}\:{a}+\frac{{n}}{{b}}={b}+\frac{{n}}{{c}}={c}+\frac{{n}}{{a}}\:{and}\:{a}\neq{b}\neq{c}, \\ $$$${then}\:\left({abc}\right)^{\mathrm{2}} ={n}^{\mathrm{3}} . \\ $$

Commented by Tawa11 last updated on 17/Dec/21

Great sir.

$$\mathrm{Great}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com