Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 16140 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 18/Jun/17

Answered by ajfour last updated on 18/Jun/17

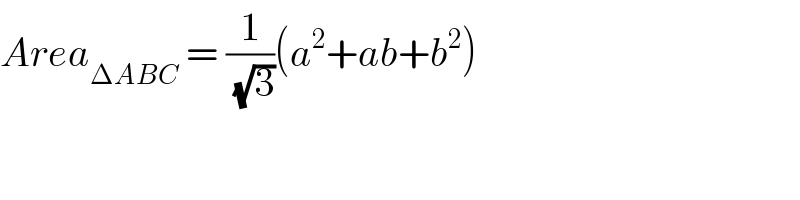
Area_(ΔABC) = (1/(√3))(a^2 +ab+b^2 )

$${Area}_{\Delta{ABC}} \:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)\: \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 18/Jun/17

thank you so much mr Ajfour.nice method.i love it. can we use this solution for Q.15969?

$${thank}\:{you}\:{so}\:{much}\:{mr}\:{Ajfour}.{nice} \\ $$$${method}.{i}\:{love}\:{it}. \\ $$$${can}\:{we}\:{use}\:{this}\:{solution}\:{for}\:{Q}.\mathrm{15969}? \\ $$

Commented by ajfour last updated on 18/Jun/17

Commented by ajfour last updated on 18/Jun/17

ssin θ = a ssin ((π/3)−θ) = b s(((√3)/2)cos θ−(1/2)sin θ) = b (√3)scos θ−ssin θ = 2b (√3)(√(s^2 −a^2 )) = a+2b 3(s^2 −a^2 ) = (a+2b)^2 s^2 = a^2 +(((a+2b)^2 )/3) A = ((√3)/4)[a^2 +(((a+2b)^2 )/3) ] = (1/(4(√3))) (4a^2 +4b^2 +4ab) = (1/(√3))(a^2 +ab+b^2 ) .

$$\:\:\:{s}\mathrm{sin}\:\theta\:=\:{a} \\ $$$$\:\:\:{s}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\theta\right)\:=\:{b} \\ $$$$\:\:\:{s}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:\theta−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\theta\right)\:=\:{b} \\ $$$$\:\:\:\sqrt{\mathrm{3}}{s}\mathrm{cos}\:\theta−{s}\mathrm{sin}\:\theta\:=\:\mathrm{2}{b} \\ $$$$\:\:\:\sqrt{\mathrm{3}}\sqrt{{s}^{\mathrm{2}} −{a}^{\mathrm{2}} }\:=\:{a}+\mathrm{2}{b} \\ $$$$\:\:\:\mathrm{3}\left({s}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:=\:\left({a}+\mathrm{2}{b}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{s}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} +\frac{\left({a}+\mathrm{2}{b}\right)^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\:\:\:{A}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left[{a}^{\mathrm{2}} +\frac{\left({a}+\mathrm{2}{b}\right)^{\mathrm{2}} }{\mathrm{3}}\:\right] \\ $$$$\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}\:\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{4}{b}^{\mathrm{2}} +\mathrm{4}{ab}\right) \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)\:. \\ $$

Answered by mrW1 last updated on 18/Jun/17

When we fix the first vertex of an equilateral on one line, let′s say on line 2, and lay the second vertex variably on an other line, let′s say on line 1, the track of the third convex is a straight line. The inter− section point of this line with the third line is the second convex of the equi− lateral triangle which we are searching. Thus we can “draw” the requested equi− lateral triangle in following way. We fix the pint B on line 2. On line 1 we select at least two points P_1 and P_2 . With BP_1 and BP_2 as base we construct in the same direction equilateral triangles BP_1 Q_1 and BP_2 Q_2 . We connect Q_1 and Q_2 . This new line intersects with line 3 at point C. BC is then the one side of the requested equilateral triangle. The point A on line 1 can be then easily determined.

$$\mathrm{When}\:\mathrm{we}\:\mathrm{fix}\:\mathrm{the}\:\mathrm{first}\:\mathrm{vertex}\:\mathrm{of}\:\mathrm{an}\:\mathrm{equilateral} \\ $$$$\mathrm{on}\:\mathrm{one}\:\mathrm{line},\:\mathrm{let}'\mathrm{s}\:\mathrm{say}\:\mathrm{on}\:\mathrm{line}\:\mathrm{2},\:\mathrm{and}\:\mathrm{lay} \\ $$$$\mathrm{the}\:\mathrm{second}\:\mathrm{vertex}\:\mathrm{variably}\:\mathrm{on}\:\mathrm{an}\:\mathrm{other}\:\mathrm{line},\:\mathrm{let}'\mathrm{s} \\ $$$$\mathrm{say}\:\mathrm{on}\:\mathrm{line}\:\mathrm{1},\:\mathrm{the}\:\mathrm{track}\:\mathrm{of}\:\mathrm{the}\:\mathrm{third}\: \\ $$$$\mathrm{convex}\:\mathrm{is}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}.\:\mathrm{The}\:\mathrm{inter}− \\ $$$$\mathrm{section}\:\mathrm{point}\:\mathrm{of}\:\mathrm{this}\:\mathrm{line}\:\mathrm{with}\:\mathrm{the}\:\mathrm{third} \\ $$$$\mathrm{line}\:\mathrm{is}\:\mathrm{the}\:\mathrm{second}\:\mathrm{convex}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equi}− \\ $$$$\mathrm{lateral}\:\mathrm{triangle}\:\mathrm{which}\:\mathrm{we}\:\mathrm{are}\:\mathrm{searching}. \\ $$$$ \\ $$$$\mathrm{Thus}\:\mathrm{we}\:\mathrm{can}\:``\mathrm{draw}''\:\mathrm{the}\:\mathrm{requested}\:\mathrm{equi}− \\ $$$$\mathrm{lateral}\:\mathrm{triangle}\:\mathrm{in}\:\mathrm{following}\:\mathrm{way}. \\ $$$$\mathrm{We}\:\mathrm{fix}\:\mathrm{the}\:\mathrm{pint}\:\mathrm{B}\:\mathrm{on}\:\mathrm{line}\:\mathrm{2}. \\ $$$$\mathrm{On}\:\mathrm{line}\:\mathrm{1}\:\mathrm{we}\:\mathrm{select}\:\mathrm{at}\:\mathrm{least}\:\mathrm{two}\:\mathrm{points} \\ $$$$\mathrm{P}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{P}_{\mathrm{2}} .\:\mathrm{With}\:\mathrm{BP}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{BP}_{\mathrm{2}} \:\mathrm{as}\:\mathrm{base} \\ $$$$\mathrm{we}\:\mathrm{construct}\:\:\mathrm{in}\:\mathrm{the}\:\mathrm{same}\:\mathrm{direction} \\ $$$$\mathrm{equilateral}\:\mathrm{triangles}\:\mathrm{BP}_{\mathrm{1}} \mathrm{Q}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{BP}_{\mathrm{2}} \mathrm{Q}_{\mathrm{2}} . \\ $$$$\mathrm{We}\:\mathrm{connect}\:\mathrm{Q}_{\mathrm{1}} \mathrm{and}\:\mathrm{Q}_{\mathrm{2}} .\:\mathrm{This}\:\mathrm{new}\:\mathrm{line} \\ $$$$\mathrm{intersects}\:\mathrm{with}\:\mathrm{line}\:\mathrm{3}\:\mathrm{at}\:\mathrm{point}\:\mathrm{C}. \\ $$$$\mathrm{BC}\:\mathrm{is}\:\mathrm{then}\:\mathrm{the}\:\mathrm{one}\:\mathrm{side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{requested} \\ $$$$\mathrm{equilateral}\:\mathrm{triangle}.\:\mathrm{The}\:\mathrm{point}\:\mathrm{A}\:\mathrm{on} \\ $$$$\mathrm{line}\:\mathrm{1}\:\mathrm{can}\:\mathrm{be}\:\mathrm{then}\:\mathrm{easily}\:\mathrm{determined}. \\ $$

Commented by mrW1 last updated on 18/Jun/17

Commented by mrW1 last updated on 18/Jun/17

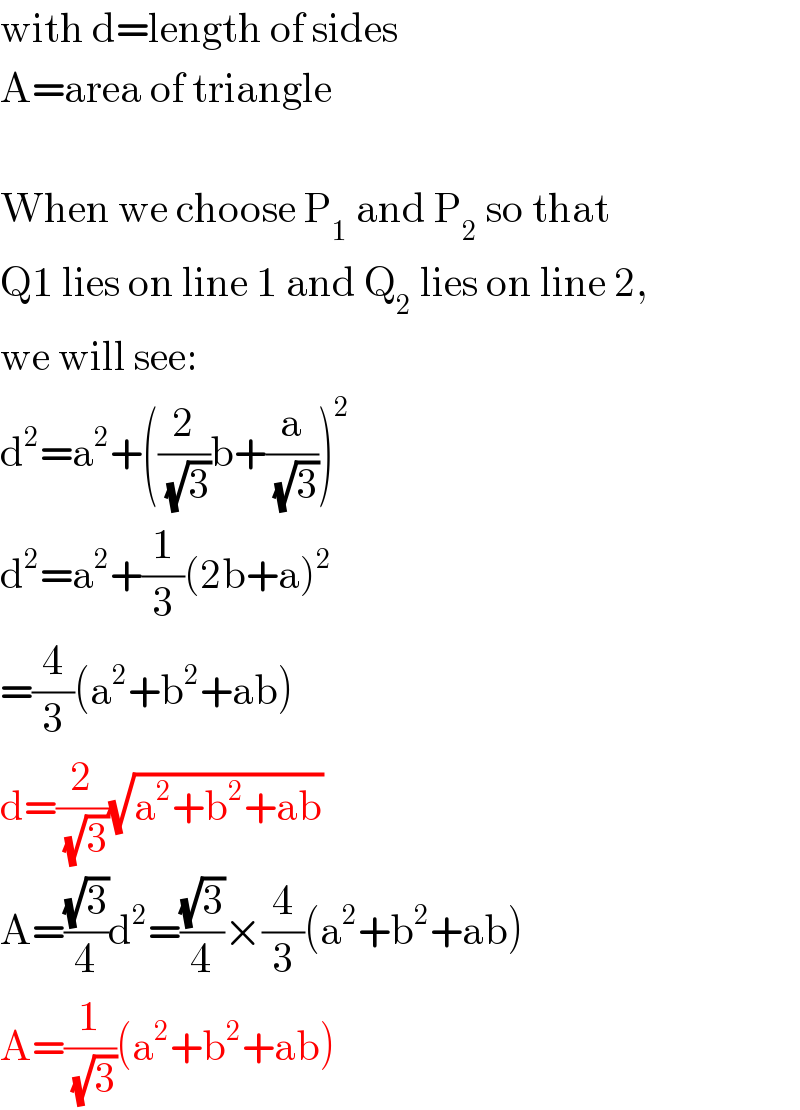
with d=length of sides A=area of triangle When we choose P_1 and P_2 so that Q1 lies on line 1 and Q_2 lies on line 2, we will see: d^2 =a^2 +((2/(√3))b+(a/(√3)))^2 d^2 =a^2 +(1/3)(2b+a)^2 =(4/3)(a^2 +b^2 +ab) d=(2/(√3))(√(a^2 +b^2 +ab)) A=((√3)/4)d^2 =((√3)/4)×(4/3)(a^2 +b^2 +ab) A=(1/(√3))(a^2 +b^2 +ab)

$$\mathrm{with}\:\mathrm{d}=\mathrm{length}\:\mathrm{of}\:\mathrm{sides} \\ $$$$\mathrm{A}=\mathrm{area}\:\mathrm{of}\:\mathrm{triangle} \\ $$$$ \\ $$$$\mathrm{When}\:\mathrm{we}\:\mathrm{choose}\:\mathrm{P}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{P}_{\mathrm{2}} \:\mathrm{so}\:\mathrm{that} \\ $$$$\mathrm{Q1}\:\mathrm{lies}\:\mathrm{on}\:\mathrm{line}\:\mathrm{1}\:\mathrm{and}\:\mathrm{Q}_{\mathrm{2}} \:\mathrm{lies}\:\mathrm{on}\:\mathrm{line}\:\mathrm{2}, \\ $$$$\mathrm{we}\:\mathrm{will}\:\mathrm{see}: \\ $$$$\mathrm{d}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} +\left(\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\mathrm{b}+\frac{\mathrm{a}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} \\ $$$$\mathrm{d}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2b}+\mathrm{a}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{ab}\right) \\ $$$$\mathrm{d}=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{ab}} \\ $$$$\mathrm{A}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\mathrm{d}^{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}×\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{ab}\right) \\ $$$$\mathrm{A}=\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{ab}\right) \\ $$

Commented by RasheedSoomro last updated on 18/Jun/17

MrW1,Mr ajfour & Mr Abu Behi. What a depth in geometry you have!!

$$\mathrm{MrW1},\mathrm{Mr}\:\mathrm{ajfour}\:\&\:\mathrm{Mr}\:\mathrm{Abu}\:\mathrm{Behi}. \\ $$$$\mathrm{What}\:\mathrm{a}\:\mathrm{depth}\:\mathrm{in}\:\mathrm{geometry}\:\mathrm{you}\:\mathrm{have}!! \\ $$

Commented by mrW1 last updated on 18/Jun/17

Thank you sir! Geometry has always been my favorite subject.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}!\:\mathrm{Geometry}\:\mathrm{has}\:\:\mathrm{always} \\ $$$$\mathrm{been}\:\mathrm{my}\:\mathrm{favorite}\:\mathrm{subject}. \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 18/Jun/17

thank you so much dear mrW1.i alwyes enjoy your answers and commenets. god blees you my master. do you read my commenet on mr Ajfour′s answer about using this solution for Q.15969?

$${thank}\:{you}\:{so}\:{much}\:{dear}\:{mrW}\mathrm{1}.{i}\:{alwyes} \\ $$$${enjoy}\:{your}\:{answers}\:{and}\:{commenets}. \\ $$$${god}\:{blees}\:{you}\:{my}\:{master}. \\ $$$${do}\:{you}\:{read}\:{my}\:{commenet}\:{on}\:{mr}\:{Ajfour}'{s} \\ $$$${answer}\:{about}\:{using}\:{this}\:{solution}\:{for} \\ $$$${Q}.\mathrm{15969}? \\ $$$$ \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 18/Jun/17

thank you mr Rasheed.my name is:amir. no one called me as:Abu behi yet.(hahaha)

$${thank}\:{you}\:{mr}\:{Rasheed}.{my}\:{name}\:{is}:{amir}. \\ $$$${no}\:{one}\:{called}\:{me}\:{as}:{Abu}\:{behi}\:{yet}.\left({hahaha}\right) \\ $$

Commented by mrW1 last updated on 18/Jun/17

To abu behi: I have read you comment to Mr. ajfour′s solution. In fact the three−line−problem is similar to the three−circle−problem. But the later is much more complicated. For my solutions I used the same way based on knowledge gained from the graphics. Now we have for both problems the graphical and analytical solutions (formula). I have also added my formula for Q15969. Please have a look at it. Or do you see anything which is in your opinion still not solved yet?

$$\mathrm{To}\:\mathrm{abu}\:\mathrm{behi}: \\ $$$$\:\mathrm{I}\:\mathrm{have}\:\mathrm{read}\:\mathrm{you}\:\mathrm{comment}\:\mathrm{to}\:\mathrm{Mr}. \\ $$$$\mathrm{ajfour}'\mathrm{s}\:\mathrm{solution}. \\ $$$$\mathrm{In}\:\mathrm{fact}\:\mathrm{the}\:\mathrm{three}−\mathrm{line}−\mathrm{problem}\:\mathrm{is} \\ $$$$\mathrm{similar}\:\mathrm{to}\:\mathrm{the}\:\mathrm{three}−\mathrm{circle}−\mathrm{problem}. \\ $$$$\mathrm{But}\:\mathrm{the}\:\mathrm{later}\:\mathrm{is}\:\mathrm{much}\:\mathrm{more}\:\mathrm{complicated}. \\ $$$$\mathrm{For}\:\mathrm{my}\:\mathrm{solutions}\:\mathrm{I}\:\mathrm{used}\:\mathrm{the}\:\mathrm{same}\:\mathrm{way} \\ $$$$\mathrm{based}\:\mathrm{on}\:\mathrm{knowledge}\:\mathrm{gained}\:\mathrm{from}\:\mathrm{the} \\ $$$$\mathrm{graphics}. \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{have}\:\mathrm{for}\:\mathrm{both}\:\mathrm{problems}\:\mathrm{the} \\ $$$$\mathrm{graphical}\:\mathrm{and}\:\mathrm{analytical}\:\mathrm{solutions}\: \\ $$$$\left(\mathrm{formula}\right).\:\mathrm{I}\:\mathrm{have}\:\mathrm{also}\:\mathrm{added}\:\mathrm{my} \\ $$$$\mathrm{formula}\:\mathrm{for}\:\mathrm{Q15969}.\:\mathrm{Please}\:\mathrm{have}\:\mathrm{a} \\ $$$$\mathrm{look}\:\mathrm{at}\:\mathrm{it}. \\ $$$$ \\ $$$$\mathrm{Or}\:\mathrm{do}\:\mathrm{you}\:\mathrm{see}\:\mathrm{anything}\:\mathrm{which}\:\mathrm{is}\:\mathrm{in} \\ $$$$\mathrm{your}\:\mathrm{opinion}\:\mathrm{still}\:\mathrm{not}\:\mathrm{solved}\:\mathrm{yet}? \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 18/Jun/17

dear mrW1.thank you for your attention. no,there is no defference between solutions and evry thing have been solved so nice. but i said that words only such as an idea and no more.

$${dear}\:{mrW}\mathrm{1}.{thank}\:{you}\:{for}\:{your}\:{attention}. \\ $$$${no},{there}\:{is}\:{no}\:{defference}\:{between}\:{solutions} \\ $$$${and}\:{evry}\:{thing}\:{have}\:{been}\:{solved}\:{so} \\ $$$${nice}. \\ $$$${but}\:{i}\:{said}\:{that}\:{words}\:{only}\:{such}\:{as}\:{an} \\ $$$${idea}\:{and}\:{no}\:{more}. \\ $$

Commented by mrW1 last updated on 18/Jun/17

Thank you for all these interesting geometry questions.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{all}\:\mathrm{these}\:\mathrm{interesting} \\ $$$$\mathrm{geometry}\:\mathrm{questions}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com