
Question and Answers Forum
Question Number 161437 by cortano last updated on 17/Dec/21
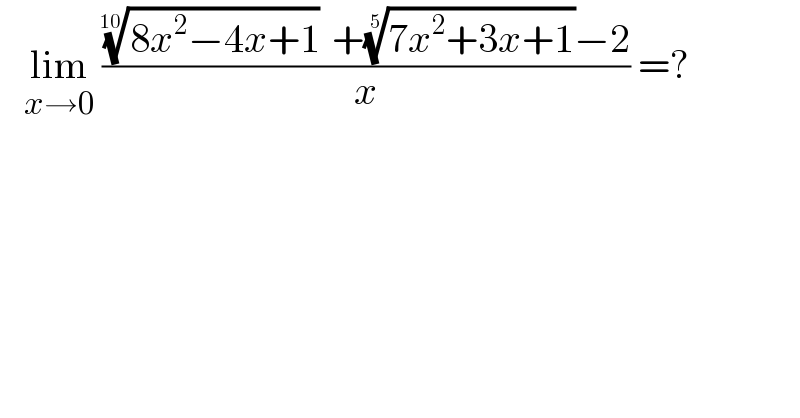
Answered by bobhans last updated on 18/Dec/21
![lim_(x→0) ((((8x^2 −4x+1))^(1/(10)) −1+((7x^2 +3x+1))^(1/5) −1)/x) L_1 = lim_(x→0) (((8x−4)[((8x^2 −4x+1))^(1/(10)) −1 ])/((8x^2 −4x+1)−1)) L_1 = −4×lim_(r→1) ((r−1)/(r^(10) −1)) = −(4/(10)) ; [ r=((8x^2 −4x+1))^(1/(10)) ] L_2 = lim_(x→0) (((7x+3)[((7x^2 +3x+1))^(1/5) −1])/((7x^2 +3x+1)−1)) L_2 = 3×lim_(x→0) ((((7x^2 +3x+1))^(1/5) −1)/((7x^2 +3x+1)−1)) L_2 = 3×lim_(z→1) ((z−1)/(z^5 −1)) = (3/5) ; [ z=((7x^2 +3x+1))^(1/5) ] ∴ L = L_1 +L_2 = −(4/(10))+(3/5) = (2/(10))=(1/5)](Q161440.png)
Answered by mathmax by abdo last updated on 18/Dec/21
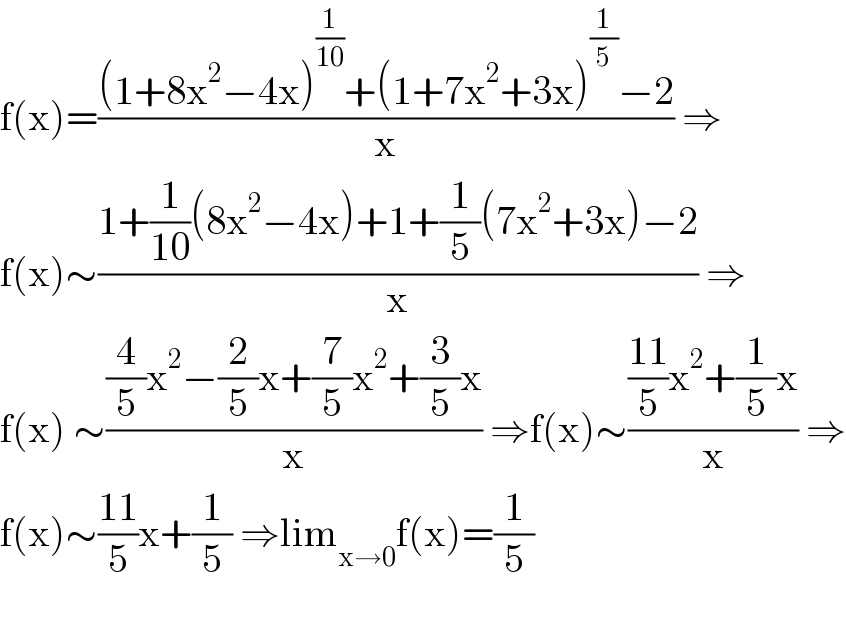
| ||
Question and Answers Forum | ||
Question Number 161437 by cortano last updated on 17/Dec/21 | ||
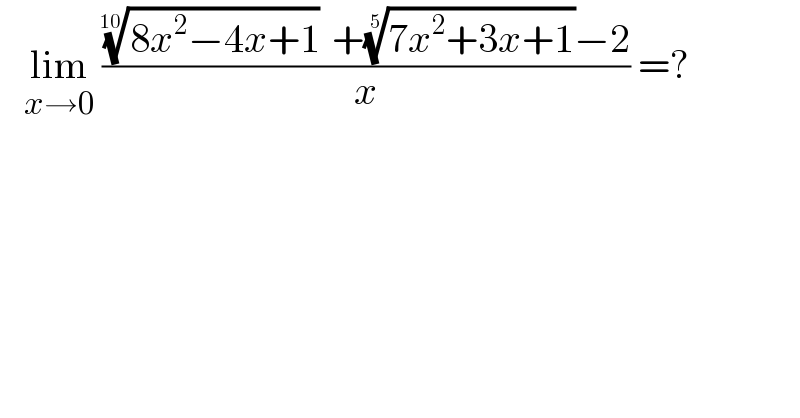 | ||
Answered by bobhans last updated on 18/Dec/21 | ||
![lim_(x→0) ((((8x^2 −4x+1))^(1/(10)) −1+((7x^2 +3x+1))^(1/5) −1)/x) L_1 = lim_(x→0) (((8x−4)[((8x^2 −4x+1))^(1/(10)) −1 ])/((8x^2 −4x+1)−1)) L_1 = −4×lim_(r→1) ((r−1)/(r^(10) −1)) = −(4/(10)) ; [ r=((8x^2 −4x+1))^(1/(10)) ] L_2 = lim_(x→0) (((7x+3)[((7x^2 +3x+1))^(1/5) −1])/((7x^2 +3x+1)−1)) L_2 = 3×lim_(x→0) ((((7x^2 +3x+1))^(1/5) −1)/((7x^2 +3x+1)−1)) L_2 = 3×lim_(z→1) ((z−1)/(z^5 −1)) = (3/5) ; [ z=((7x^2 +3x+1))^(1/5) ] ∴ L = L_1 +L_2 = −(4/(10))+(3/5) = (2/(10))=(1/5)](Q161440.png) | ||
| ||
Answered by mathmax by abdo last updated on 18/Dec/21 | ||
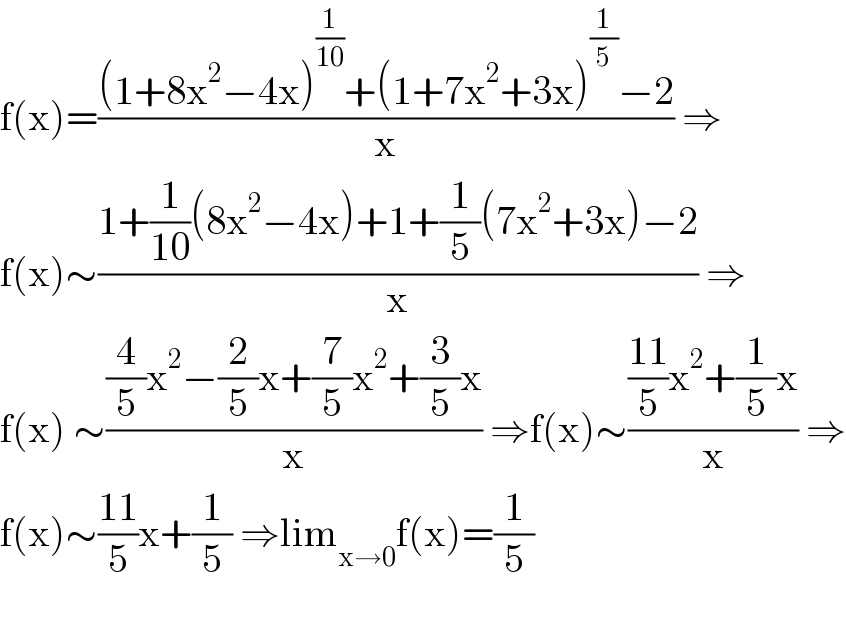 | ||
| ||