Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 161463 by ZiYangLee last updated on 18/Dec/21

Let f(x)= x+∣x∣−1. Find lim_(x→0^+ ) ((f(x)−f(0))/(x−0)) and lim_(x→0^− ) ((f(x)−f(0))/(x−0)). Hence, determine whether f(x) is differentiable at x=0.

$$\mathrm{Let}\:{f}\left({x}\right)=\:{x}+\mid{x}\mid−\mathrm{1}.\: \\ $$$$\mathrm{Find}\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{{f}\left({x}\right)−{f}\left(\mathrm{0}\right)}{{x}−\mathrm{0}}\:\mathrm{and}\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{{f}\left({x}\right)−{f}\left(\mathrm{0}\right)}{{x}−\mathrm{0}}. \\ $$$$\mathrm{Hence},\:\mathrm{determine}\:\mathrm{whether}\:{f}\left({x}\right)\:\mathrm{is}\: \\ $$$$\mathrm{differentiable}\:\mathrm{at}\:{x}=\mathrm{0}. \\ $$

Answered by TheSupreme last updated on 18/Dec/21

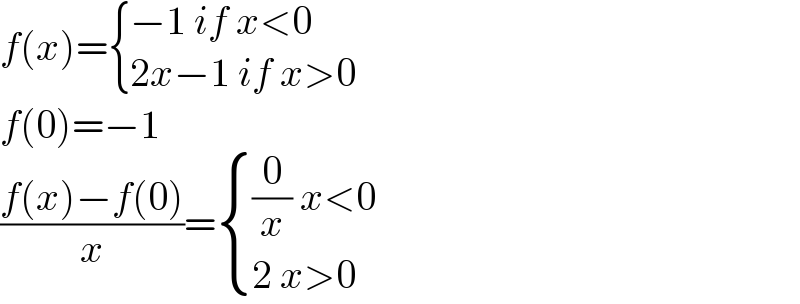
f(x)= { ((−1 if x<0)),((2x−1 if x>0)) :} f(0)=−1 ((f(x)−f(0))/x)= { (((0/x) x<0)),((2 x>0)) :}

$${f}\left({x}\right)=\begin{cases}{−\mathrm{1}\:{if}\:{x}<\mathrm{0}}\\{\mathrm{2}{x}−\mathrm{1}\:{if}\:{x}>\mathrm{0}}\end{cases} \\ $$$${f}\left(\mathrm{0}\right)=−\mathrm{1} \\ $$$$\frac{{f}\left({x}\right)−{f}\left(\mathrm{0}\right)}{{x}}=\begin{cases}{\frac{\mathrm{0}}{{x}}\:{x}<\mathrm{0}}\\{\mathrm{2}\:{x}>\mathrm{0}}\end{cases} \\ $$

Answered by mathmax by abdo last updated on 18/Dec/21

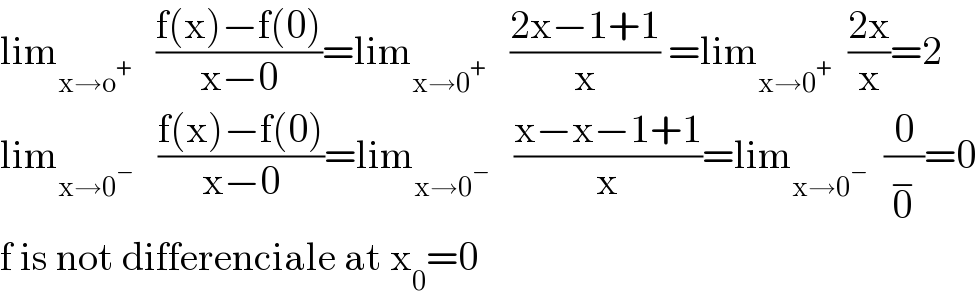
lim_(x→o^+ ) ((f(x)−f(0))/(x−0))=lim_(x→0^+ ) ((2x−1+1)/x) =lim_(x→0^+ ) ((2x)/x)=2 lim_(x→0^− ) ((f(x)−f(0))/(x−0))=lim_(x→0^− ) ((x−x−1+1)/x)=lim_(x→0^− ) (0/0^− )=0 f is not differenciale at x_0 =0

$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{o}^{+} } \:\:\:\frac{\mathrm{f}\left(\mathrm{x}\right)−\mathrm{f}\left(\mathrm{0}\right)}{\mathrm{x}−\mathrm{0}}=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\:\frac{\mathrm{2x}−\mathrm{1}+\mathrm{1}}{\mathrm{x}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\frac{\mathrm{2x}}{\mathrm{x}}=\mathrm{2} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{−} } \:\:\:\frac{\mathrm{f}\left(\mathrm{x}\right)−\mathrm{f}\left(\mathrm{0}\right)}{\mathrm{x}−\mathrm{0}}=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{−} } \:\:\:\frac{\mathrm{x}−\mathrm{x}−\mathrm{1}+\mathrm{1}}{\mathrm{x}}=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{−} } \:\:\frac{\mathrm{0}}{\overset{−} {\mathrm{0}}}=\mathrm{0} \\ $$$$\mathrm{f}\:\mathrm{is}\:\mathrm{not}\:\mathrm{differenciale}\:\mathrm{at}\:\mathrm{x}_{\mathrm{0}} =\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com