Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 161500 by HongKing last updated on 18/Dec/21

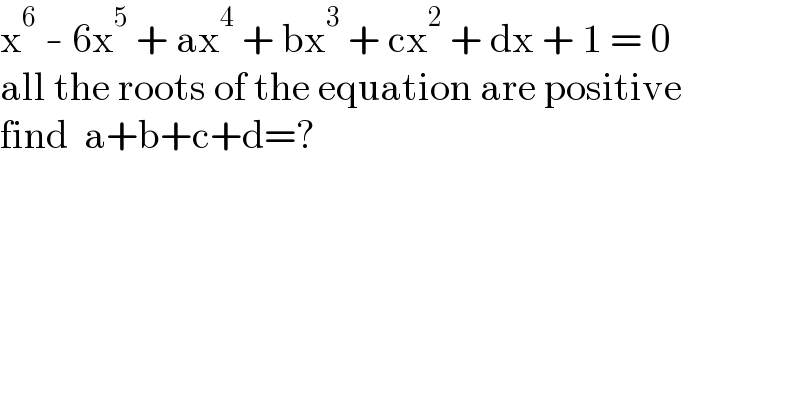
x^6 - 6x^5 + ax^4 + bx^3 + cx^2 + dx + 1 = 0 all the roots of the equation are positive find a+b+c+d=?

$$\mathrm{x}^{\mathrm{6}} \:-\:\mathrm{6x}^{\mathrm{5}} \:+\:\mathrm{ax}^{\mathrm{4}} \:+\:\mathrm{bx}^{\mathrm{3}} \:+\:\mathrm{cx}^{\mathrm{2}} \:+\:\mathrm{dx}\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{all}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{are}\:\mathrm{positive} \\ $$$$\mathrm{find}\:\:\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}=? \\ $$

Answered by mr W last updated on 19/Dec/21

f(x)=x^6 -6x^5 +ax^4 +bx^3 +cx^2 +dx+1=0 it has six roots, say x_1 ,x_2 ,x_3 ,...,x_6 . given: x_1 ,x_2 ,x_3 ,...,x_6 > 0 we have x_1 +x_2 +x_3 +...+x_6 =−(−6)=6 x_1 x_2 x_3 ...x_6 =1 ⇒the only possibility is x_1 =x_2 =x_3 =...=x_6 =1 ⇒f(x)=k(x−1)^6 with k=1, i.e. f(x)=x^6 -6x^5 +ax^4 +bx^3 +cx^2 +dx+1=(x−1)^6 with x=1: f(1)=1-6+a+b+c+d+1=(1−1)^6 =0 ⇒a+b+c+d=4 or (x−1)^6 =x^6 −6x^5 +15x^4 −20x^3 +15x^2 −6x+1 ⇒a=15, b=−20, c=15, d=−6 ⇒a+b+c+d=15−20+15−6=4

$${f}\left({x}\right)=\mathrm{x}^{\mathrm{6}} -\mathrm{6x}^{\mathrm{5}} +\mathrm{ax}^{\mathrm{4}} +\mathrm{bx}^{\mathrm{3}} +\mathrm{cx}^{\mathrm{2}} +\mathrm{dx}+\mathrm{1}=\mathrm{0} \\ $$$${it}\:{has}\:{six}\:{roots},\:{say}\:{x}_{\mathrm{1}} ,{x}_{\mathrm{2}} ,{x}_{\mathrm{3}} ,...,{x}_{\mathrm{6}} . \\ $$$${given}:\:{x}_{\mathrm{1}} ,{x}_{\mathrm{2}} ,{x}_{\mathrm{3}} ,...,{x}_{\mathrm{6}} \:>\:\mathrm{0} \\ $$$${we}\:{have}\: \\ $$$$\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +...+{x}_{\mathrm{6}} =−\left(−\mathrm{6}\right)=\mathrm{6} \\ $$$$\:{x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} ...{x}_{\mathrm{6}} =\mathrm{1} \\ $$$$\Rightarrow{the}\:{only}\:{possibility}\:{is}\:\: \\ $$$${x}_{\mathrm{1}} ={x}_{\mathrm{2}} ={x}_{\mathrm{3}} =...={x}_{\mathrm{6}} =\mathrm{1} \\ $$$$\Rightarrow{f}\left({x}\right)={k}\left({x}−\mathrm{1}\right)^{\mathrm{6}} \:{with}\:{k}=\mathrm{1},\:{i}.{e}. \\ $$$${f}\left({x}\right)=\mathrm{x}^{\mathrm{6}} -\mathrm{6x}^{\mathrm{5}} +\mathrm{ax}^{\mathrm{4}} +\mathrm{bx}^{\mathrm{3}} +\mathrm{cx}^{\mathrm{2}} +\mathrm{dx}+\mathrm{1}=\left({x}−\mathrm{1}\right)^{\mathrm{6}} \\ $$$${with}\:{x}=\mathrm{1}: \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}-\mathrm{6}+\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}+\mathrm{1}=\left(\mathrm{1}−\mathrm{1}\right)^{\mathrm{6}} =\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}+\boldsymbol{{d}}=\mathrm{4} \\ $$$$ \\ $$$${or} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{6}} ={x}^{\mathrm{6}} −\mathrm{6}{x}^{\mathrm{5}} +\mathrm{15}{x}^{\mathrm{4}} −\mathrm{20}{x}^{\mathrm{3}} +\mathrm{15}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{1} \\ $$$$\Rightarrow{a}=\mathrm{15},\:{b}=−\mathrm{20},\:{c}=\mathrm{15},\:{d}=−\mathrm{6} \\ $$$$\Rightarrow{a}+{b}+{c}+{d}=\mathrm{15}−\mathrm{20}+\mathrm{15}−\mathrm{6}=\mathrm{4} \\ $$

Commented by Tawa11 last updated on 19/Dec/21

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Commented by HongKing last updated on 19/Dec/21

cool my dear Sir thank you so much

$$\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com