Question Number 161537 by cortano last updated on 19/Dec/21
$$\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} \left({x}\right)}{\mathrm{cot}\:^{\mathrm{2}} \left({x}\right)}\:{dx}\:=? \\ $$
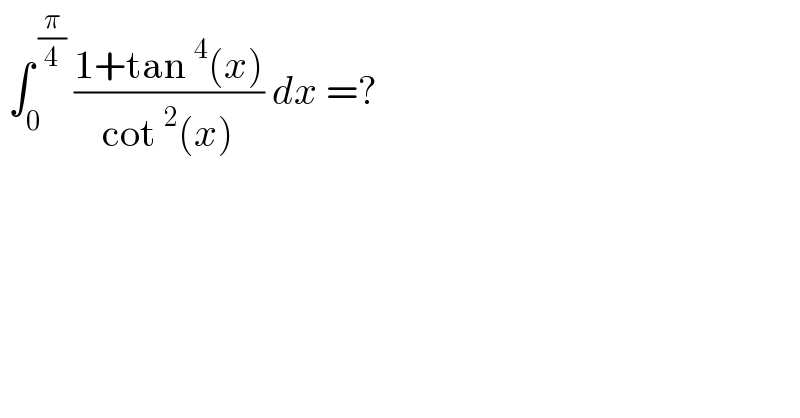
Answered by Ar Brandon last updated on 19/Dec/21
![=∫_0 ^(π/4) (tan^2 x+tan^6 x)dx =∫_0 ^(π/4) (sec^2 x−1)dx+∫_0 ^(π/4) (tan^4 x)(sec^2 x−1)dx =[tanx−x]_0 ^(π/4) +[((tan^5 x)/5)]_0 ^(π/4) −∫_0 ^(π/4) (tan^2 x)(sec^2 x−1)dx =1−(π/4)+(1/5)−[((tan^3 x)/3)]_0 ^(π/4) +∫_0 ^(π/4) (sec^2 x−1)dx =(6/5)−(π/4)−(1/3)+[tanx−x]_0 ^(π/4) =((13)/(15))−(π/4)+(1−(π/4)) =((28)/(15))−(π/2)](Q161549.png)
$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{tan}^{\mathrm{2}} {x}+\mathrm{tan}^{\mathrm{6}} {x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{sec}^{\mathrm{2}} {x}−\mathrm{1}\right){dx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{tan}^{\mathrm{4}} {x}\right)\left(\mathrm{sec}^{\mathrm{2}} {x}−\mathrm{1}\right){dx} \\ $$$$=\left[\mathrm{tan}{x}−{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} +\left[\frac{\mathrm{tan}^{\mathrm{5}} {x}}{\mathrm{5}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} −\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{tan}^{\mathrm{2}} {x}\right)\left(\mathrm{sec}^{\mathrm{2}} {x}−\mathrm{1}\right){dx} \\ $$$$=\mathrm{1}−\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}−\left[\frac{\mathrm{tan}^{\mathrm{3}} {x}}{\mathrm{3}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} +\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{sec}^{\mathrm{2}} {x}−\mathrm{1}\right){dx} \\ $$$$=\frac{\mathrm{6}}{\mathrm{5}}−\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{3}}+\left[\mathrm{tan}{x}−{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\frac{\mathrm{13}}{\mathrm{15}}−\frac{\pi}{\mathrm{4}}+\left(\mathrm{1}−\frac{\pi}{\mathrm{4}}\right) \\ $$$$=\frac{\mathrm{28}}{\mathrm{15}}−\frac{\pi}{\mathrm{2}} \\ $$
Commented by Ar Brandon last updated on 19/Dec/21
$$\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}=\mathrm{sec}^{\mathrm{2}} {x} \\ $$$$\frac{{d}\left(\mathrm{tan}{x}\right)}{{dx}}=\mathrm{sec}^{\mathrm{2}} {x} \\ $$
Commented by peter frank last updated on 20/Dec/21
$$\mathrm{good} \\ $$
Answered by cortano last updated on 19/Dec/21
Commented by saboorhalimi last updated on 19/Dec/21
$${sir}\:{which}\:{software}\:{did}\:{you}\:{use}\: \\ $$$${for}\:{writing}\:{this}\:{solution}? \\ $$
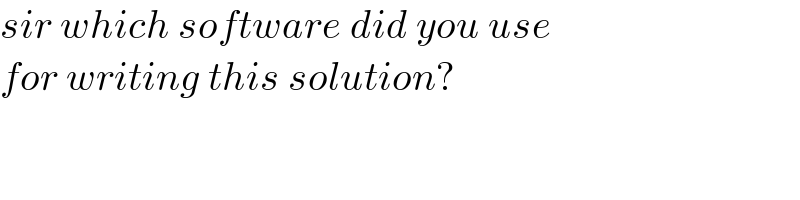
Commented by cortano last updated on 20/Dec/21
$${math}\:{editor}\:{for}\:{pc} \\ $$