Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 161706 by mnjuly1970 last updated on 21/Dec/21

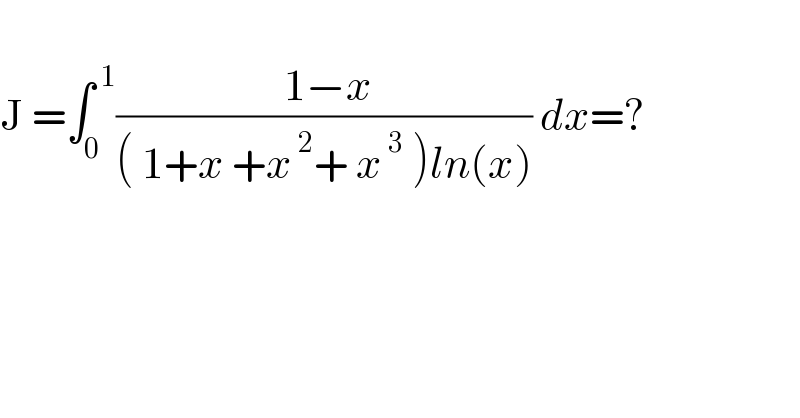
J =∫_0 ^( 1) (( 1−x)/(( 1+x +x^( 2) + x^( 3) )ln(x))) dx=?

$$\: \\ $$$$\mathrm{J}\:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\mathrm{1}−{x}}{\left(\:\mathrm{1}+{x}\:+{x}^{\:\mathrm{2}} +\:{x}^{\:\mathrm{3}} \:\right){ln}\left({x}\right)}\:{dx}=? \\ $$$$ \\ $$

Answered by Ar Brandon last updated on 21/Dec/21

f(α)=∫_0 ^1 ((1−x^α )/((1+x+x^2 +x^3 )lnx))dx⇒f(1)=∫_0 ^1 ((1−x)/((1+x+x^2 +x^3 )lnx))dx f ′(α)=−∫_0 ^1 (x^α /(1+x+x^2 +x^3 ))dx=−∫_0 ^1 ((x^α (1−x))/(1−x^4 ))dx =∫_0 ^1 ((x^(α+1) −x^α )/(1−x^4 ))dx=(1/4)∫_0 ^1 ((x^((α/4)−(1/2)) −x^((α/4)−(3/4)) )/(1−x))dx =(1/4)(ψ((α/4)+(1/4))−ψ((α/4)+(1/2))) ⇒f(α)=ln(Γ((α/4)+(1/4)))−ln(Γ((α/4)+(1/2)))+C f(0)=0=ln(Γ((1/4)))−ln(Γ((1/2)))+C ⇒f(α)=ln(Γ((α/4)+(1/4)))−ln(Γ((α/4)+(1/2)))+ln(Γ((1/2)))−ln(Γ((1/4))) ⇒f(1)=ln(Γ((1/2)))−ln(Γ((3/4)))+ln(Γ((1/2)))−ln(Γ((1/4))) =ln(Γ^2 ((1/2)))−ln(Γ((1/4))Γ((3/4)))=lnπ−ln((π/(sin((π/4))))) =lnπ−ln(π(√2))=ln((π/(π(√2))))=−((ln2)/2)

$${f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{\alpha} }{\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right)\mathrm{ln}{x}}{dx}\Rightarrow{f}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}}{\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right)\mathrm{ln}{x}}{dx} \\ $$$${f}\:'\left(\alpha\right)=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\alpha} }{\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\alpha} \left(\mathrm{1}−{x}\right)}{\mathrm{1}−{x}^{\mathrm{4}} }{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\alpha+\mathrm{1}} −{x}^{\alpha} }{\mathrm{1}−{x}^{\mathrm{4}} }{dx}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\frac{\alpha}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}} −{x}^{\frac{\alpha}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{4}}} }{\mathrm{1}−{x}}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left(\psi\left(\frac{\alpha}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\right)−\psi\left(\frac{\alpha}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$\Rightarrow{f}\left(\alpha\right)=\mathrm{ln}\left(\Gamma\left(\frac{\alpha}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\right)−\mathrm{ln}\left(\Gamma\left(\frac{\alpha}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+{C} \\ $$$$\:\:\:\:\:{f}\left(\mathrm{0}\right)=\mathrm{0}=\mathrm{ln}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right)−\mathrm{ln}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+{C} \\ $$$$\Rightarrow{f}\left(\alpha\right)=\mathrm{ln}\left(\Gamma\left(\frac{\alpha}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\right)−\mathrm{ln}\left(\Gamma\left(\frac{\alpha}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+\mathrm{ln}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)−\mathrm{ln}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right) \\ $$$$\Rightarrow{f}\left(\mathrm{1}\right)=\mathrm{ln}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)−\mathrm{ln}\left(\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right)+\mathrm{ln}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)−\mathrm{ln}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{ln}\left(\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)−\mathrm{ln}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right)=\mathrm{ln}\pi−\mathrm{ln}\left(\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{ln}\pi−\mathrm{ln}\left(\pi\sqrt{\mathrm{2}}\right)=\mathrm{ln}\left(\frac{\pi}{\pi\sqrt{\mathrm{2}}}\right)=−\frac{\mathrm{ln2}}{\mathrm{2}} \\ $$

Commented by mnjuly1970 last updated on 21/Dec/21

very nice solution mr brandon thank you so much

$$\:\:\:\:\:{very}\:{nice}\:{solution}\:{mr}\:{brandon} \\ $$$${thank}\:{you}\:{so}\:{much} \\ $$

Commented by Ar Brandon last updated on 21/Dec/21

You're welcome Sir.

Terms of Service

Privacy Policy

Contact: info@tinkutara.com