
Question and Answers Forum
Question Number 161723 by LEKOUMA last updated on 21/Dec/21
![Calculate lim_(x→0) (((1+x.2^x )/(1+x.3^x )))^(1/x^2 ) lim_(x→0) [2e^(x/(x+1)) −1]^((x^2 +1)/x) lim_(x→a) ((x^x −a^a )/(x−a))](Q161723.png)
Answered by cortano last updated on 21/Dec/21
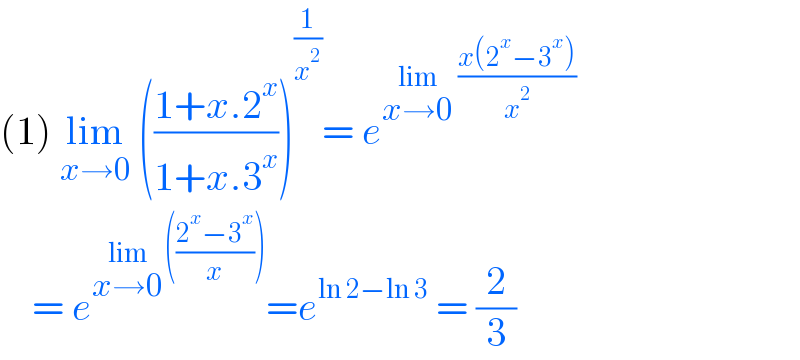
Answered by cortano last updated on 21/Dec/21
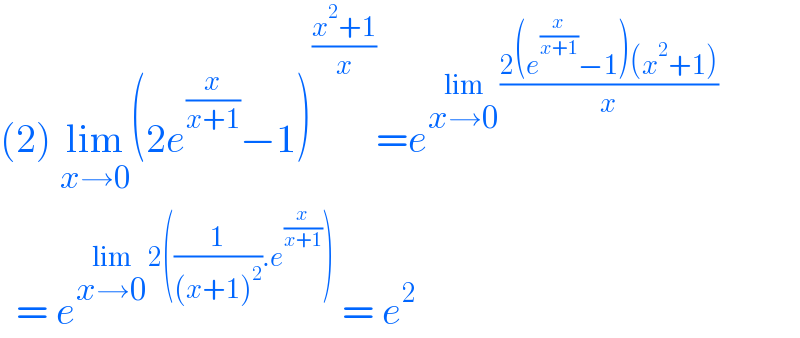
Commented by LEKOUMA last updated on 21/Dec/21

Answered by Ar Brandon last updated on 21/Dec/21
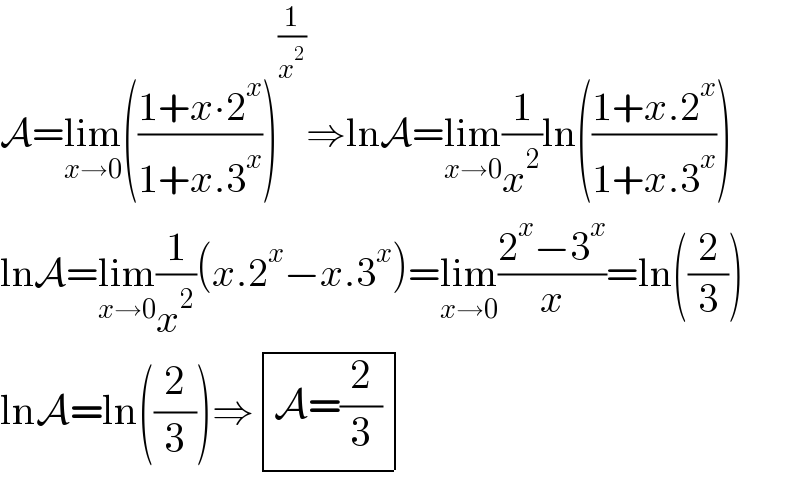
Answered by Ar Brandon last updated on 21/Dec/21
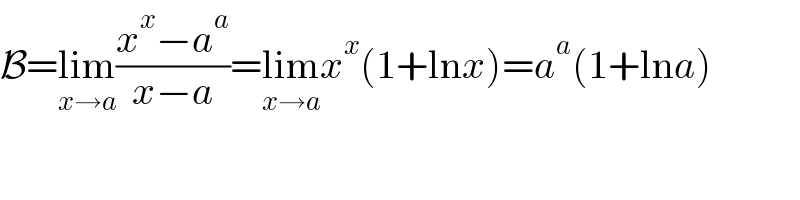
Commented by LEKOUMA last updated on 21/Dec/21

