
Question and Answers Forum
Question Number 161745 by HongKing last updated on 21/Dec/21
![Prove that: 3 (√e) = (1/3) Σ_(k=1) ^∞ [ Σ_(n=0) ^∞ (1/(n!)) ]k2^(-k)](Q161745.png)
Commented by mr W last updated on 22/Dec/21
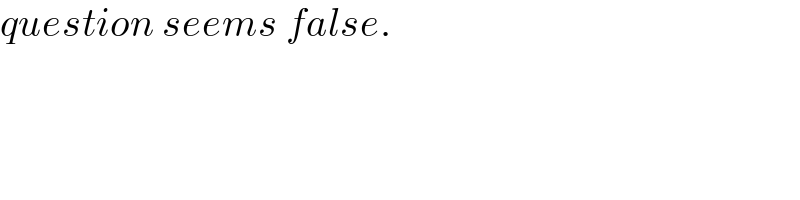
Answered by mr W last updated on 22/Dec/21
![Σ_(k=1) ^∞ x^k =(x/(1−x)) for ∣x∣<1 Σ_(k=1) ^∞ kx^(k−1) =(1/(1−x))+(x/((1−x)^2 )) Σ_(k=1) ^∞ kx^k =(x/(1−x))+(x^2 /((1−x)^2 )) with x=(1/2) ⇒Σ_(k=1) ^∞ k2^(−k) =((1/2)/(1−(1/2)))+((((1/2))^2 )/((1−(1/2))^2 ))=2 e^x =Σ_(n=0) ^∞ (x^n /(n!)) with x=1 ⇒Σ_(n=0) ^∞ (1/(n!))=e (1/3) Σ_(k=1) ^∞ [ Σ_(n=0) ^∞ (1/(n!)) ]k2^(-k) =(1/3) Σ_(k=1) ^∞ (e) k2^(-k) =(e/3) Σ_(k=1) ^∞ k2^(-k) =(e/3)×2 =((2e)/3)≠3(√e)](Q161756.png)
Commented by HongKing last updated on 22/Dec/21
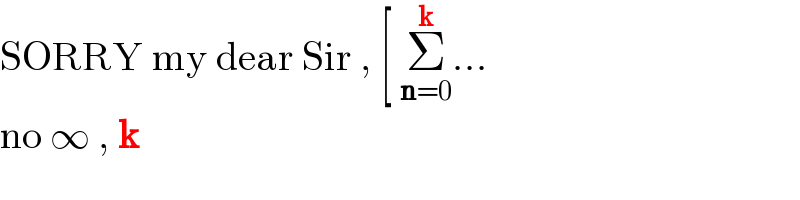
| ||
Question and Answers Forum | ||
Question Number 161745 by HongKing last updated on 21/Dec/21 | ||
![Prove that: 3 (√e) = (1/3) Σ_(k=1) ^∞ [ Σ_(n=0) ^∞ (1/(n!)) ]k2^(-k)](Q161745.png) | ||
Commented by mr W last updated on 22/Dec/21 | ||
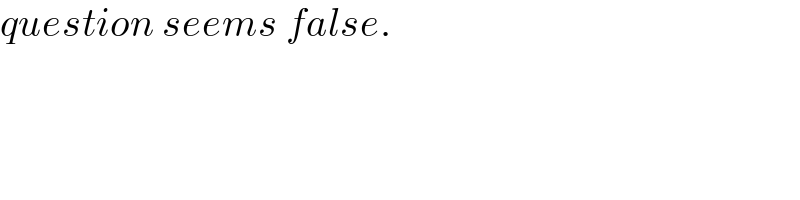 | ||
Answered by mr W last updated on 22/Dec/21 | ||
![Σ_(k=1) ^∞ x^k =(x/(1−x)) for ∣x∣<1 Σ_(k=1) ^∞ kx^(k−1) =(1/(1−x))+(x/((1−x)^2 )) Σ_(k=1) ^∞ kx^k =(x/(1−x))+(x^2 /((1−x)^2 )) with x=(1/2) ⇒Σ_(k=1) ^∞ k2^(−k) =((1/2)/(1−(1/2)))+((((1/2))^2 )/((1−(1/2))^2 ))=2 e^x =Σ_(n=0) ^∞ (x^n /(n!)) with x=1 ⇒Σ_(n=0) ^∞ (1/(n!))=e (1/3) Σ_(k=1) ^∞ [ Σ_(n=0) ^∞ (1/(n!)) ]k2^(-k) =(1/3) Σ_(k=1) ^∞ (e) k2^(-k) =(e/3) Σ_(k=1) ^∞ k2^(-k) =(e/3)×2 =((2e)/3)≠3(√e)](Q161756.png) | ||
| ||
Commented by HongKing last updated on 22/Dec/21 | ||
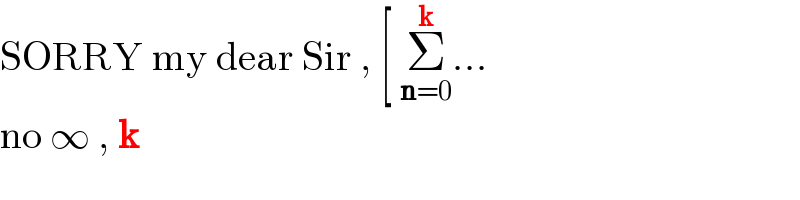 | ||