
Question and Answers Forum
Question Number 161755 by mkam last updated on 22/Dec/21
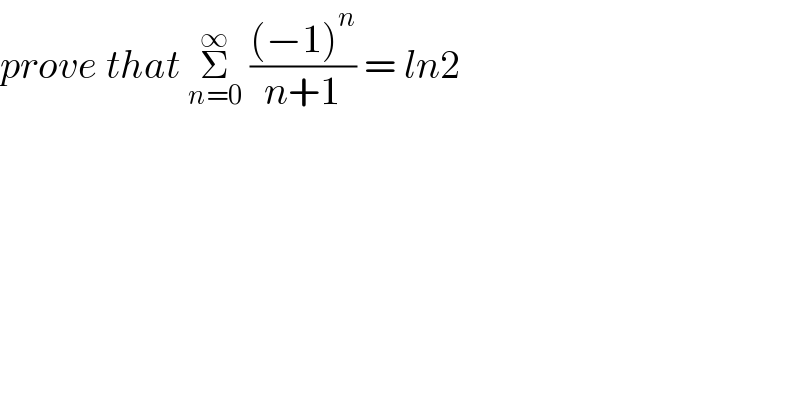
Answered by FelipeLz last updated on 22/Dec/21

Answered by Ar Brandon last updated on 22/Dec/21
![S=Σ_(n=0) ^∞ (((−1)^n )/(n+1))=Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^n dx =Σ_(n=0) ^∞ ∫_0 ^1 (−x)^n dx=∫_0 ^1 Σ_(n=0) ^∞ (−x)^n dx =∫_0 ^1 (1/(1+x))dx=[ln(1+x)]_0 ^1 =ln(2)−ln(1) ⇒ determinant (((Σ_(n=0) ^∞ (((−1)^n )/(n+1))=ln(2))))](Q161774.png)
| ||
Question and Answers Forum | ||
Question Number 161755 by mkam last updated on 22/Dec/21 | ||
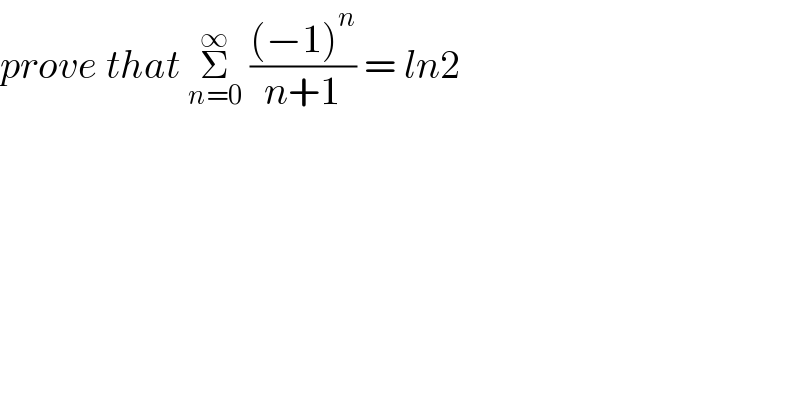 | ||
Answered by FelipeLz last updated on 22/Dec/21 | ||
 | ||
| ||
Answered by Ar Brandon last updated on 22/Dec/21 | ||
![S=Σ_(n=0) ^∞ (((−1)^n )/(n+1))=Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^n dx =Σ_(n=0) ^∞ ∫_0 ^1 (−x)^n dx=∫_0 ^1 Σ_(n=0) ^∞ (−x)^n dx =∫_0 ^1 (1/(1+x))dx=[ln(1+x)]_0 ^1 =ln(2)−ln(1) ⇒ determinant (((Σ_(n=0) ^∞ (((−1)^n )/(n+1))=ln(2))))](Q161774.png) | ||
| ||