
Question Number 161773 by smallEinstein last updated on 22/Dec/21

Commented by Tawa11 last updated on 22/Dec/21
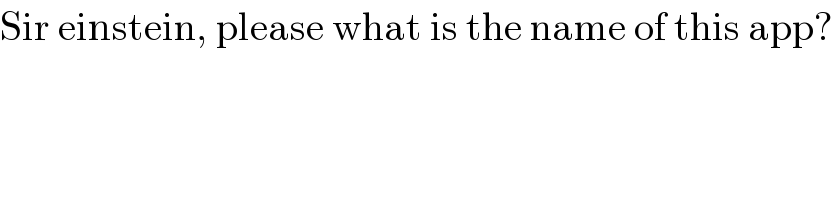
$$\mathrm{Sir}\:\mathrm{einstein},\:\mathrm{please}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{name}\:\mathrm{of}\:\mathrm{this}\:\mathrm{app}? \\ $$
Answered by Ar Brandon last updated on 22/Dec/21
![I=∫_0 ^∞ x^2 e^(−2x) sin(2x)lnxdx=(∂/∂α)∣_(α=2) ∫_0 ^∞ x^α e^(−2x) sin(2x)dx =(∂/∂α)∣_(α=2) (1/2^(α+1) )∫_0 ^∞ t^α e^(−t) sin(t)dt=(∂/∂α)∣_(α=2) (1/2^(α+1) )∫_0 ^∞ t^α e^(−t) (((e^(it) −e^(−it) )/(2i)))dt =(∂/∂α)∣_(α=2) (i/2^(α+2) )∫_0 ^∞ t^α (e^(−(1+i)t) −e^(−(1−i)t) )dt =(∂/∂α)∣_(α=2) (i/2^(α+2) )[∫_0 ^∞ t^α e^(−(1+i)t) dt−∫_0 ^∞ t^α e^(−(1−i)t) dt] =(∂/∂α)∣_(α=2) (i/2^(α+2) )[(1/((1+i)^(α+1) ))∫_0 ^∞ u^α e^(−u) du−(1/((1−i)^(α+1) ))∫_0 ^∞ v^α e^(−v) dv =(∂/∂α)∣_(α=2) (i/2^(α+2) )[((Γ(α+1))/((1+i)^(α+1) ))−((Γ(α+1))/((1−i)^(α+1) ))]=(i/2)∙(∂/∂α)∣_(α=2) [(1/((2+2i)^(α+1) ))−(1/((2−2i)^(α+1) ))]Γ(α+1) =(i/2)∙∣_(α=2) ((1/((2+2i)^(α+1) ))−(1/((2−2i)^(α+1) )))Γ′(α+1)+(((ln(2−2i))/((2−2i)^(α+1) ))−((ln(2+2i))/((2+2i)^(α+1) )))Γ(α+1) =(i/2)[((1/((2+2i)^3 ))−(1/((2−2i)^3 )))Γ′(3)+(((ln(2−2i))/((2−2i)^3 ))−((ln(2+2i))/((2+2i)^3 )))Γ(3) =(i/2)[(((8e^(−(3/4)iπ) −8e^((3/4)iπ) )/(512)))Γ(3)ψ(3)+(((8e^((3/4)iπ) ln2e^(−(π/4)i) −8e^(−(3/4)iπ) ln2e^((π/4)i) )/(512)))Γ(3)] =(i/(64))(−2isin(((3π)/4)))((3/2)−γ)+(i/(64))(e^((3/4)iπ) (ln2−(π/4)i)−e^(−(3/4)iπ) (ln2+(π/4)i)) =((√2)/(64))((3/2)−γ)+(i/(64))((e^((3/4)iπ) −e^(−(3/4)iπ) )ln2−(π/4)(e^((5/4)iπ) +e^(−(1/4)iπ) )) =((√2)/(64))((3/2)−γ)−(1/(32))sin(((3π)/4))ln2+(π/(256))i(2isin((π/4))) =((√2)/(64))((3/2)−γ)−((√2)/(64))ln2−((π(√2))/(256))=−(π/( 128(√2)))−(1/(32(√2)))γ−(1/(32(√2)))ln2+(3/( 64(√2))) Still checking for typos](Q161780.png)
$${I}=\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {e}^{−\mathrm{2}{x}} \mathrm{sin}\left(\mathrm{2}{x}\right)\mathrm{ln}{xdx}=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \int_{\mathrm{0}} ^{\infty} {x}^{\alpha} {e}^{−\mathrm{2}{x}} \mathrm{sin}\left(\mathrm{2}{x}\right){dx} \\ $$$$\:\:\:=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}^{\alpha+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} {t}^{\alpha} {e}^{−{t}} \mathrm{sin}\left({t}\right){dt}=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}^{\alpha+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} {t}^{\alpha} {e}^{−{t}} \left(\frac{{e}^{{it}} −{e}^{−{it}} }{\mathrm{2}{i}}\right){dt} \\ $$$$\:\:\:=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \frac{{i}}{\mathrm{2}^{\alpha+\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} {t}^{\alpha} \left({e}^{−\left(\mathrm{1}+{i}\right){t}} −{e}^{−\left(\mathrm{1}−{i}\right){t}} \right){dt} \\ $$$$\:\:\:=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \frac{{i}}{\mathrm{2}^{\alpha+\mathrm{2}} }\left[\int_{\mathrm{0}} ^{\infty} {t}^{\alpha} {e}^{−\left(\mathrm{1}+{i}\right){t}} {dt}−\int_{\mathrm{0}} ^{\infty} {t}^{\alpha} {e}^{−\left(\mathrm{1}−{i}\right){t}} {dt}\right] \\ $$$$\:\:\:=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \frac{{i}}{\mathrm{2}^{\alpha+\mathrm{2}} }\left[\frac{\mathrm{1}}{\left(\mathrm{1}+{i}\right)^{\alpha+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} {u}^{\alpha} {e}^{−{u}} {du}−\frac{\mathrm{1}}{\left(\mathrm{1}−{i}\right)^{\alpha+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} {v}^{\alpha} {e}^{−{v}} {dv}\right. \\ $$$$\:\:\:=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \frac{{i}}{\mathrm{2}^{\alpha+\mathrm{2}} }\left[\frac{\Gamma\left(\alpha+\mathrm{1}\right)}{\left(\mathrm{1}+{i}\right)^{\alpha+\mathrm{1}} }−\frac{\Gamma\left(\alpha+\mathrm{1}\right)}{\left(\mathrm{1}−{i}\right)^{\alpha+\mathrm{1}} }\right]=\frac{{i}}{\mathrm{2}}\centerdot\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \left[\frac{\mathrm{1}}{\left(\mathrm{2}+\mathrm{2}{i}\right)^{\alpha+\mathrm{1}} }−\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{2}{i}\right)^{\alpha+\mathrm{1}} }\right]\Gamma\left(\alpha+\mathrm{1}\right) \\ $$$$\:\:\:=\frac{{i}}{\mathrm{2}}\centerdot\mid_{\alpha=\mathrm{2}} \left(\frac{\mathrm{1}}{\left(\mathrm{2}+\mathrm{2}{i}\right)^{\alpha+\mathrm{1}} }−\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{2}{i}\right)^{\alpha+\mathrm{1}} }\right)\Gamma'\left(\alpha+\mathrm{1}\right)+\left(\frac{\mathrm{ln}\left(\mathrm{2}−\mathrm{2}{i}\right)}{\left(\mathrm{2}−\mathrm{2}{i}\right)^{\alpha+\mathrm{1}} }−\frac{\mathrm{ln}\left(\mathrm{2}+\mathrm{2}{i}\right)}{\left(\mathrm{2}+\mathrm{2}{i}\right)^{\alpha+\mathrm{1}} }\right)\Gamma\left(\alpha+\mathrm{1}\right) \\ $$$$\:\:\:=\frac{{i}}{\mathrm{2}}\left[\left(\frac{\mathrm{1}}{\left(\mathrm{2}+\mathrm{2}{i}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{2}{i}\right)^{\mathrm{3}} }\right)\Gamma'\left(\mathrm{3}\right)+\left(\frac{\mathrm{ln}\left(\mathrm{2}−\mathrm{2}{i}\right)}{\left(\mathrm{2}−\mathrm{2}{i}\right)^{\mathrm{3}} }−\frac{\mathrm{ln}\left(\mathrm{2}+\mathrm{2}{i}\right)}{\left(\mathrm{2}+\mathrm{2}{i}\right)^{\mathrm{3}} }\right)\Gamma\left(\mathrm{3}\right)\right. \\ $$$$\:\:\:=\frac{{i}}{\mathrm{2}}\left[\left(\frac{\mathrm{8}{e}^{−\frac{\mathrm{3}}{\mathrm{4}}{i}\pi} −\mathrm{8}{e}^{\frac{\mathrm{3}}{\mathrm{4}}{i}\pi} }{\mathrm{512}}\right)\Gamma\left(\mathrm{3}\right)\psi\left(\mathrm{3}\right)+\left(\frac{\mathrm{8}{e}^{\frac{\mathrm{3}}{\mathrm{4}}{i}\pi} \mathrm{ln2}{e}^{−\frac{\pi}{\mathrm{4}}{i}} −\mathrm{8}{e}^{−\frac{\mathrm{3}}{\mathrm{4}}{i}\pi} \mathrm{ln2}{e}^{\frac{\pi}{\mathrm{4}}{i}} }{\mathrm{512}}\right)\Gamma\left(\mathrm{3}\right)\right] \\ $$$$\:\:\:=\frac{{i}}{\mathrm{64}}\left(−\mathrm{2}{i}\mathrm{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)\right)\left(\frac{\mathrm{3}}{\mathrm{2}}−\gamma\right)+\frac{{i}}{\mathrm{64}}\left({e}^{\frac{\mathrm{3}}{\mathrm{4}}{i}\pi} \left(\mathrm{ln2}−\frac{\pi}{\mathrm{4}}{i}\right)−{e}^{−\frac{\mathrm{3}}{\mathrm{4}}{i}\pi} \left(\mathrm{ln2}+\frac{\pi}{\mathrm{4}}{i}\right)\right) \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{64}}\left(\frac{\mathrm{3}}{\mathrm{2}}−\gamma\right)+\frac{{i}}{\mathrm{64}}\left(\left({e}^{\frac{\mathrm{3}}{\mathrm{4}}{i}\pi} −{e}^{−\frac{\mathrm{3}}{\mathrm{4}}{i}\pi} \right)\mathrm{ln2}−\frac{\pi}{\mathrm{4}}\left({e}^{\frac{\mathrm{5}}{\mathrm{4}}{i}\pi} +{e}^{−\frac{\mathrm{1}}{\mathrm{4}}{i}\pi} \right)\right) \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{64}}\left(\frac{\mathrm{3}}{\mathrm{2}}−\gamma\right)−\frac{\mathrm{1}}{\mathrm{32}}\mathrm{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)\mathrm{ln2}+\frac{\pi}{\mathrm{256}}{i}\left(\mathrm{2}{i}\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)\right) \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{64}}\left(\frac{\mathrm{3}}{\mathrm{2}}−\gamma\right)−\frac{\sqrt{\mathrm{2}}}{\mathrm{64}}\mathrm{ln2}−\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{256}}=−\frac{\pi}{\:\mathrm{128}\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{32}\sqrt{\mathrm{2}}}\gamma−\frac{\mathrm{1}}{\mathrm{32}\sqrt{\mathrm{2}}}\mathrm{ln2}+\frac{\mathrm{3}}{\:\mathrm{64}\sqrt{\mathrm{2}}} \\ $$$${Still}\:{checking}\:{for}\:{typos} \\ $$
Answered by Lordose last updated on 22/Dec/21

$$ \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{2x}} \mathrm{sin}\left(\mathrm{2x}\right)\mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{I}\:=\:\frac{\partial}{\partial\mathrm{a}}\mid_{\mathrm{a}=\mathrm{2}} \int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{a}} \mathrm{e}^{−\mathrm{2x}} \mathrm{sin}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$\mathrm{I}\:\overset{\mathrm{x}=\frac{\mathrm{x}}{\mathrm{2}}} {=}\frac{\partial}{\partial\mathrm{a}}\mid_{\mathrm{a}=\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}^{\mathrm{a}+\mathrm{1}} }\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{a}} \mathrm{e}^{−\mathrm{x}} \mathrm{sin}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{I}\:=\:\boldsymbol{\mathfrak{Im}}\frac{\partial}{\partial\mathrm{a}}\mid_{\mathrm{a}=\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}^{\mathrm{a}+\mathrm{1}} }\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{a}} \mathrm{e}^{−\mathrm{x}\left(\mathrm{1}−\boldsymbol{\mathrm{i}}\right)} \mathrm{dx} \\ $$$$\mathrm{I}\:\overset{\mathrm{x}=\mathrm{x}\left(\mathrm{1}−\boldsymbol{\mathrm{i}}\right)} {=}\:\boldsymbol{\mathfrak{Im}}\frac{\partial}{\partial\mathrm{a}}\mid_{\mathrm{a}=\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}^{\mathrm{a}+\mathrm{1}} \left(\mathrm{1}−\mathrm{i}\right)^{\mathrm{a}+\mathrm{1}} }\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{a}+\mathrm{1}−\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{dx} \\ $$$$\mathrm{I}\:=\:\boldsymbol{\mathfrak{Im}}\frac{\partial}{\partial\mathrm{a}}\mid_{\mathrm{a}=\mathrm{2}} \frac{\boldsymbol{\Gamma}\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{2}^{\mathrm{a}+\mathrm{1}} \left(\mathrm{1}−\mathrm{i}\right)^{\mathrm{a}+\mathrm{1}} } \\ $$$$\mathrm{I}\:=\:\boldsymbol{\mathfrak{Im}}\mid\frac{\boldsymbol{\psi}\left(\mathrm{a}+\mathrm{1}\right)\boldsymbol{\Gamma}\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{2}^{\mathrm{a}+\mathrm{1}} \left(\mathrm{1}−\boldsymbol{\mathrm{i}}\right)^{\mathrm{a}+\mathrm{1}} }\:−\:\frac{\boldsymbol{\Gamma}\left(\mathrm{a}+\mathrm{1}\right)\mathrm{ln}\left(\mathrm{2}\right)+\boldsymbol{\Gamma}\left(\mathrm{a}+\mathrm{1}\right)\mathrm{ln}\left(\mathrm{1}−\mathrm{i}\right)}{\mathrm{2}^{\mathrm{a}+\mathrm{1}} \left(\mathrm{1}−\boldsymbol{\mathrm{i}}\right)^{\mathrm{a}+\mathrm{1}} }\mid_{\mathrm{a}=\mathrm{2}} \\ $$$$\mathrm{I}\:=\:\boldsymbol{\mathfrak{Im}}\left(\frac{\boldsymbol{\psi}\left(\mathrm{3}\right)\boldsymbol{\Gamma}\left(\mathrm{3}\right)}{\mathrm{2}^{\mathrm{3}} \left(\mathrm{1}−\boldsymbol{\mathrm{i}}\right)^{\mathrm{3}} }\:−\:\frac{\boldsymbol{\Gamma}\left(\mathrm{3}\right)\mathrm{ln}\left(\mathrm{2}\right)+\boldsymbol{\Gamma}\left(\mathrm{3}\right)\mathrm{ln}\left(\mathrm{1}−\boldsymbol{\mathrm{i}}\right)}{\mathrm{2}^{\mathrm{3}} \left(\mathrm{1}−\boldsymbol{\mathrm{i}}\right)^{\mathrm{3}} }\right) \\ $$$$\mathrm{I}\:=\:\boldsymbol{\mathfrak{Im}}\left(\frac{\mathrm{1}}{\mathrm{64}}\left(\mathrm{4}\boldsymbol{\gamma}+\boldsymbol{\pi}−\mathrm{2}\left(\mathrm{3}+\mathrm{ln}\left(\mathrm{8}\right)\right)+\mathrm{i}\left(\mathrm{6}−\mathrm{4}\boldsymbol{\gamma}−\boldsymbol{\pi}−\mathrm{ln}\left(\mathrm{64}\right)\right)\right)\right) \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{64}}\left(\mathrm{6}−\mathrm{4}\boldsymbol{\gamma}\:−\:\boldsymbol{\pi}\:−\:\mathrm{6ln}\left(\mathrm{2}\right)\right) \\ $$
Commented by Ar Brandon last updated on 22/Dec/21

$$\mathrm{Nice} \\ $$
Answered by mathmax by abdo last updated on 23/Dec/21

$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{x}^{\mathrm{a}+\mathrm{2}} \mathrm{e}^{−\mathrm{x}−\mathrm{2}} \mathrm{sin}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{x}^{\mathrm{a}+\mathrm{2}} \mathrm{e}^{−\mathrm{x}−\mathrm{2}+\mathrm{2ix}} \mathrm{dx}\right) \\ $$$$\mathrm{and}\:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{x}^{\mathrm{a}+\mathrm{2}} \mathrm{e}^{−\mathrm{2}+\left(\mathrm{2i}−\mathrm{1}\right)\mathrm{x}} \mathrm{dx}=_{\left(\mathrm{2i}−\mathrm{1}\right)\mathrm{x}=−\mathrm{t}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\left(\frac{−\mathrm{t}}{\mathrm{2i}−\mathrm{1}}\right)^{\mathrm{a}+\mathrm{2}} \mathrm{e}^{−\mathrm{2}−\mathrm{t}} \:\frac{−\mathrm{dt}}{\left(\mathrm{2i}−\mathrm{1}\right)} \\ $$$$=\mathrm{e}^{−\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2i}−\mathrm{1}}\right)^{\mathrm{a}+\mathrm{3}} \left(−\mathrm{1}\right)^{\mathrm{a}+\mathrm{2}} \int_{\mathrm{0}} ^{\infty} \:\:\:\left(\mathrm{t}\right)^{\mathrm{a}+\mathrm{2}} \mathrm{e}^{−\mathrm{t}} \mathrm{dt} \\ $$$$=\frac{\mathrm{e}^{−\mathrm{2}} \left(−\mathrm{1}\right)^{\mathrm{a}} }{\left(\mathrm{2i}−\mathrm{1}\right)^{\mathrm{a}+\mathrm{3}} }×\Gamma\left(\mathrm{a}+\mathrm{3}\right) \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{2}} \left(\:\mathrm{e}^{\mathrm{alogx}} \right)^{'} \:\mathrm{e}^{−\mathrm{x}−\mathrm{2}} \mathrm{sin}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{2}} \mathrm{logx}\:\mathrm{x}^{\mathrm{a}} \:\mathrm{e}^{−\mathrm{x}−\mathrm{2}} \mathrm{sin}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}−\mathrm{2}} \mathrm{sin}\left(\mathrm{2x}\right)\mathrm{logx}\:\mathrm{dx} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{e}^{−\mathrm{2}} }{\left(\mathrm{2i}−\mathrm{1}\right)^{\mathrm{3}} }\left(−\frac{\mathrm{1}}{\mathrm{2i}−\mathrm{1}}\right)^{\mathrm{a}} .\Gamma\left(\mathrm{a}+\mathrm{3}\right) \\ $$$$=\frac{\mathrm{e}^{−\mathrm{2}} }{\left(\sqrt{\mathrm{5}}\mathrm{e}^{−\mathrm{iarctan}\left(\mathrm{2}\right)} \mathrm{3}\right.}\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}\mathrm{e}^{−\mathrm{iarctan2}} }\right)^{\mathrm{a}} .\Gamma\left(\mathrm{a}+\mathrm{3}\right) \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{a}} \:\mathrm{e}^{−\mathrm{2}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}\mathrm{e}^{−\mathrm{iarctan2}} }\right)^{\mathrm{a}} .\Gamma\left(\mathrm{a}+\mathrm{3}\right) \\ $$$$=\mathrm{e}^{\mathrm{i}\pi\mathrm{a}} \:\mathrm{e}^{−\mathrm{2}} \:\mathrm{5}^{\frac{\mathrm{a}}{\mathrm{2}}} \:\mathrm{e}^{\mathrm{iaarctan2}\:} .\Gamma\left(\mathrm{a}+\mathrm{3}\right)\:\:\mathrm{rest}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{f}^{'} \left(\mathrm{0}\right)....\mathrm{be}\:\mathrm{continued}... \\ $$
