Math Question and Answers


Question and Answers Forum

All Questions Topic List
Mechanics Questions
Previous in All Question Next in All Question
Previous in Mechanics Next in Mechanics
Question Number 161783 by ajfour last updated on 22/Dec/21

Commented by ajfour last updated on 22/Dec/21

$C y l i n d e r i s f r e e t o p u r e l y r o l l, f i n d$ $r a d i u s, i f p o i n t m a s s b a l l i s t o b e$ $r e c e i v e d s u c c e s s f u l l y .$
Commented by ajfour last updated on 22/Dec/21
Left d job, shall hunt online..
Commented by mr W last updated on 22/Dec/21

$w e l c o m e b a c k s i r!$
Commented by ajfour last updated on 22/Dec/21

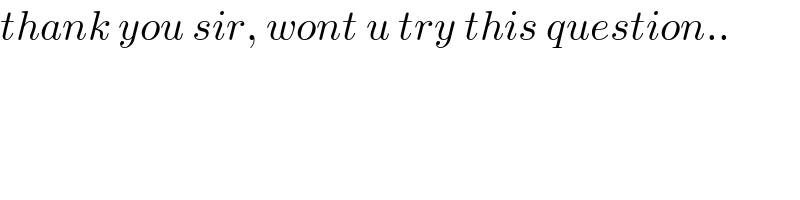
$t h a n k y o u s i r, w o n t u t r y t h i s q u e s t i o n . .$
Commented by mr W last updated on 23/Dec/21

$i^{'} l l t r y h o w f a r i c a n g o .$
	Answered by mr W last updated on 23/Dec/21

	Commented by mr W last updated on 23/Dec/21

	$x_{1} = s$ $φ = \frac{s}{R}$ $l e t ω = \frac{d θ}{d t}$ $x_{2} = s - R \sin θ$ $y_{2} = R (1 + \cos θ)$ $V = \frac{d s}{d t} = ω \frac{d s}{d θ}$ $A = \frac{d V}{d t} = ω \frac{d V}{d θ}$ $N \sin θ R = (\frac{{M R}^{2}}{2} + {M R}^{2}) (\frac{A}{R})$ $\Rightarrow N = \frac{3 M A}{2 \sin θ} = \frac{3 M}{2 \sin θ} \times \frac{ω d V}{d θ}$ $N = 0 \Leftrightarrow \frac{d V}{d θ} = 0$ $v_{x} = \frac{{d x}_{2}}{d t} = V - R \cos θ ω$ $v_{y} = \frac{{d y}_{2}}{d t} = - R \sin θ ω$ $\frac{m}{2} (v_{x}^{2} + v_{y}^{2}) + \frac{1}{2} \times \frac{3 {M R}^{2}}{2} \times {(\frac{V}{R})}^{2} = m g R (1 - \cos θ)$ $v_{x}^{2} + v_{y}^{2} + \frac{3 {M V}^{2}}{2 m} = 2 g R (1 - \cos θ)$ $V^{2} + R^{2} ω^{2} - 2 V R ω \cos θ + \frac{3 {M V}^{2}}{2 m} = 2 g R (1 - \cos θ)$ $ω^{2} - \frac{2 g (1 - \cos θ)}{R} - 2 ω \cos θ (\frac{V}{R}) + (\frac{3 M}{2 m} + 1) {(\frac{V}{R})}^{2} = 0$ $\Rightarrow \frac{V}{R} = \frac{ω \cos θ + \sqrt{ω^{2} (\cos^{2} θ - μ) + \frac{2 μ g (1 - \cos θ)}{R}}}{μ}$ $w i t h μ = \frac{3 M}{2 m} + 1$ $\frac{ω d s}{R d θ} = \frac{ω \cos θ + \sqrt{ω^{2} (\cos^{2} θ - μ) + \frac{2 μ g (1 - \cos θ)}{R}}}{μ}$ $\frac{d s}{d θ} = R \times \frac{\cos θ + \sqrt{\cos^{2} θ - μ + \frac{2 μ g (1 - \cos θ)}{R ω^{2}}}}{μ}$ $\Rightarrow s = R \int_{0}^{θ} \frac{\cos θ + \sqrt{\cos^{2} θ - μ + \frac{2 μ g (1 - \cos θ)}{R ω^{2}}}}{μ} d θ$ $a_{x} = \frac{{d v}_{x}}{d t} = \frac{ω d}{d θ} (V - R \cos θ ω) = ω (\frac{d V}{d θ} - R \cos θ \frac{d ω}{d θ} + R \sin θ ω)$ $a_{y} = \frac{{d v}_{y}}{d t} = \frac{ω d}{d θ} (- R \sin θ ω) = ω (- R \sin θ \frac{d ω}{d θ} - R \cos θ ω)$ ${m a}_{x} = - N \sin θ$ $m ω (\frac{d V}{d θ} - R \cos θ \frac{d ω}{d θ} + R \sin θ ω) = - \frac{3 M}{2} \times \frac{ω d V}{d θ}$ $\Rightarrow μ \frac{d}{d θ} (\frac{V}{R}) - \cos θ \frac{d ω}{d θ} + \sin θ ω = 0$ ${m a}_{y} = N \cos θ - m g$ $m ω (- R \sin θ \frac{d ω}{d θ} - R \cos θ ω) = \frac{3 M}{2 \sin θ} \times \frac{ω d V}{d θ} \cos θ - m g$ $\Rightarrow \frac{3 M}{2 m} \times \frac{d}{d θ} (\frac{V}{R}) = \frac{g}{ω R} - (\sin θ \frac{d ω}{d θ} + \cos θ ω) \tan θ$ $\frac{3 M}{2 m μ} \cos θ \frac{d ω}{d θ} - \frac{3 M}{2 m μ} \sin θ ω = \frac{g}{ω R} - \frac{\sin^{2} θ}{\cos θ} \frac{d ω}{d θ} - \sin θ ω$ $\begin{matrix} (\frac{3 M}{3 M + 2 m} + \tan^{2} θ) \cos θ \frac{d ω}{d θ} - (\frac{2 m}{3 M + 2 m}) \sin θ ω - \frac{g}{ω R} = 0 \end{matrix}$ $s o l v e t h i s d . e . (h a r d t o d o!) f o r ω = f (θ)$ $u n d e r ω = 0 a t θ = 0$ $. . . . . . .$ $o n c e w e h a v e ω = f (θ), w e a l s o g e t \frac{V}{R} .$ $f r o m \frac{d}{d θ} (\frac{V}{R}) = 0 w e g e t θ_{1} a t w h i c h t h e$ $s m a l l b a l l l o s e s c o n t a c t t o c y l i n d e r .$ $w e a l s o g e t t h e v_{x} a n d v_{y} a t t h i s i n s t a n t .$ $u p o n n o w t h e s m a l l b a l l h a s t h e$ $m o t i o n o f p r o j e c t i l e a n d w e c a n f i n d$ $t h e p o s i t i o n w h e r e i t h i t s t h e g r o u n d .$
	Commented by mr W last updated on 23/Dec/21

	${t h a t}^{'} s t h e p o i n t i c a n m a x i m a l l y c o m e$ $t o .$
	Commented by Tawa11 last updated on 23/Dec/21

	$Great sir$
	Commented by ajfour last updated on 23/Dec/21
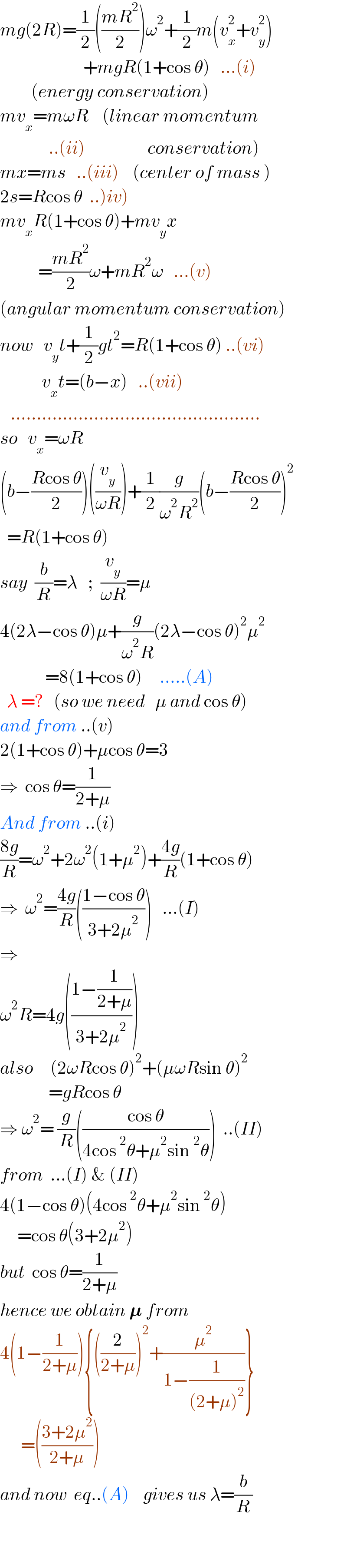
	$mg(2R)=(1/2)(((mR^2 )/2))ω^2 +(1/2)m(v_x ^2 +v_y ^2 ) +mgR(1+cos θ) ...(i) (energy conservation) mv_x =mωR (linear momentum ..(ii) conservation) mx=ms ..(iii) (center of mass ) 2s=Rcos θ ..)iv) mv_x R(1+cos θ)+mv_y x =((mR^2 )/2)ω+mR^2 ω ...(v) (angular momentum conservation) now v_y t+(1/2)gt^2 =R(1+cos θ) ..(vi) v_x t=(b−x) ..(vii) ................................................ so v_x =ωR (b−((Rcos θ)/2))((v_y /(ωR)))+(1/2)(g/(ω^2 R^2 ))(b−((Rcos θ)/2))^2 =R(1+cos θ) say (b/R)=λ ; (v_y /(ωR))=μ 4(2λ−cos θ)μ+(g/(ω^2 R))(2λ−cos θ)^2 μ^2 =8(1+cos θ) .....(A) λ =? (so we need μ and cos θ) and from ..(v) 2(1+cos θ)+μcos θ=3 ⇒ cos θ=(1/(2+μ)) And from ..(i) ((8g)/R)=ω^2 +2ω^2 (1+μ^2 )+((4g)/R)(1+cos θ) ⇒ ω^2 =((4g)/R)(((1−cos θ)/(3+2μ^2 ))) ...(I) ⇒ ω^2 R=4g(((1−(1/(2+μ)))/(3+2μ^2 ))) also (2ωRcos θ)^2 +(μωRsin θ)^2 =gRcos θ ⇒ ω^2 = (g/R)(((cos θ)/(4cos^2 θ+μ^2 sin^2 θ))) ..(II) from ...(I) & (II) 4(1−cos θ)(4cos^2 θ+μ^2 sin^2 θ) =cos θ(3+2μ^2 ) but cos θ=(1/(2+μ)) hence we obtain 𝛍 from 4(1−(1/(2+μ))){((2/(2+μ)))^2 +(μ^2 /(1−(1/((2+μ)^2 ))))} =(((3+2μ^2 )/(2+μ))) and now eq..(A) gives us λ=(b/R)$
	$m g (2 R) = \frac{1}{2} (\frac{{m R}^{2}}{2}) ω^{2} + \frac{1}{2} m (v_{x}^{2} + v_{y}^{2})$ $+ m g R (1 + \cos θ) . . . (i)$ $(e n e r g y c o n s e r v a t i o n)$ ${m v}_{x} = m ω R (l i n e a r m o m e n t u m$ $. . (i i) c o n s e r v a t i o n)$ $m x = m s . . (i i i) (c e n t e r o f m a s s)$ $2 s = R \cos θ . .) i v)$ ${m v}_{x} R (1 + \cos θ) + {m v}_{y} x$ $= \frac{{m R}^{2}}{2} ω + {m R}^{2} ω . . . (v)$ $(a n g u l a r m o m e n t u m c o n s e r v a t i o n)$ $n o w v_{y} t + \frac{1}{2} {g t}^{2} = R (1 + \cos θ) . . (v i)$ $v_{x} t = (b - x) . . (v i i)$ $. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .$ $s o v_{x} = ω R$ $(b - \frac{R \cos θ}{2}) (\frac{v_{y}}{ω R}) + \frac{1}{2} \frac{g}{ω^{2} R^{2}} {(b - \frac{R \cos θ}{2})}^{2}$ $= R (1 + \cos θ)$ $s a y \frac{b}{R} = λ; \frac{v_{y}}{ω R} = μ$ $4 (2 λ - \cos θ) μ + \frac{g}{ω^{2} R} {(2 λ - \cos θ)}^{2} μ^{2}$ $= 8 (1 + \cos θ) . . . . . (A)$ $λ = ? (s o w e n e e d μ a n d \cos θ)$ $a n d f r o m . . (v)$ $2 (1 + \cos θ) + μ \cos θ = 3$ $\Rightarrow \cos θ = \frac{1}{2 + μ}$ $A n d f r o m . . (i)$ $\frac{8 g}{R} = ω^{2} + 2 ω^{2} (1 + μ^{2}) + \frac{4 g}{R} (1 + \cos θ)$ $\Rightarrow ω^{2} = \frac{4 g}{R} (\frac{1 - \cos θ}{3 + 2 μ^{2}}) . . . (I)$ $\Rightarrow$ $ω^{2} R = 4 g (\frac{1 - \frac{1}{2 + μ}}{3 + 2 μ^{2}})$ $a l s o {(2 ω R \cos θ)}^{2} + {(μ ω R \sin θ)}^{2}$ $= g R \cos θ$ $\Rightarrow ω^{2} = \frac{g}{R} (\frac{\cos θ}{4 \cos^{2} θ + μ^{2} \sin^{2} θ}) . . (I I)$ $f r o m . . . (I) & (I I)$ $4 (1 - \cos θ) (4 \cos^{2} θ + μ^{2} \sin^{2} θ)$ $= \cos θ (3 + 2 μ^{2})$ $b u t \cos θ = \frac{1}{2 + μ}$ $h e n c e w e o b t a i n μ f r o m$ $4 (1 - \frac{1}{2 + μ}) {{(\frac{2}{2 + μ})}^{2} + \frac{μ^{2}}{1 - \frac{1}{{(2 + μ)}^{2}}}}$ $= (\frac{3 + 2 μ^{2}}{2 + μ})$ $a n d n o w e q . . (A) g i v e s u s λ = \frac{b}{R}$
	Commented by mr W last updated on 23/Dec/21

	$g r e a t!$ $i n e e d s o m e t i m e t o f o l l o w i t .$ $i t h i n k w i t h ω y o u {d o n}^{'} t m e a n$ $ω = \frac{d θ}{d t}, r i g h t ?$
	Commented by ajfour last updated on 23/Dec/21

	$y e a h i t s n o t \frac{d θ}{d t}, i t s t h e a n g u l a r$ $v e l o c i t y o f r o t a t i o n o f t h e c y l i n d e r .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum