Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 161964 by HongKing last updated on 24/Dec/21

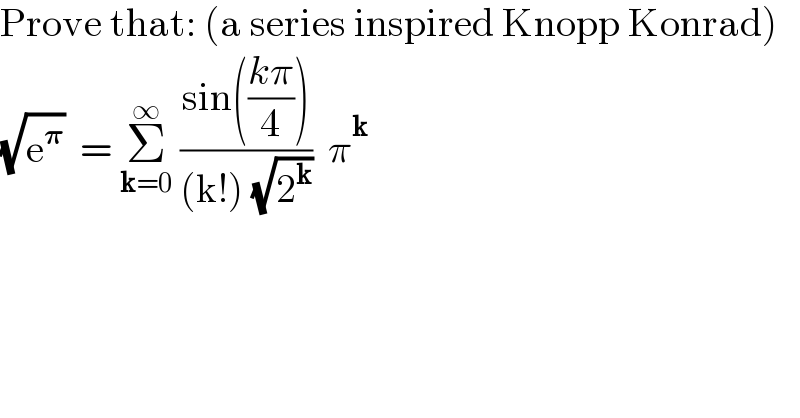
Prove that: (a series inspired Knopp Konrad) (√e^𝛑 ) = Σ_(k=0) ^∞ ((sin(((kπ)/4)))/((k!) (√2^k ))) π^k

$$\mathrm{Prove}\:\mathrm{that}:\:\left(\mathrm{a}\:\mathrm{series}\:\mathrm{inspired}\:\mathrm{Knopp}\:\mathrm{Konrad}\right) \\ $$$$\sqrt{\mathrm{e}^{\boldsymbol{\pi}} }\:\:=\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{4}}\right)}{\left(\mathrm{k}!\right)\:\sqrt{\mathrm{2}^{\boldsymbol{\mathrm{k}}} }}\:\:\pi^{\boldsymbol{\mathrm{k}}} \\ $$

Answered by mindispower last updated on 25/Dec/21

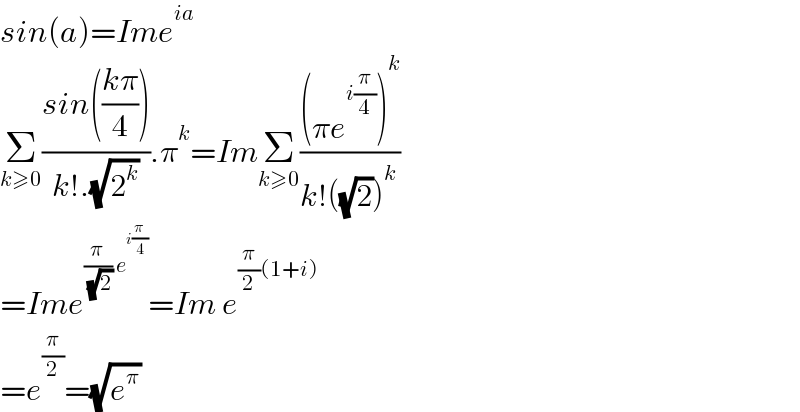
sin(a)=Ime^(ia) Σ_(k≥0) ((sin(((kπ)/4)))/(k!.(√2^k ))).π^k =ImΣ_(k≥0) (((πe^(i(π/4)) )^k )/(k!((√2))^k )) =Ime^((π/( (√2))) e^(i(π/4)) ) =Im e^((π/2)(1+i)) =e^(π/2) =(√e^π )

$${sin}\left({a}\right)={Ime}^{{ia}} \\ $$$$\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{sin}\left(\frac{{k}\pi}{\mathrm{4}}\right)}{{k}!.\sqrt{\mathrm{2}^{{k}} }}.\pi^{{k}} ={Im}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(\pi{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)^{{k}} }{{k}!\left(\sqrt{\mathrm{2}}\right)^{{k}} } \\ $$$$={Ime}^{\frac{\pi}{\:\sqrt{\mathrm{2}}}\:{e}^{{i}\frac{\pi}{\mathrm{4}}} } ={Im}\:{e}^{\frac{\pi}{\mathrm{2}}\left(\mathrm{1}+{i}\right)} \\ $$$$={e}^{\frac{\pi}{\mathrm{2}}} =\sqrt{{e}^{\pi} } \\ $$

Commented by HongKing last updated on 25/Dec/21

cool my dear Sir thank you so much

$$\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Answered by Lordose last updated on 25/Dec/21

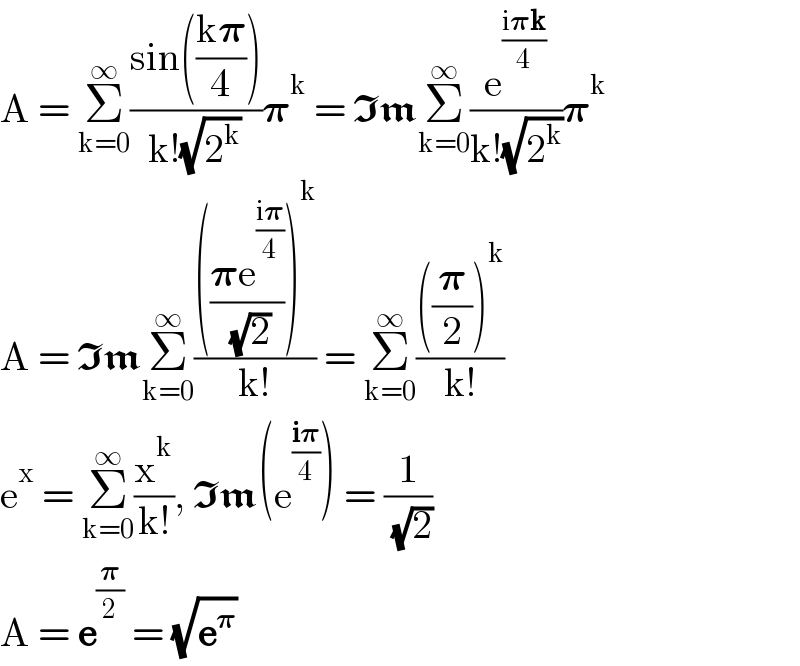
A = Σ_(k=0) ^∞ ((sin(((k𝛑)/4)))/(k!(√2^k )))𝛑^k = ImΣ_(k=0) ^∞ (e^((i𝛑k)/4) /(k!(√2^k )))𝛑^k A = ImΣ_(k=0) ^∞ (((((𝛑e^((i𝛑)/4) )/( (√2))))^k )/(k!)) = Σ_(k=0) ^∞ ((((𝛑/2))^k )/(k!)) e^x = Σ_(k=0) ^∞ (x^k /(k!)), Im(e^((i𝛑)/4) ) = (1/( (√2))) A = e^(𝛑/2) = (√e^𝛑 )

$$\mathrm{A}\:=\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\frac{\mathrm{k}\boldsymbol{\pi}}{\mathrm{4}}\right)}{\mathrm{k}!\sqrt{\mathrm{2}^{\mathrm{k}} }}\boldsymbol{\pi}^{\mathrm{k}} \:=\:\boldsymbol{\mathfrak{Im}}\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{e}^{\frac{\mathrm{i}\boldsymbol{\pi\mathrm{k}}}{\mathrm{4}}} }{\mathrm{k}!\sqrt{\mathrm{2}^{\mathrm{k}} }}\boldsymbol{\pi}^{\mathrm{k}} \\ $$$$\mathrm{A}\:=\:\boldsymbol{\mathfrak{Im}}\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\boldsymbol{\pi}\mathrm{e}^{\frac{\mathrm{i}\boldsymbol{\pi}}{\mathrm{4}}} }{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{k}} }{\mathrm{k}!}\:=\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\boldsymbol{\pi}}{\mathrm{2}}\right)^{\mathrm{k}} }{\mathrm{k}!} \\ $$$$\mathrm{e}^{\mathrm{x}} \:=\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{k}} }{\mathrm{k}!},\:\boldsymbol{\mathfrak{Im}}\left(\mathrm{e}^{\frac{\boldsymbol{\mathrm{i}\pi}}{\mathrm{4}}} \right)\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{A}\:=\:\boldsymbol{\mathrm{e}}^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \:=\:\sqrt{\boldsymbol{\mathrm{e}}^{\boldsymbol{\pi}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com