Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 162015 by mathmax by abdo last updated on 25/Dec/21

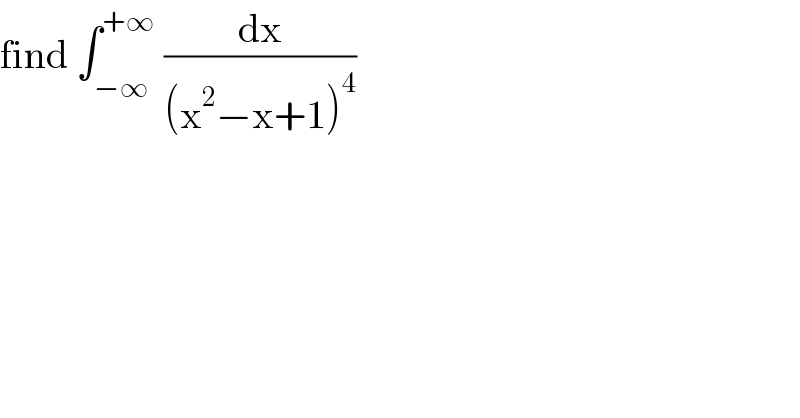
find ∫_(−∞) ^(+∞) (dx/((x^2 −x+1)^4 ))

$$\mathrm{find}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$

Answered by MJS_new last updated on 25/Dec/21

∫_(−∞) ^(+∞) (dx/((x^2 −x+1)^4 ))= [Ostrogradski′s Method] =[(((2x−1)(10x^4 −20x^3 +35x^2 −25x+18))/(27(x^2 −x+1)^3 ))]_(−∞) ^(+∞) +((20)/(27))∫_(−∞) ^(+∞) (dx/(x^2 −x+1))= =0+((40(√3))/(81))[arctan ((2x−1)/( (√3)))]_(−∞) ^(+∞) = =((40(√3)π)/(81))

$$\underset{−\infty} {\overset{+\infty} {\int}}\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{4}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\left[\frac{\left(\mathrm{2}{x}−\mathrm{1}\right)\left(\mathrm{10}{x}^{\mathrm{4}} −\mathrm{20}{x}^{\mathrm{3}} +\mathrm{35}{x}^{\mathrm{2}} −\mathrm{25}{x}+\mathrm{18}\right)}{\mathrm{27}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{3}} }\right]_{−\infty} ^{+\infty} +\frac{\mathrm{20}}{\mathrm{27}}\underset{−\infty} {\overset{+\infty} {\int}}\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}= \\ $$$$=\mathrm{0}+\frac{\mathrm{40}\sqrt{\mathrm{3}}}{\mathrm{81}}\left[\mathrm{arctan}\:\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right]_{−\infty} ^{+\infty} = \\ $$$$=\frac{\mathrm{40}\sqrt{\mathrm{3}}\pi}{\mathrm{81}} \\ $$

Commented by mathmax by abdo last updated on 25/Dec/21

thanks sir

$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Answered by mathmax by abdo last updated on 25/Dec/21

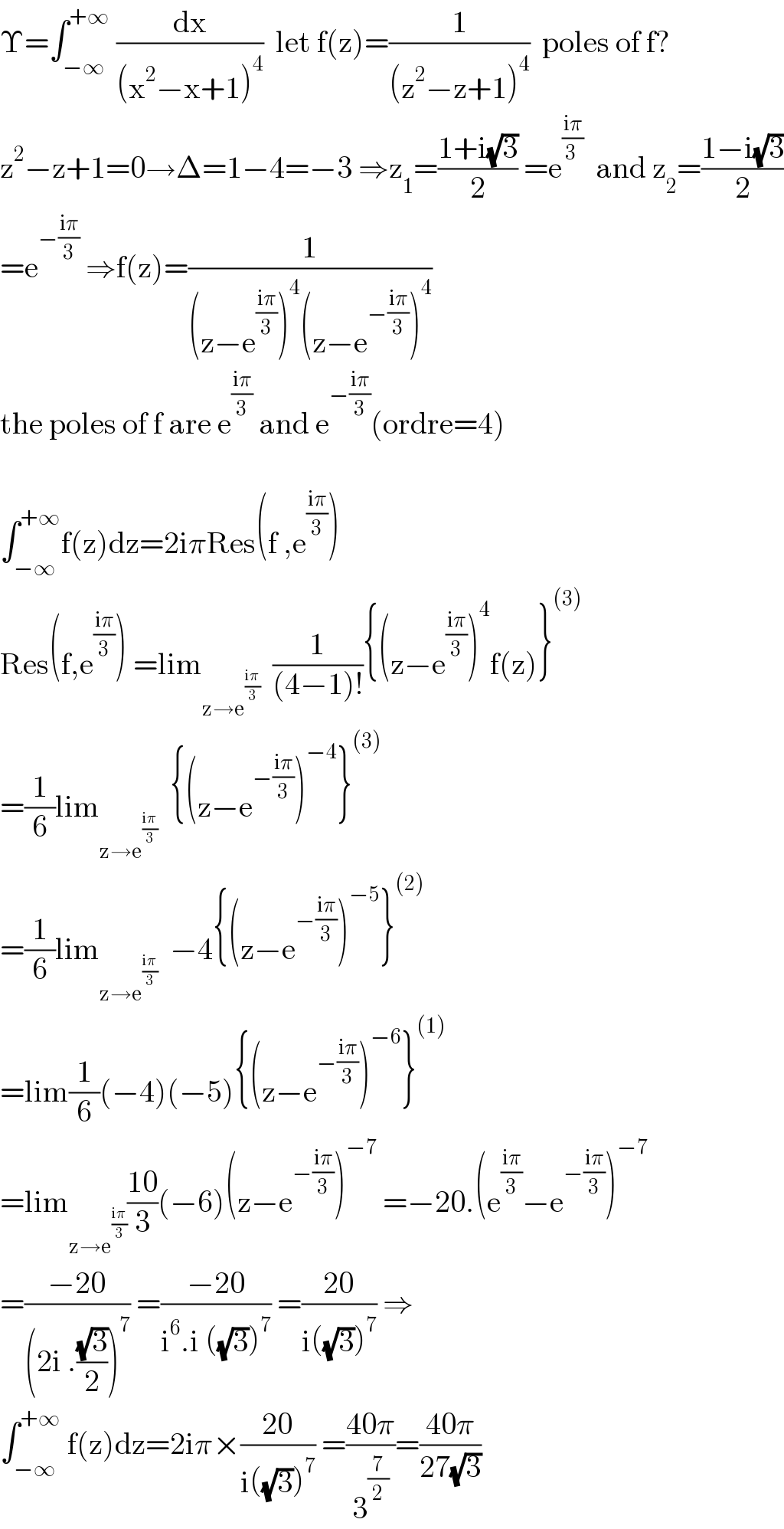
Υ=∫_(−∞) ^(+∞) (dx/((x^2 −x+1)^4 )) let f(z)=(1/((z^2 −z+1)^4 )) poles of f? z^2 −z+1=0→Δ=1−4=−3 ⇒z_1 =((1+i(√3))/2) =e^((iπ)/(3 )) and z_2 =((1−i(√3))/2) =e^(−((iπ)/3)) ⇒f(z)=(1/((z−e^((iπ)/3) )^4 (z−e^(−((iπ)/3)) )^4 )) the poles of f are e^((iπ)/3) and e^(−((iπ)/3)) (ordre=4) ∫_(−∞) ^(+∞) f(z)dz=2iπRes(f ,e^((iπ)/3) ) Res(f,e^((iπ)/3) ) =lim_(z→e^((iπ)/3) ) (1/((4−1)!)){(z−e^((iπ)/3) )^4 f(z)}^((3)) =(1/6)lim_(z→e^((iπ)/3) ) {(z−e^(−((iπ)/3)) )^(−4) }^((3)) =(1/6)lim_(z→e^((iπ)/3) ) −4{(z−e^(−((iπ)/3)) )^(−5) }^((2)) =lim(1/6)(−4)(−5){(z−e^(−((iπ)/3)) )^(−6) }^((1)) =lim_(z→e^((iπ)/3) ) ((10)/3)(−6)(z−e^(−((iπ)/3)) )^(−7) =−20.(e^((iπ)/3) −e^(−((iπ)/3)) )^(−7) =((−20)/((2i .((√3)/2))^7 )) =((−20)/(i^6 .i ((√3))^7 )) =((20)/(i((√3))^7 )) ⇒ ∫_(−∞) ^(+∞) f(z)dz=2iπ×((20)/(i((√3))^7 )) =((40π)/3^(7/2) )=((40π)/(27(√3)))

$$\Upsilon=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\right)^{\mathrm{4}} }\:\:\mathrm{poles}\:\mathrm{of}\:\mathrm{f}? \\ $$$$\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}=\mathrm{0}\rightarrow\Delta=\mathrm{1}−\mathrm{4}=−\mathrm{3}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}\:}} \:\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$=\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\Rightarrow\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} \left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} } \\ $$$$\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:\mathrm{f}\:\mathrm{are}\:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \left(\mathrm{ordre}=\mathrm{4}\right) \\ $$$$ \\ $$$$\int_{−\infty} ^{+\infty} \mathrm{f}\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi\mathrm{Res}\left(\mathrm{f}\:,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right) \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\frac{\mathrm{1}}{\left(\mathrm{4}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} \mathrm{f}\left(\mathrm{z}\right)\right\}^{\left(\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\left\{\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{−\mathrm{4}} \right\}^{\left(\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:−\mathrm{4}\left\{\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{−\mathrm{5}} \right\}^{\left(\mathrm{2}\right)} \\ $$$$=\mathrm{lim}\frac{\mathrm{1}}{\mathrm{6}}\left(−\mathrm{4}\right)\left(−\mathrm{5}\right)\left\{\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{−\mathrm{6}} \right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \frac{\mathrm{10}}{\mathrm{3}}\left(−\mathrm{6}\right)\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{−\mathrm{7}} \:=−\mathrm{20}.\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{−\mathrm{7}} \\ $$$$=\frac{−\mathrm{20}}{\left(\mathrm{2i}\:.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{7}} }\:=\frac{−\mathrm{20}}{\mathrm{i}^{\mathrm{6}} .\mathrm{i}\:\left(\sqrt{\mathrm{3}}\right)^{\mathrm{7}} }\:=\frac{\mathrm{20}}{\mathrm{i}\left(\sqrt{\mathrm{3}}\right)^{\mathrm{7}} }\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\mathrm{f}\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi×\frac{\mathrm{20}}{\mathrm{i}\left(\sqrt{\mathrm{3}}\right)^{\mathrm{7}} }\:=\frac{\mathrm{40}\pi}{\mathrm{3}^{\frac{\mathrm{7}}{\mathrm{2}}} }=\frac{\mathrm{40}\pi}{\mathrm{27}\sqrt{\mathrm{3}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com