Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 162118 by SANOGO last updated on 27/Dec/21

determiner le reste de la division euclidienne de 10^(100) par 105

$${determiner}\:{le}\:{reste}\:{de}\:{la}\:{division}\:{euclidienne}\:{de} \\ $$$$\mathrm{10}^{\mathrm{100}} \:{par}\:\mathrm{105} \\ $$

Commented by SANOGO last updated on 27/Dec/21

thank you

$${thank}\:{you} \\ $$

Commented by SANOGO last updated on 27/Dec/21

merci bien

$${merci}\:{bien} \\ $$

Commented by mr W last updated on 27/Dec/21

in following stupid method with “=^R ” i mean “has the same remainder as”. 10^(100) =10×10^(99) =10×(1000)^(33) =10×(9×105+55)^(33) =^R 10×55^(33) =10×55×(3025)^(16) =10×55×(28×105+85)^(16) =^R 10×55×85^(16) =10×55×(68×105+85)^8 =^R 10×55×85^8 =^R 10×55×85^4 =^R 10×55×85^2 =^R 10×55×85 =^R 25 i.e. the remainder is 25 when 10^(100) is divided by 105.

$${in}\:{following}\:{stupid}\:{method}\: \\ $$$${with}\:``\overset{{R}} {=}''\:{i}\:{mean} \\ $$$$``{has}\:{the}\:{same}\:{remainder}\:{as}''. \\ $$$$\mathrm{10}^{\mathrm{100}} =\mathrm{10}×\mathrm{10}^{\mathrm{99}} =\mathrm{10}×\left(\mathrm{1000}\right)^{\mathrm{33}} \\ $$$$=\mathrm{10}×\left(\mathrm{9}×\mathrm{105}+\mathrm{55}\right)^{\mathrm{33}} \\ $$$$\overset{{R}} {=}\mathrm{10}×\mathrm{55}^{\mathrm{33}} =\mathrm{10}×\mathrm{55}×\left(\mathrm{3025}\right)^{\mathrm{16}} \\ $$$$=\mathrm{10}×\mathrm{55}×\left(\mathrm{28}×\mathrm{105}+\mathrm{85}\right)^{\mathrm{16}} \\ $$$$\overset{{R}} {=}\mathrm{10}×\mathrm{55}×\mathrm{85}^{\mathrm{16}} =\mathrm{10}×\mathrm{55}×\left(\mathrm{68}×\mathrm{105}+\mathrm{85}\right)^{\mathrm{8}} \\ $$$$\overset{{R}} {=}\mathrm{10}×\mathrm{55}×\mathrm{85}^{\mathrm{8}} \\ $$$$\overset{{R}} {=}\mathrm{10}×\mathrm{55}×\mathrm{85}^{\mathrm{4}} \\ $$$$\overset{{R}} {=}\mathrm{10}×\mathrm{55}×\mathrm{85}^{\mathrm{2}} \\ $$$$\overset{{R}} {=}\mathrm{10}×\mathrm{55}×\mathrm{85} \\ $$$$\overset{{R}} {=}\mathrm{25} \\ $$$${i}.{e}.\:{the}\:{remainder}\:{is}\:\mathrm{25}\:{when}\:\mathrm{10}^{\mathrm{100}} \\ $$$${is}\:{divided}\:{by}\:\mathrm{105}. \\ $$

Commented by Rasheed.Sindhi last updated on 27/Dec/21

∨ ∩i⊂∈ sir! If your ′stupid′ method is so wonderful what your ′wonderful′ method will be!!!

$$\vee\:\cap\mathrm{i}\subset\in\:\boldsymbol{\mathrm{sir}}!\: \\ $$$${If}\:{your}\:'{stupid}'\:{method}\:{is}\:{so}\:{wonderful} \\ $$$${what}\:{your}\:'{wonderful}'\:{method}\:{will}\:{be}!!! \\ $$

Commented by Rasheed.Sindhi last updated on 27/Dec/21

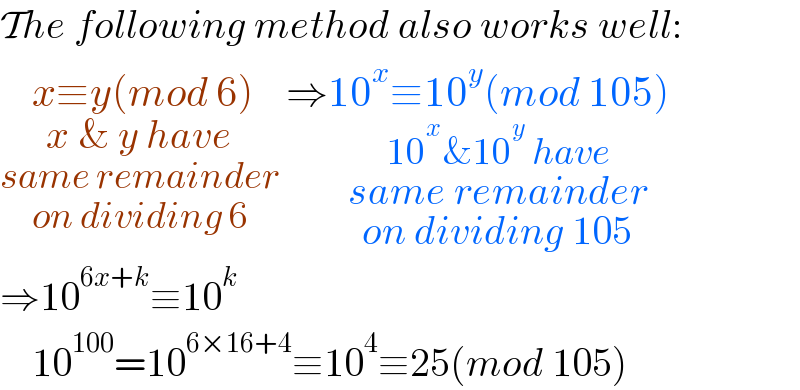
The following method also works well: x≡y(mod 6)_(x & y have_(same remainder_(on dividing 6) ) ) ⇒10^x ≡10^y (mod 105)_(10^x &10^y have_(same remainder_(on dividing 105) ) ) ⇒10^(6x+k) ≡10^k 10^(100) =10^(6×16+4) ≡10^4 ≡25(mod 105)

$$\mathcal{T}{he}\:{following}\:{method}\:{also}\:{works}\:{well}: \\ $$$$\underset{\underset{\underset{{on}\:{dividing}\:\mathrm{6}} {{same}\:{remainder}}} {{x}\:\&\:{y}\:{have}}\:} {{x}\equiv{y}\left({mod}\:\mathrm{6}\right)}\Rightarrow\underset{\underset{\underset{{on}\:{dividing}\:\mathrm{105}} {{same}\:{remainder}}} {\mathrm{10}^{{x}} \&\mathrm{10}^{{y}} \:{have}}} {\mathrm{10}^{{x}} \equiv\mathrm{10}^{{y}} \left({mod}\:\mathrm{105}\right)} \\ $$$$\Rightarrow\mathrm{10}^{\mathrm{6}{x}+{k}} \equiv\mathrm{10}^{{k}} \\ $$$$\:\:\:\:\mathrm{10}^{\mathrm{100}} =\mathrm{10}^{\mathrm{6}×\mathrm{16}+\mathrm{4}} \equiv\mathrm{10}^{\mathrm{4}} \equiv\mathrm{25}\left({mod}\:\mathrm{105}\right) \\ $$

Commented by mr W last updated on 27/Dec/21

this is a smart method!

$${this}\:{is}\:{a}\:{smart}\:{method}! \\ $$

Commented by Rasheed.Sindhi last updated on 27/Dec/21

Thanks sir!

$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\boldsymbol{\mathrm{sir}}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com