Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 16214 by Tinkutara last updated on 19/Jun/17

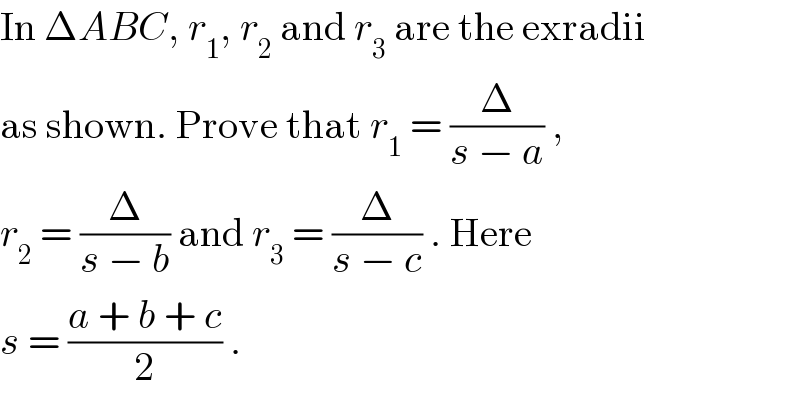
In ΔABC, r_1 , r_2 and r_3 are the exradii as shown. Prove that r_1 = (Δ/(s − a)) , r_2 = (Δ/(s − b)) and r_3 = (Δ/(s − c)) . Here s = ((a + b + c)/2) .

$$\mathrm{In}\:\Delta{ABC},\:{r}_{\mathrm{1}} ,\:{r}_{\mathrm{2}} \:\mathrm{and}\:{r}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{the}\:\mathrm{exradii} \\ $$$$\mathrm{as}\:\mathrm{shown}.\:\mathrm{Prove}\:\mathrm{that}\:{r}_{\mathrm{1}} \:=\:\frac{\Delta}{{s}\:−\:{a}}\:, \\ $$$${r}_{\mathrm{2}} \:=\:\frac{\Delta}{{s}\:−\:{b}}\:\mathrm{and}\:{r}_{\mathrm{3}} \:=\:\frac{\Delta}{{s}\:−\:{c}}\:.\:\mathrm{Here} \\ $$$${s}\:=\:\frac{{a}\:+\:{b}\:+\:{c}}{\mathrm{2}}\:. \\ $$

Commented by Tinkutara last updated on 19/Jun/17

Commented by Tinkutara last updated on 20/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

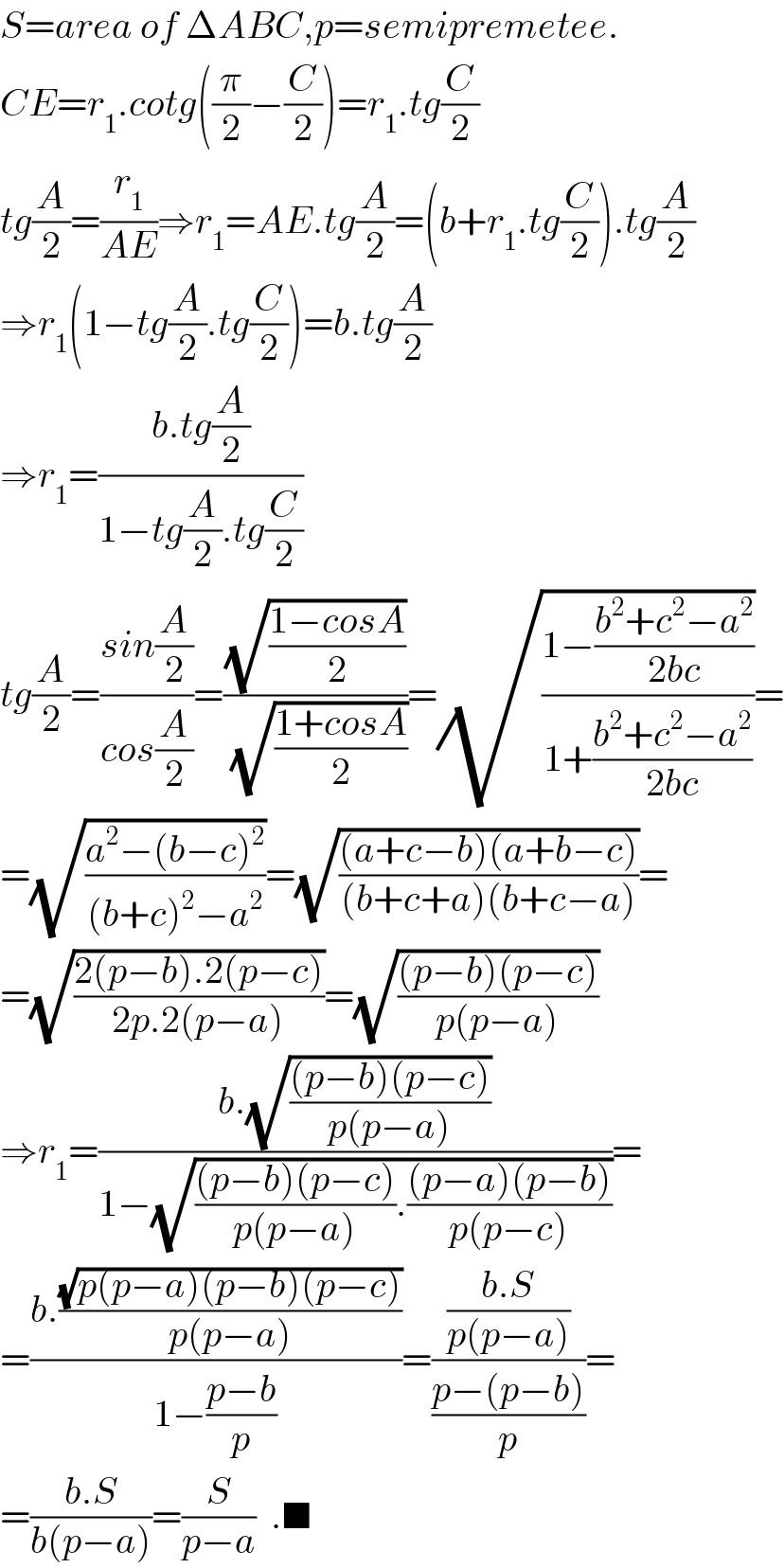
S=area of ΔABC,p=semipremetee. CE=r_1 .cotg((π/2)−(C/2))=r_1 .tg(C/2) tg(A/2)=(r_1 /(AE))⇒r_1 =AE.tg(A/2)=(b+r_1 .tg(C/2)).tg(A/2) ⇒r_1 (1−tg(A/2).tg(C/2))=b.tg(A/2) ⇒r_1 =((b.tg(A/2))/(1−tg(A/2).tg(C/2))) tg(A/2)=((sin(A/2))/(cos(A/2)))=((√((1−cosA)/2))/(√((1+cosA)/2)))=(√((1−((b^2 +c^2 −a^2 )/(2bc)))/(1+((b^2 +c^2 −a^2 )/(2bc)))))= =(√((a^2 −(b−c)^2 )/((b+c)^2 −a^2 )))=(√(((a+c−b)(a+b−c))/((b+c+a)(b+c−a))))= =(√((2(p−b).2(p−c))/(2p.2(p−a))))=(√(((p−b)(p−c))/(p(p−a)))) ⇒r_1 =((b.(√(((p−b)(p−c))/(p(p−a)))))/(1−(√((((p−b)(p−c))/(p(p−a))).(((p−a)(p−b))/(p(p−c)))))))= =((b.((√(p(p−a)(p−b)(p−c)))/(p(p−a))))/(1−((p−b)/p)))=(((b.S)/(p(p−a)))/((p−(p−b))/p))= =((b.S)/(b(p−a)))=(S/(p−a)) .■

$${S}={area}\:{of}\:\Delta{ABC},{p}={semipremetee}. \\ $$$${CE}={r}_{\mathrm{1}} .{cotg}\left(\frac{\pi}{\mathrm{2}}−\frac{{C}}{\mathrm{2}}\right)={r}_{\mathrm{1}} .{tg}\frac{{C}}{\mathrm{2}} \\ $$$${tg}\frac{{A}}{\mathrm{2}}=\frac{{r}_{\mathrm{1}} }{{AE}}\Rightarrow{r}_{\mathrm{1}} ={AE}.{tg}\frac{{A}}{\mathrm{2}}=\left({b}+{r}_{\mathrm{1}} .{tg}\frac{{C}}{\mathrm{2}}\right).{tg}\frac{{A}}{\mathrm{2}} \\ $$$$\Rightarrow{r}_{\mathrm{1}} \left(\mathrm{1}−{tg}\frac{{A}}{\mathrm{2}}.{tg}\frac{{C}}{\mathrm{2}}\right)={b}.{tg}\frac{{A}}{\mathrm{2}} \\ $$$$\Rightarrow{r}_{\mathrm{1}} =\frac{{b}.{tg}\frac{{A}}{\mathrm{2}}}{\mathrm{1}−{tg}\frac{{A}}{\mathrm{2}}.{tg}\frac{{C}}{\mathrm{2}}} \\ $$$${tg}\frac{{A}}{\mathrm{2}}=\frac{{sin}\frac{{A}}{\mathrm{2}}}{{cos}\frac{{A}}{\mathrm{2}}}=\frac{\sqrt{\frac{\mathrm{1}−{cosA}}{\mathrm{2}}}}{\sqrt{\frac{\mathrm{1}+{cosA}}{\mathrm{2}}}}=\sqrt{\frac{\mathrm{1}−\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}}{\mathrm{1}+\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}}}= \\ $$$$=\sqrt{\frac{{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} }{\left({b}+{c}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }}=\sqrt{\frac{\left({a}+{c}−{b}\right)\left({a}+{b}−{c}\right)}{\left({b}+{c}+{a}\right)\left({b}+{c}−{a}\right)}}= \\ $$$$=\sqrt{\frac{\mathrm{2}\left({p}−{b}\right).\mathrm{2}\left({p}−{c}\right)}{\mathrm{2}{p}.\mathrm{2}\left({p}−{a}\right)}}=\sqrt{\frac{\left({p}−{b}\right)\left({p}−{c}\right)}{{p}\left({p}−{a}\right)}} \\ $$$$\Rightarrow{r}_{\mathrm{1}} =\frac{{b}.\sqrt{\frac{\left({p}−{b}\right)\left({p}−{c}\right)}{{p}\left({p}−{a}\right)}}}{\mathrm{1}−\sqrt{\frac{\left({p}−{b}\right)\left({p}−{c}\right)}{{p}\left({p}−{a}\right)}.\frac{\left({p}−{a}\right)\left({p}−{b}\right)}{{p}\left({p}−{c}\right)}}}= \\ $$$$=\frac{{b}.\frac{\sqrt{{p}\left({p}−{a}\right)\left({p}−{b}\right)\left({p}−{c}\right)}}{{p}\left({p}−{a}\right)}}{\mathrm{1}−\frac{{p}−{b}}{{p}}}=\frac{\frac{{b}.{S}}{{p}\left({p}−{a}\right)}}{\frac{{p}−\left({p}−{b}\right)}{{p}}}= \\ $$$$=\frac{{b}.{S}}{{b}\left({p}−{a}\right)}=\frac{{S}}{{p}−{a}}\:\:.\blacksquare \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

AD=AE=b+r_1 .tg(C/2) DE^2 =r_1 ^2 +r_1 ^2 −2r_1 ^2 cos(180−A)= =2r_1 ^2 (1+cosA)=4r_1 ^2 cos^2 (A/2)⇒ DE=2r_1 .cos(A/2) DE^2 =AD^2 +AD^2 −2AD^2 .cosA= =2AD^2 (1−cosA)=4AD^2 .sin^2 (A/2) ⇒DE=2AD.sin(A/2)=2r_1 .cos(A/2)⇒ b+r_1 .tg(C/2)=r_1 .cotg(A/2)⇒r_1 =((b.tg(A/2))/(1−tg(A/2).tg(C/2))) tg(A/2)=(S/(p(p−a))),tg(A/2).tg(C/2)=((p−b)/p) ⇒r_1 =(((b.S)/(p(p−a)))/(1−((p−b)/p)))=((b.S)/(b.(p−a)))=(S/(p−a)) .■ note: r_1 =p.tg(A/2),r_2 =p.tg(B/2),r_3 =p.tg(C/2) tg(A/2).tg(B/2).tg(C/2)=(√(((p−b)(p−c)(p−a)(p−c)(p−a)(p−b))/(p(p−a).p(p−b).p(p−c))))=(S/p^2 ) ⇒S=p^2 .tg(A/2).tg(B/2).tg(C/2)=p^2 .(r_1 /p).(r_2 /p).(r_3 /p) ⇒S.p=r_1 .r_2 .r_3 ⇒S.(p.r)=r.r_1 .r_2 .r_3 ⇒S^2 =r.r_1 .r_2 .r_3 ⇒S=(√(r.r_1 .r_2 .r_3 )) .

$${AD}={AE}={b}+{r}_{\mathrm{1}} .{tg}\frac{{C}}{\mathrm{2}} \\ $$$${DE}^{\mathrm{2}} ={r}_{\mathrm{1}} ^{\mathrm{2}} +{r}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{r}_{\mathrm{1}} ^{\mathrm{2}} {cos}\left(\mathrm{180}−{A}\right)= \\ $$$$=\mathrm{2}{r}_{\mathrm{1}} ^{\mathrm{2}} \left(\mathrm{1}+{cosA}\right)=\mathrm{4}{r}_{\mathrm{1}} ^{\mathrm{2}} {cos}^{\mathrm{2}} \frac{{A}}{\mathrm{2}}\Rightarrow \\ $$$${DE}=\mathrm{2}{r}_{\mathrm{1}} .{cos}\frac{{A}}{\mathrm{2}} \\ $$$${DE}^{\mathrm{2}} ={AD}^{\mathrm{2}} +{AD}^{\mathrm{2}} −\mathrm{2}{AD}^{\mathrm{2}} .{cosA}= \\ $$$$=\mathrm{2}{AD}^{\mathrm{2}} \left(\mathrm{1}−{cosA}\right)=\mathrm{4}{AD}^{\mathrm{2}} .{sin}^{\mathrm{2}} \frac{{A}}{\mathrm{2}} \\ $$$$\Rightarrow{DE}=\mathrm{2}{AD}.{sin}\frac{{A}}{\mathrm{2}}=\mathrm{2}{r}_{\mathrm{1}} .{cos}\frac{{A}}{\mathrm{2}}\Rightarrow \\ $$$${b}+{r}_{\mathrm{1}} .{tg}\frac{{C}}{\mathrm{2}}={r}_{\mathrm{1}} .{cotg}\frac{{A}}{\mathrm{2}}\Rightarrow{r}_{\mathrm{1}} =\frac{{b}.{tg}\frac{{A}}{\mathrm{2}}}{\mathrm{1}−{tg}\frac{{A}}{\mathrm{2}}.{tg}\frac{{C}}{\mathrm{2}}} \\ $$$${tg}\frac{{A}}{\mathrm{2}}=\frac{{S}}{{p}\left({p}−{a}\right)},{tg}\frac{{A}}{\mathrm{2}}.{tg}\frac{{C}}{\mathrm{2}}=\frac{{p}−{b}}{{p}} \\ $$$$\Rightarrow{r}_{\mathrm{1}} =\frac{\frac{{b}.{S}}{{p}\left({p}−{a}\right)}}{\mathrm{1}−\frac{{p}−{b}}{{p}}}=\frac{{b}.{S}}{{b}.\left({p}−{a}\right)}=\frac{{S}}{{p}−{a}}\:.\blacksquare \\ $$$${note}:\:{r}_{\mathrm{1}} ={p}.{tg}\frac{{A}}{\mathrm{2}},{r}_{\mathrm{2}} ={p}.{tg}\frac{{B}}{\mathrm{2}},{r}_{\mathrm{3}} ={p}.{tg}\frac{{C}}{\mathrm{2}} \\ $$$${tg}\frac{{A}}{\mathrm{2}}.{tg}\frac{{B}}{\mathrm{2}}.{tg}\frac{{C}}{\mathrm{2}}=\sqrt{\frac{\left({p}−{b}\right)\left({p}−{c}\right)\left({p}−{a}\right)\left({p}−{c}\right)\left({p}−{a}\right)\left({p}−{b}\right)}{{p}\left({p}−{a}\right).{p}\left({p}−{b}\right).{p}\left({p}−{c}\right)}}=\frac{{S}}{{p}^{\mathrm{2}} } \\ $$$$\Rightarrow{S}={p}^{\mathrm{2}} .{tg}\frac{{A}}{\mathrm{2}}.{tg}\frac{{B}}{\mathrm{2}}.{tg}\frac{{C}}{\mathrm{2}}={p}^{\mathrm{2}} .\frac{{r}_{\mathrm{1}} }{{p}}.\frac{{r}_{\mathrm{2}} }{{p}}.\frac{{r}_{\mathrm{3}} }{{p}} \\ $$$$\Rightarrow{S}.{p}={r}_{\mathrm{1}} .{r}_{\mathrm{2}} .{r}_{\mathrm{3}} \Rightarrow{S}.\left({p}.{r}\right)={r}.{r}_{\mathrm{1}} .{r}_{\mathrm{2}} .{r}_{\mathrm{3}} \\ $$$$\Rightarrow{S}^{\mathrm{2}} ={r}.{r}_{\mathrm{1}} .{r}_{\mathrm{2}} .{r}_{\mathrm{3}} \Rightarrow{S}=\sqrt{{r}.{r}_{\mathrm{1}} .{r}_{\mathrm{2}} .{r}_{\mathrm{3}} }\:\:. \\ $$

Answered by ajfour last updated on 19/Jun/17

Commented by Tinkutara last updated on 22/Jun/17

Then this procedure is wrong? Or how to proceed further using this method?

$$\mathrm{Then}\:\mathrm{this}\:\mathrm{procedure}\:\mathrm{is}\:\mathrm{wrong}?\:\mathrm{Or}\:\mathrm{how} \\ $$$$\mathrm{to}\:\mathrm{proceed}\:\mathrm{further}\:\mathrm{using}\:\mathrm{this}\:\mathrm{method}? \\ $$

Commented by ajfour last updated on 22/Jun/17

lengths of tangent from B to excircle of radius r_1 are BD=BE =ma lengths of tangent from C to excircle of radius r_1 are CD=CF =na ma+na = a ⇒ m+n = 1 ......(i) If Δ is the area of △ABC, Area of entire figure (consider AG joined (D may or may not lie on it) is A=Δ+2[(r_1 /2)(ma)+(r_1 /2)(na)] =Δ+r_1 (ma+na) A =Δ+r_1 a (as ma+na=a) ....(ii) but A is also given by A=(1/2)(r_1 )(c+ma)+(1/2)(r_1 )(b+na) = (r_1 /2)(b+c+ma+na) A = (r_1 /2)(a+b+c) (as m+n=1) ....(iii) equating (ii) and (iii): A = (r_1 /2)(a+b+c) = Δ+r_1 a or r_1 s−r_1 a =Δ r_1 = (𝚫/(s−a)) where s=((a+b+c)/2) . similarly r_2 =(Δ/(s−b))and r_3 =(Δ/(s−c)) i am thinking how to prove..

$${lengths}\:\:{of}\:{tangent}\:{from}\:{B}\:{to} \\ $$$${excircle}\:{of}\:{radius}\:{r}_{\mathrm{1}} \:{are} \\ $$$$\:\:\:{BD}={BE}\:={ma}\: \\ $$$${lengths}\:\:{of}\:{tangent}\:{from}\:{C}\:{to} \\ $$$${excircle}\:{of}\:{radius}\:{r}_{\mathrm{1}} \:{are} \\ $$$$\:\:\:{CD}={CF}\:={na} \\ $$$$\:\:\:{ma}+{na}\:=\:{a} \\ $$$$\Rightarrow\:\:\:\boldsymbol{{m}}+\boldsymbol{{n}}\:=\:\mathrm{1}\:\:\:......\left(\boldsymbol{{i}}\right) \\ $$$${If}\:\Delta\:{is}\:{the}\:{area}\:{of}\:\bigtriangleup{ABC}, \\ $$$${Area}\:{of}\:{entire}\:{figure}\:\left({consider}\right. \\ $$$${AG}\:{joined}\:\left({D}\:{may}\:{or}\:{may}\:{not}\right. \\ $$$$\left.\:{lie}\:{on}\:{it}\right)\:{is} \\ $$$$\:\:\:\:{A}=\Delta+\mathrm{2}\left[\frac{{r}_{\mathrm{1}} }{\mathrm{2}}\left({ma}\right)+\frac{{r}_{\mathrm{1}} }{\mathrm{2}}\left({na}\right)\right] \\ $$$$\:\:\:\:\:\:\:=\Delta+{r}_{\mathrm{1}} \left({ma}+{na}\right)\: \\ $$$$\:\:\:\:\:\:{A}\:=\Delta+{r}_{\mathrm{1}} {a}\:\:\:\:\:\:\:\:\:\:\:\:\left({as}\:{ma}+{na}={a}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....\left({ii}\right) \\ $$$${but}\:{A}\:{is}\:{also}\:{given}\:{by} \\ $$$$\:{A}=\frac{\mathrm{1}}{\mathrm{2}}\left({r}_{\mathrm{1}} \right)\left({c}+{ma}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left({r}_{\mathrm{1}} \right)\left({b}+{na}\right) \\ $$$$\:\:\:\:=\:\frac{{r}_{\mathrm{1}} }{\mathrm{2}}\left({b}+{c}+{ma}+{na}\right) \\ $$$$\:\:{A}\:=\:\frac{{r}_{\mathrm{1}} }{\mathrm{2}}\left({a}+{b}+{c}\right)\:\:\:\:\:\:\:\:\:\:\:\left({as}\:{m}+{n}=\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....\left({iii}\right) \\ $$$$\:\:{equating}\:\:\:\left({ii}\right)\:{and}\:\left({iii}\right): \\ $$$$\:\:{A}\:=\:\frac{{r}_{\mathrm{1}} }{\mathrm{2}}\left({a}+{b}+{c}\right)\:=\:\Delta+{r}_{\mathrm{1}} {a} \\ $$$${or}\:\:\:\:\:\:{r}_{\mathrm{1}} {s}−{r}_{\mathrm{1}} {a}\:=\Delta \\ $$$$\:\:\:\:\:\boldsymbol{{r}}_{\mathrm{1}} \:=\:\frac{\boldsymbol{\Delta}}{{s}−{a}}\:\:\:\:\:\:\:{where}\:{s}=\frac{{a}+{b}+{c}}{\mathrm{2}}\:. \\ $$$$\:{similarly}\:\:\boldsymbol{{r}}_{\mathrm{2}} \:=\frac{\Delta}{{s}−{b}}{and}\:\boldsymbol{{r}}_{\mathrm{3}} =\frac{\Delta}{{s}−{c}} \\ $$$$\:\:{i}\:{am}\:{thinking}\:{how}\:{to}\:{prove}.. \\ $$$$ \\ $$

Commented by mrW1 last updated on 19/Jun/17

Excellent sir!

$$\mathrm{Excellent}\:\mathrm{sir}! \\ $$

Commented by ajfour last updated on 22/Jun/17

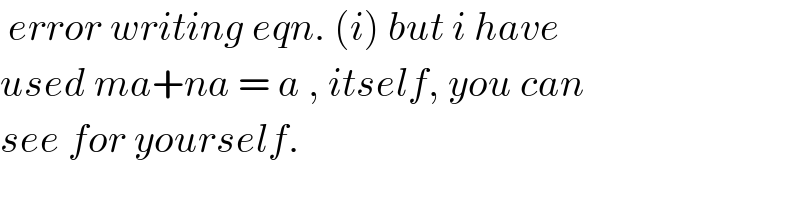
error writing eqn. (i) but i have used ma+na = a , itself, you can see for yourself.

$$\:{error}\:{writing}\:{eqn}.\:\left({i}\right)\:{but}\:{i}\:{have} \\ $$$${used}\:{ma}+{na}\:=\:{a}\:,\:{itself},\:{you}\:{can} \\ $$$${see}\:{for}\:{yourself}. \\ $$

Answered by mrW1 last updated on 20/Jun/17

Proof in an other way: The incircle of ΔABC has the radius r_i =(Δ/s) with Δ=area of ΔABC and s=((a+b+c)/2) When we extend B and C to B′ and C′, with B′C′ ∣∣ BC, see diagram, then the excircle r_1 becomes the incircle of the new triangle ΔAB′C′.

$$\mathrm{Proof}\:\mathrm{in}\:\mathrm{an}\:\mathrm{other}\:\mathrm{way}: \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{incircle}\:\mathrm{of}\:\Delta\mathrm{ABC}\:\mathrm{has}\:\mathrm{the}\:\mathrm{radius} \\ $$$$\mathrm{r}_{\mathrm{i}} =\frac{\Delta}{\mathrm{s}} \\ $$$$\mathrm{with}\:\Delta=\mathrm{area}\:\mathrm{of}\:\Delta\mathrm{ABC}\:\mathrm{and} \\ $$$$\mathrm{s}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{When}\:\mathrm{we}\:\mathrm{extend}\:\mathrm{B}\:\mathrm{and}\:\mathrm{C}\:\mathrm{to}\:\mathrm{B}'\:\mathrm{and}\:\mathrm{C}', \\ $$$$\mathrm{with}\:\mathrm{B}'\mathrm{C}'\:\mid\mid\:\mathrm{BC},\:\mathrm{see}\:\mathrm{diagram},\:\mathrm{then} \\ $$$$\mathrm{the}\:\mathrm{excircle}\:\mathrm{r}_{\mathrm{1}} \:\mathrm{becomes}\:\mathrm{the}\:\mathrm{incircle}\: \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{new}\:\mathrm{triangle}\:\Delta\mathrm{AB}'\mathrm{C}'. \\ $$

Commented by mrW1 last updated on 19/Jun/17

Commented by mrW1 last updated on 20/Jun/17

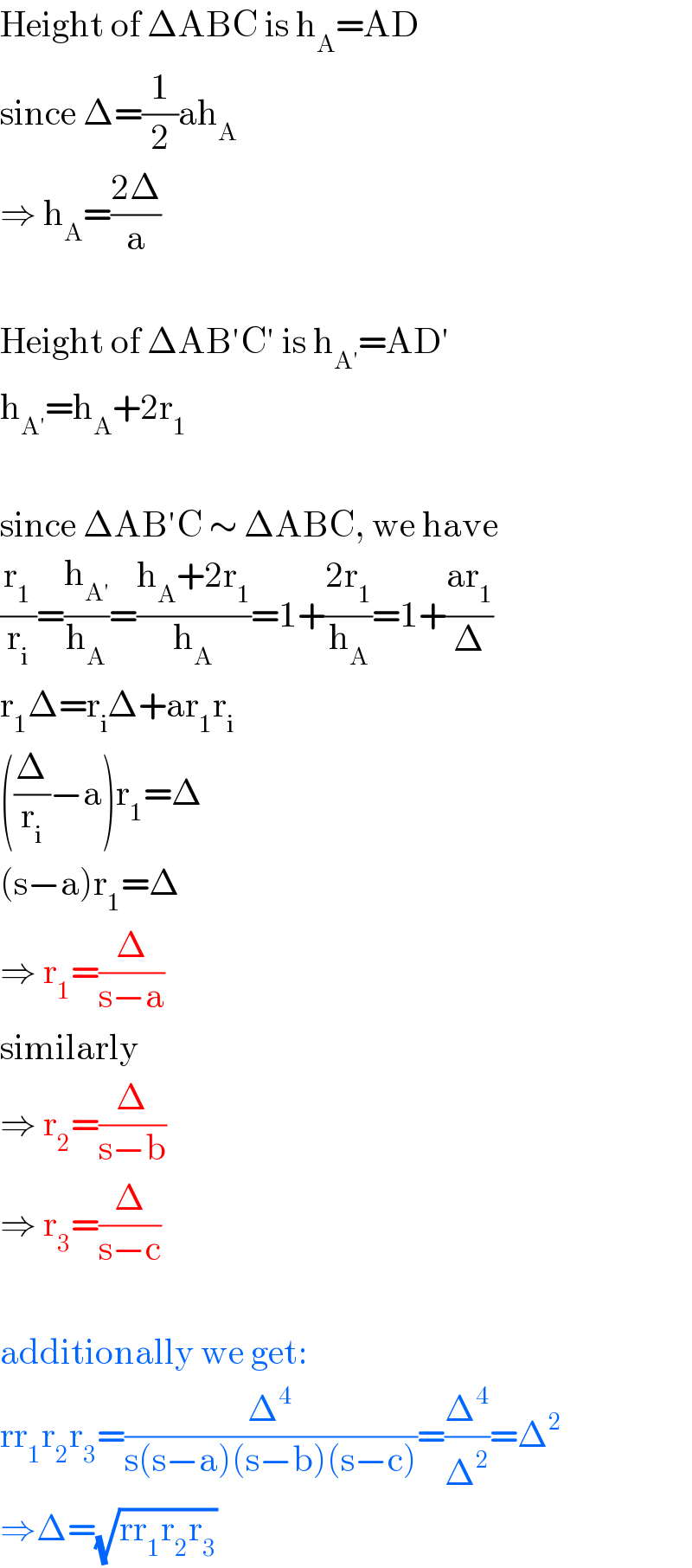
Height of ΔABC is h_A =AD since Δ=(1/2)ah_A ⇒ h_A =((2Δ)/a) Height of ΔAB′C′ is h_(A′) =AD′ h_(A′) =h_A +2r_1 since ΔAB′C ∼ ΔABC, we have (r_1 /r_i )=(h_(A′) /h_A )=((h_A +2r_1 )/h_A )=1+((2r_1 )/h_A )=1+((ar_1 )/Δ) r_1 Δ=r_i Δ+ar_1 r_i ((Δ/r_i )−a)r_1 =Δ (s−a)r_1 =Δ ⇒ r_1 =(Δ/(s−a)) similarly ⇒ r_2 =(Δ/(s−b)) ⇒ r_3 =(Δ/(s−c)) additionally we get: rr_1 r_2 r_3 =(Δ^4 /(s(s−a)(s−b)(s−c)))=(Δ^4 /Δ^2 )=Δ^2 ⇒Δ=(√(rr_1 r_2 r_3 ))

$$\mathrm{Height}\:\mathrm{of}\:\Delta\mathrm{ABC}\:\mathrm{is}\:\mathrm{h}_{\mathrm{A}} =\mathrm{AD} \\ $$$$\mathrm{since}\:\Delta=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ah}_{\mathrm{A}} \\ $$$$\Rightarrow\:\mathrm{h}_{\mathrm{A}} =\frac{\mathrm{2}\Delta}{\mathrm{a}} \\ $$$$ \\ $$$$\mathrm{Height}\:\mathrm{of}\:\Delta\mathrm{AB}'\mathrm{C}'\:\mathrm{is}\:\mathrm{h}_{\mathrm{A}'} =\mathrm{AD}' \\ $$$$\mathrm{h}_{\mathrm{A}'} =\mathrm{h}_{\mathrm{A}} +\mathrm{2r}_{\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{since}\:\Delta\mathrm{AB}'\mathrm{C}\:\sim\:\Delta\mathrm{ABC},\:\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\mathrm{r}_{\mathrm{1}} }{\mathrm{r}_{\mathrm{i}} }=\frac{\mathrm{h}_{\mathrm{A}'} }{\mathrm{h}_{\mathrm{A}} }=\frac{\mathrm{h}_{\mathrm{A}} +\mathrm{2r}_{\mathrm{1}} }{\mathrm{h}_{\mathrm{A}} }=\mathrm{1}+\frac{\mathrm{2r}_{\mathrm{1}} }{\mathrm{h}_{\mathrm{A}} }=\mathrm{1}+\frac{\mathrm{ar}_{\mathrm{1}} }{\Delta} \\ $$$$\mathrm{r}_{\mathrm{1}} \Delta=\mathrm{r}_{\mathrm{i}} \Delta+\mathrm{ar}_{\mathrm{1}} \mathrm{r}_{\mathrm{i}} \\ $$$$\left(\frac{\Delta}{\mathrm{r}_{\mathrm{i}} }−\mathrm{a}\right)\mathrm{r}_{\mathrm{1}} =\Delta \\ $$$$\left(\mathrm{s}−\mathrm{a}\right)\mathrm{r}_{\mathrm{1}} =\Delta \\ $$$$\Rightarrow\:\mathrm{r}_{\mathrm{1}} =\frac{\Delta}{\mathrm{s}−\mathrm{a}} \\ $$$$\mathrm{similarly} \\ $$$$\Rightarrow\:\mathrm{r}_{\mathrm{2}} =\frac{\Delta}{\mathrm{s}−\mathrm{b}} \\ $$$$\Rightarrow\:\mathrm{r}_{\mathrm{3}} =\frac{\Delta}{\mathrm{s}−\mathrm{c}} \\ $$$$ \\ $$$$\mathrm{additionally}\:\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{rr}_{\mathrm{1}} \mathrm{r}_{\mathrm{2}} \mathrm{r}_{\mathrm{3}} =\frac{\Delta^{\mathrm{4}} }{\mathrm{s}\left(\mathrm{s}−\mathrm{a}\right)\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right)}=\frac{\Delta^{\mathrm{4}} }{\Delta^{\mathrm{2}} }=\Delta^{\mathrm{2}} \\ $$$$\Rightarrow\Delta=\sqrt{\mathrm{rr}_{\mathrm{1}} \mathrm{r}_{\mathrm{2}} \mathrm{r}_{\mathrm{3}} } \\ $$

Commented by Tinkutara last updated on 20/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com