Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 162165 by cortano last updated on 27/Dec/21

If the ratio of the roots of equation ax^2 +2bx+c=0 is same as the ratio of the roots of px^2 +2qx+r=0 where a,b,c,p ,r are non zero real numbers . Then the value of ((b^2 /q^2 ))((p/a))((r/c)) is equal to

$$\mathrm{If}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{of}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{equation} \\ $$$$\:{ax}^{\mathrm{2}} +\mathrm{2}{bx}+{c}=\mathrm{0}\:\mathrm{is}\:\mathrm{same}\:\mathrm{as}\:\mathrm{the}\:\mathrm{ratio} \\ $$$$\:\mathrm{of}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:{px}^{\mathrm{2}} +\mathrm{2}{qx}+{r}=\mathrm{0}\:\mathrm{where} \\ $$$$\:{a},{b},{c},{p}\:,{r}\:\mathrm{are}\:\mathrm{non}\:\mathrm{zero}\:\mathrm{real}\:\mathrm{numbers} \\ $$$$.\:\mathrm{Then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\left(\frac{{b}^{\mathrm{2}} }{{q}^{\mathrm{2}} }\right)\left(\frac{{p}}{{a}}\right)\left(\frac{{r}}{{c}}\right)\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\: \\ $$

Commented by bobhans last updated on 27/Dec/21

{ ((ax^2 +2bx+c=0⇒(x_1 /x_2 )=λ)),((px^2 +2qx+r=0⇒(x_3 /x_4 )=λ)) :}⇒(x_1 /x_2 ) = (x_3 /x_4 ) ⇒(x_2 /x_4 )=(x_1 /x_3 ) { ((x_1 .x_2 = (c/a)⇒λx_2 ^2 = (c/a) ; x_1 +x_2 =−((2b)/a))),((x_3 .x_4 =(r/p)⇒λx_4 ^2 = (r/p) ; x_3 +x_4 =−((2q)/p))) :} { ((x_2 (1+λ)=−((2b)/a)⇒1+λ=−((2b)/(ax_2 )))),((x_4 (1+λ)=−((2q)/p) ⇒1+λ=−((2q)/(px_4 )))) :} ⇒((2b)/(ax_2 )) = ((2q)/(px_4 )) ; (x_2 /x_4 ) = ((bp)/(aq)) ⇒(x_1 /x_3 ) .(x_2 /x_4 ) = ((cp)/(ar)) ⇒(c/r)=((ax_1 x_2 )/(px_3 x_4 )) ∴ ((b^2 /q^2 ))((p/a))((r/c))= (((bp)/(aq)))((b/q))((1/(c/r))) = ((x_2 /x_4 ))(((ax_2 )/(px_4 )))(((px_3 x_4 )/(ax_1 x_2 )))= ((x_2 x_3 )/(x_1 x_4 )) = 1

$$\:\begin{cases}{\mathrm{ax}^{\mathrm{2}} +\mathrm{2bx}+\mathrm{c}=\mathrm{0}\Rightarrow\frac{\mathrm{x}_{\mathrm{1}} }{\mathrm{x}_{\mathrm{2}} }=\lambda}\\{\mathrm{px}^{\mathrm{2}} +\mathrm{2qx}+\mathrm{r}=\mathrm{0}\Rightarrow\frac{\mathrm{x}_{\mathrm{3}} }{\mathrm{x}_{\mathrm{4}} }=\lambda}\end{cases}\Rightarrow\frac{\mathrm{x}_{\mathrm{1}} }{\mathrm{x}_{\mathrm{2}} }\:=\:\frac{\mathrm{x}_{\mathrm{3}} }{\mathrm{x}_{\mathrm{4}} }\:\Rightarrow\frac{\mathrm{x}_{\mathrm{2}} }{\mathrm{x}_{\mathrm{4}} }=\frac{\mathrm{x}_{\mathrm{1}} }{\mathrm{x}_{\mathrm{3}} } \\ $$$$\:\begin{cases}{\mathrm{x}_{\mathrm{1}} .\mathrm{x}_{\mathrm{2}} =\:\frac{\mathrm{c}}{\mathrm{a}}\Rightarrow\lambda\mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} \:=\:\frac{\mathrm{c}}{\mathrm{a}}\:;\:\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} =−\frac{\mathrm{2b}}{\mathrm{a}}}\\{\mathrm{x}_{\mathrm{3}} .\mathrm{x}_{\mathrm{4}} =\frac{\mathrm{r}}{\mathrm{p}}\Rightarrow\lambda\mathrm{x}_{\mathrm{4}} ^{\mathrm{2}} =\:\frac{\mathrm{r}}{\mathrm{p}}\:;\:\mathrm{x}_{\mathrm{3}} +\mathrm{x}_{\mathrm{4}} =−\frac{\mathrm{2q}}{\mathrm{p}}}\end{cases} \\ $$$$\:\begin{cases}{\mathrm{x}_{\mathrm{2}} \left(\mathrm{1}+\lambda\right)=−\frac{\mathrm{2b}}{\mathrm{a}}\Rightarrow\mathrm{1}+\lambda=−\frac{\mathrm{2b}}{\mathrm{ax}_{\mathrm{2}} }}\\{\mathrm{x}_{\mathrm{4}} \left(\mathrm{1}+\lambda\right)=−\frac{\mathrm{2q}}{\mathrm{p}}\:\Rightarrow\mathrm{1}+\lambda=−\frac{\mathrm{2q}}{\mathrm{px}_{\mathrm{4}} }}\end{cases} \\ $$$$\:\:\Rightarrow\frac{\mathrm{2b}}{\mathrm{ax}_{\mathrm{2}} }\:=\:\frac{\mathrm{2q}}{\mathrm{px}_{\mathrm{4}} }\:;\:\frac{\mathrm{x}_{\mathrm{2}} }{\mathrm{x}_{\mathrm{4}} }\:=\:\frac{\mathrm{bp}}{\mathrm{aq}} \\ $$$$\:\Rightarrow\frac{\mathrm{x}_{\mathrm{1}} }{\mathrm{x}_{\mathrm{3}} }\:.\frac{\mathrm{x}_{\mathrm{2}} }{\mathrm{x}_{\mathrm{4}} }\:=\:\frac{\mathrm{cp}}{\mathrm{ar}}\:\Rightarrow\frac{\mathrm{c}}{\mathrm{r}}=\frac{\mathrm{ax}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} }{\mathrm{px}_{\mathrm{3}} \mathrm{x}_{\mathrm{4}} } \\ $$$$\:\therefore\:\left(\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{q}^{\mathrm{2}} }\right)\left(\frac{\mathrm{p}}{\mathrm{a}}\right)\left(\frac{\mathrm{r}}{\mathrm{c}}\right)=\:\left(\frac{\mathrm{bp}}{\mathrm{aq}}\right)\left(\frac{\mathrm{b}}{\mathrm{q}}\right)\left(\frac{\mathrm{1}}{\mathrm{c}/\mathrm{r}}\right) \\ $$$$\:\:=\:\left(\frac{\mathrm{x}_{\mathrm{2}} }{\mathrm{x}_{\mathrm{4}} }\right)\left(\frac{\mathrm{ax}_{\mathrm{2}} }{\mathrm{px}_{\mathrm{4}} }\right)\left(\frac{\mathrm{px}_{\mathrm{3}} \mathrm{x}_{\mathrm{4}} }{\mathrm{ax}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} }\right)=\:\frac{\mathrm{x}_{\mathrm{2}} \mathrm{x}_{\mathrm{3}} }{\mathrm{x}_{\mathrm{1}} \mathrm{x}_{\mathrm{4}} }\:=\:\mathrm{1} \\ $$

Answered by Rasheed.Sindhi last updated on 27/Dec/21

Let the roots of ax^2 +2bx+c=0 are α mα. the roots of px^2 +2qx+r=0 are β , mβ •α+mα=−((2b)/a) , mα^2 =(c/a) α=−((2b)/((1+m)a)), m(−((2b)/((1+m)a)))^2 =(c/a) •β+mβ=−((2q)/p) , mβ^2 =(r/p) β=−((2q)/((1+m)p)),m(−((2q)/((1+m)p)))^2 =(r/p) (( m(−((2b)/((1+m)a)))^2 )/(m(−((2q)/((1+m)p)))^2 ))=((c/a)/(r/p)) (( ((4b^2 )/((1+m)^2 a^2 )))/((4q^2 )/((1+m)^2 p^2 )))=((cp)/(ar)) ((4b^2 )/a^2 )×(p^2 /(4q^2 ))=((cp)/(ar)) ((b^2 p)/(aq^2 ))=(c/r)⇒((b^2 /q^2 ))((p/a))((r/c))=(c/r)((r/c))=1 ((b^2 /q^2 ))((p/a))((r/c))=1

$${Let}\:{the}\:{roots}\:{of}\:\:{ax}^{\mathrm{2}} +\mathrm{2}{bx}+{c}=\mathrm{0} \\ $$$${are}\:\alpha\:\:{m}\alpha. \\ $$$${the}\:{roots}\:{of}\:{px}^{\mathrm{2}} +\mathrm{2}{qx}+{r}=\mathrm{0}\:{are} \\ $$$$\:\beta\:,\:{m}\beta \\ $$$$\bullet\alpha+{m}\alpha=−\frac{\mathrm{2}{b}}{{a}}\:\:,\:{m}\alpha^{\mathrm{2}} =\frac{{c}}{{a}} \\ $$$$\:\:\:\alpha=−\frac{\mathrm{2}{b}}{\left(\mathrm{1}+{m}\right){a}},\:{m}\left(−\frac{\mathrm{2}{b}}{\left(\mathrm{1}+{m}\right){a}}\right)^{\mathrm{2}} =\frac{{c}}{{a}} \\ $$$$\bullet\beta+{m}\beta=−\frac{\mathrm{2}{q}}{{p}}\:,\:{m}\beta^{\mathrm{2}} =\frac{{r}}{{p}} \\ $$$$\:\:\:\:\beta=−\frac{\mathrm{2}{q}}{\left(\mathrm{1}+{m}\right){p}},{m}\left(−\frac{\mathrm{2}{q}}{\left(\mathrm{1}+{m}\right){p}}\right)^{\mathrm{2}} =\frac{{r}}{{p}} \\ $$$$\frac{\:\cancel{{m}}\left(−\frac{\mathrm{2}{b}}{\left(\mathrm{1}+{m}\right){a}}\right)^{\mathrm{2}} }{\cancel{{m}}\left(−\frac{\mathrm{2}{q}}{\left(\mathrm{1}+{m}\right){p}}\right)^{\mathrm{2}} }=\frac{\frac{{c}}{{a}}}{\frac{{r}}{{p}}} \\ $$$$\frac{\:\frac{\mathrm{4}{b}^{\mathrm{2}} }{\left(\mathrm{1}+{m}\right)^{\mathrm{2}} {a}^{\mathrm{2}} }}{\frac{\mathrm{4}{q}^{\mathrm{2}} }{\left(\mathrm{1}+{m}\right)^{\mathrm{2}} {p}^{\mathrm{2}} }}=\frac{{cp}}{{ar}} \\ $$$$\frac{\mathrm{4}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }×\frac{{p}^{\mathrm{2}} }{\mathrm{4}{q}^{\mathrm{2}} }=\frac{{cp}}{{ar}} \\ $$$$\frac{{b}^{\mathrm{2}} {p}}{{aq}^{\mathrm{2}} }=\frac{{c}}{{r}}\Rightarrow\left(\frac{{b}^{\mathrm{2}} }{{q}^{\mathrm{2}} }\right)\left(\frac{{p}}{{a}}\right)\left(\frac{{r}}{{c}}\right)=\frac{{c}}{{r}}\left(\frac{{r}}{{c}}\right)=\mathrm{1} \\ $$$$\left(\frac{{b}^{\mathrm{2}} }{{q}^{\mathrm{2}} }\right)\left(\frac{{p}}{{a}}\right)\left(\frac{{r}}{{c}}\right)=\mathrm{1} \\ $$

Answered by Ar Brandon last updated on 27/Dec/21

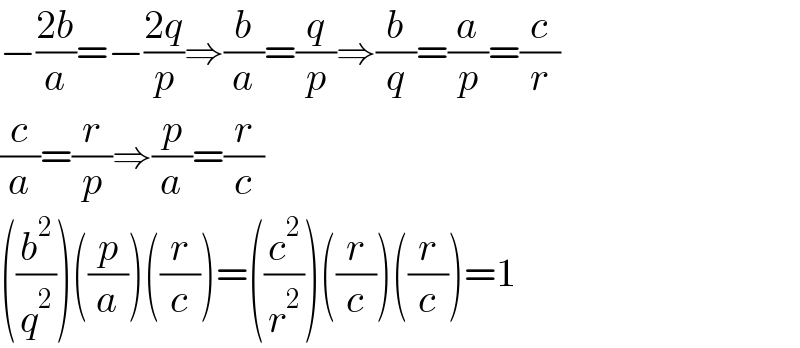
−((2b)/a)=−((2q)/p)⇒(b/a)=(q/p)⇒(b/q)=(a/p)=(c/r) (c/a)=(r/p)⇒(p/a)=(r/c) ((b^2 /q^2 ))((p/a))((r/c))=((c^2 /r^2 ))((r/c))((r/c))=1

$$−\frac{\mathrm{2}{b}}{{a}}=−\frac{\mathrm{2}{q}}{{p}}\Rightarrow\frac{{b}}{{a}}=\frac{{q}}{{p}}\Rightarrow\frac{{b}}{{q}}=\frac{{a}}{{p}}=\frac{{c}}{{r}} \\ $$$$\frac{{c}}{{a}}=\frac{{r}}{{p}}\Rightarrow\frac{{p}}{{a}}=\frac{{r}}{{c}} \\ $$$$\left(\frac{{b}^{\mathrm{2}} }{{q}^{\mathrm{2}} }\right)\left(\frac{{p}}{{a}}\right)\left(\frac{{r}}{{c}}\right)=\left(\frac{{c}^{\mathrm{2}} }{{r}^{\mathrm{2}} }\right)\left(\frac{{r}}{{c}}\right)\left(\frac{{r}}{{c}}\right)=\mathrm{1} \\ $$

Commented by Rasheed.Sindhi last updated on 27/Dec/21

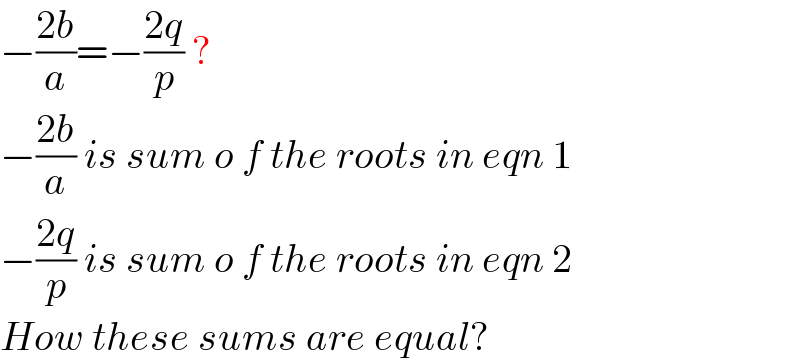
−((2b)/a)=−((2q)/p) ? −((2b)/a) is sum o f the roots in eqn 1 −((2q)/p) is sum o f the roots in eqn 2 How these sums are equal?

$$−\frac{\mathrm{2}{b}}{{a}}=−\frac{\mathrm{2}{q}}{{p}}\:? \\ $$$$−\frac{\mathrm{2}{b}}{{a}}\:{is}\:{sum}\:{o}\:{f}\:{the}\:{roots}\:{in}\:{eqn}\:\mathrm{1} \\ $$$$−\frac{\mathrm{2}{q}}{{p}}\:{is}\:{sum}\:{o}\:{f}\:{the}\:{roots}\:{in}\:{eqn}\:\mathrm{2} \\ $$$${How}\:{these}\:{sums}\:{are}\:{equal}? \\ $$

Commented by Ar Brandon last updated on 28/Dec/21

Thank you, Sir �� But I think my friend Dwaipayan Shikari was the most outstanding amongst we, the young members. I'm missing him already ���� He's been offline for a very long time even on telegram. He really motivated me a lot.

Commented by Ar Brandon last updated on 28/Dec/21

I love the way you often design your text, Sir. E.g. ThanKs Sir! 🤭

$$\mathrm{I}\:\mathrm{love}\:\mathrm{the}\:\mathrm{way}\:\mathrm{you}\:\mathrm{often}\:\mathrm{design}\:\mathrm{your}\:\mathrm{text},\:\mathrm{Sir}. \\ $$$$\mathcal{E}.{g}.\:\mathbb{T}\mathrm{han}\mathbb{K}\mathrm{s}\:\mathcal{S}{ir}! \\ $$🤭

Commented by Rasheed.Sindhi last updated on 28/Dec/21

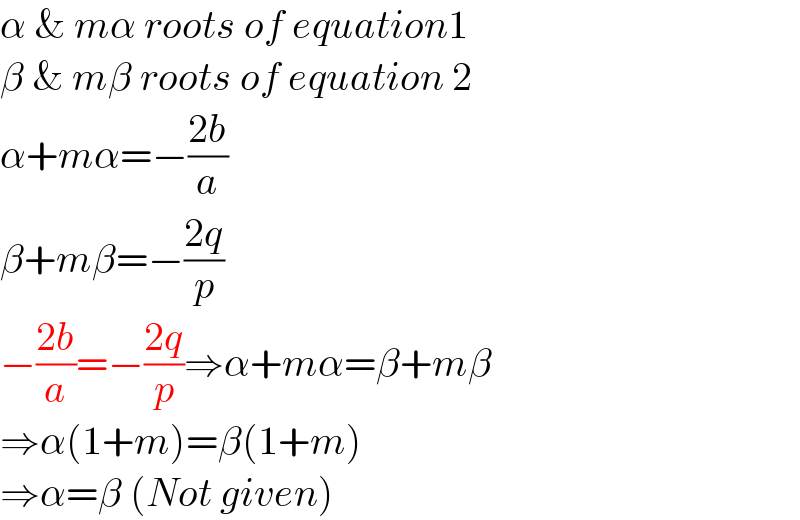
α & mα roots of equation1 β & mβ roots of equation 2 α+mα=−((2b)/a) β+mβ=−((2q)/p) −((2b)/a)=−((2q)/p)⇒α+mα=β+mβ ⇒α(1+m)=β(1+m) ⇒α=β (Not given)

$$\alpha\:\&\:{m}\alpha\:{roots}\:{of}\:{equation}\mathrm{1} \\ $$$$\beta\:\&\:{m}\beta\:{roots}\:{of}\:{equation}\:\mathrm{2} \\ $$$$\alpha+{m}\alpha=−\frac{\mathrm{2}{b}}{{a}} \\ $$$$\beta+{m}\beta=−\frac{\mathrm{2}{q}}{{p}} \\ $$$$−\frac{\mathrm{2}{b}}{{a}}=−\frac{\mathrm{2}{q}}{{p}}\Rightarrow\alpha+{m}\alpha=\beta+{m}\beta \\ $$$$\Rightarrow\alpha\left(\mathrm{1}+{m}\right)=\beta\left(\mathrm{1}+{m}\right) \\ $$$$\Rightarrow\alpha=\beta\:\left({Not}\:{given}\right) \\ $$

Commented by Ar Brandon last updated on 28/Dec/21

����

Commented by Rasheed.Sindhi last updated on 28/Dec/21

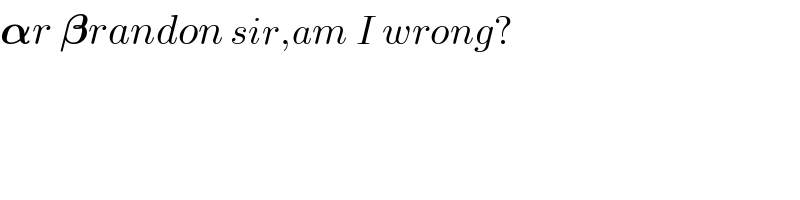
𝛂r 𝛃randon sir,am I wrong?

$$\boldsymbol{\alpha}{r}\:\boldsymbol{\beta}{randon}\:{sir},{am}\:{I}\:{wrong}? \\ $$

Commented by Ar Brandon last updated on 28/Dec/21

I'm not good enough ����

Commented by Rasheed.Sindhi last updated on 28/Dec/21

You′re more than enough good at your early stage of your life! This I say on the basis of your sent posts. (I recall that you are one of some youngest forum-friends.I′m your opposite in age as well as knowledge.) May God brightens your future!

$${You}'{re}\:{more}\:{than}\:{enough}\:{good}\:{at} \\ $$$${your}\:{early}\:{stage}\:{of}\:{your}\:{life}!\:\mathcal{T}{his} \\ $$$$\:{I}\:{say}\:{on}\:{the}\:{basis}\:{of}\:{your}\:{sent}\:{posts}. \\ $$$$\left({I}\:{recall}\:{that}\:{you}\:{are}\:{one}\:{of}\:{some}\right. \\ $$$${youngest}\:{forum}-{friends}.{I}'{m}\:{your} \\ $$$$\left.{opposite}\:{in}\:{age}\:{as}\:{well}\:{as}\:{knowledge}.\right) \\ $$$${May}\:{God}\:{brightens}\:{your}\:{future}! \\ $$

Commented by Rasheed.Sindhi last updated on 28/Dec/21

No doubt Shikari was also outstanding and I also miss him.Thank you for conversation! BTW how did you bring this emoji in a comment written by forum keyboard?

$$\mathcal{N}{o}\:{doubt}\:{Shikari}\:{was}\:{also}\:{outstanding} \\ $$$${and}\:{I}\:{also}\:{miss}\:{him}.\mathcal{T}{hank}\:{you}\:{for} \\ $$$${conversation}! \\ $$$$\mathcal{BTW}\:{how}\:{did}\:{you}\:{bring}\:{this}\:{emoji} \\ $$$${in}\:{a}\:{comment}\:{written}\:{by}\:{forum} \\ $$$${keyboard}? \\ $$

Commented by Ar Brandon last updated on 28/Dec/21

��

Commented by Ar Brandon last updated on 28/Dec/21

I clicked on line matrix then " insert plain text"

Commented by Rasheed.Sindhi last updated on 28/Dec/21

Thank you Ar Brandon! 👍👍👍😃

$$\mathcal{T}{hank}\:{you}\:{Ar}\:{Brandon}!\: \\ $$👍👍👍😃

Commented by Ar Brandon last updated on 28/Dec/21

🙃cool

🙃cool

Terms of Service

Privacy Policy

Contact: info@tinkutara.com