
Question and Answers Forum
Question Number 162399 by cortano last updated on 29/Dec/21
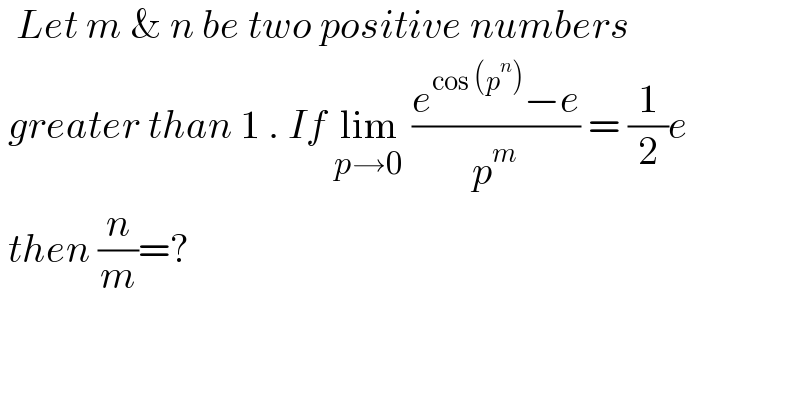
Commented byblackmamba last updated on 29/Dec/21
![lim_(p→0) ((e^(cos (p^n )) −e)/p^m ) = e lim_(p→0) ((e^(cos (p^n )−1) −1)/p^m ) = (1/2)e lim_(p→0) ((e^(cos (p^n )−1) −1)/(cos (p^n )−1)) ×lim_(p→0) ((cos (p^n )−1)/p^m ) = (1/2) [ notice that lim_(x→0) ((e^x −1)/x) = 1 ] [ lim_(p→0) ((e^(cos (p^n )−1) −1)/(cos (p^n )−1)) = 1 ] ⇔ lim_(p→0) ((cos (p^n )−1)/p^m ) = (1/2) ⇔ lim_(p→0) ((−2sin^2 ((p^n /2)))/p^m ) =(1/2) ⇔ lim_(p→0) (((((sin ((p^n /2)))/(((p^n /2)))))^2 .((p^(2n) /4)))/p^m ) =^? −(1/4) 2n=m ⇒(n/m)= (n/(2m)) = (1/2)](Q162421.png)
Answered by qaz last updated on 29/Dec/21
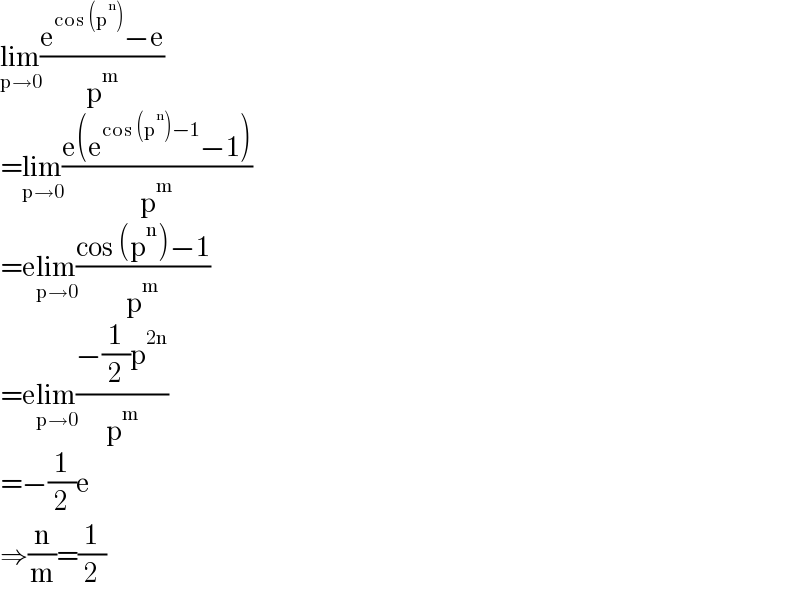
| ||
Question and Answers Forum | ||
Question Number 162399 by cortano last updated on 29/Dec/21 | ||
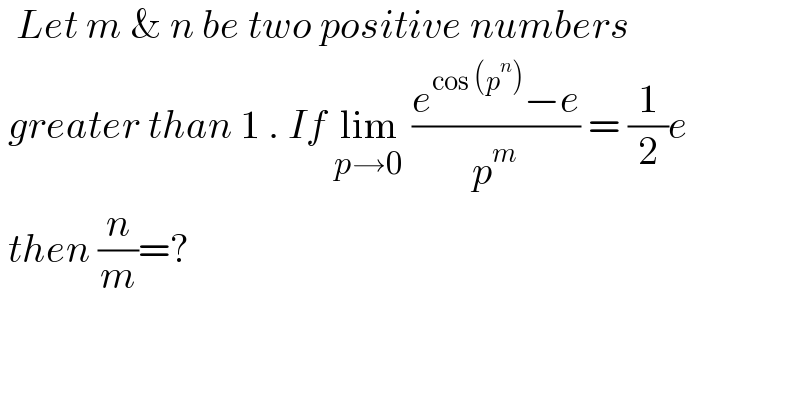 | ||
Commented byblackmamba last updated on 29/Dec/21 | ||
![lim_(p→0) ((e^(cos (p^n )) −e)/p^m ) = e lim_(p→0) ((e^(cos (p^n )−1) −1)/p^m ) = (1/2)e lim_(p→0) ((e^(cos (p^n )−1) −1)/(cos (p^n )−1)) ×lim_(p→0) ((cos (p^n )−1)/p^m ) = (1/2) [ notice that lim_(x→0) ((e^x −1)/x) = 1 ] [ lim_(p→0) ((e^(cos (p^n )−1) −1)/(cos (p^n )−1)) = 1 ] ⇔ lim_(p→0) ((cos (p^n )−1)/p^m ) = (1/2) ⇔ lim_(p→0) ((−2sin^2 ((p^n /2)))/p^m ) =(1/2) ⇔ lim_(p→0) (((((sin ((p^n /2)))/(((p^n /2)))))^2 .((p^(2n) /4)))/p^m ) =^? −(1/4) 2n=m ⇒(n/m)= (n/(2m)) = (1/2)](Q162421.png) | ||
Answered by qaz last updated on 29/Dec/21 | ||
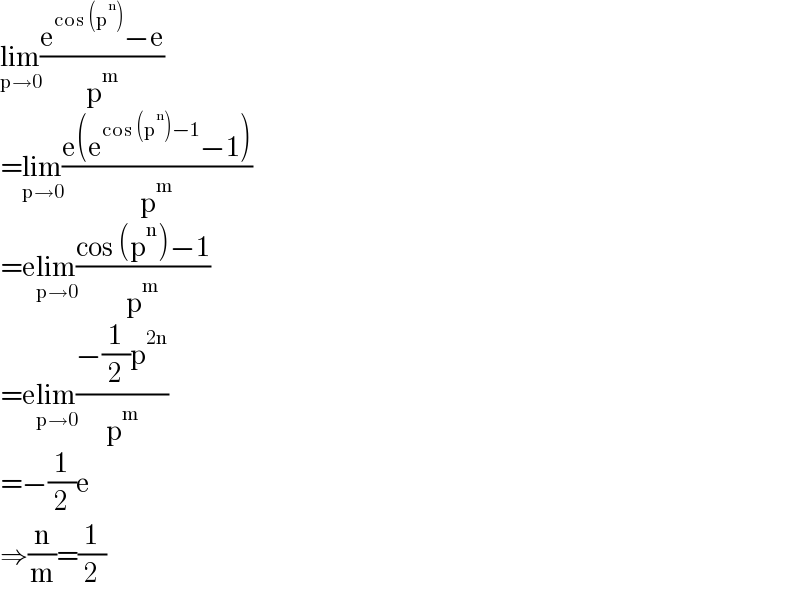 | ||
| ||