Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 162416 by HongKing last updated on 29/Dec/21

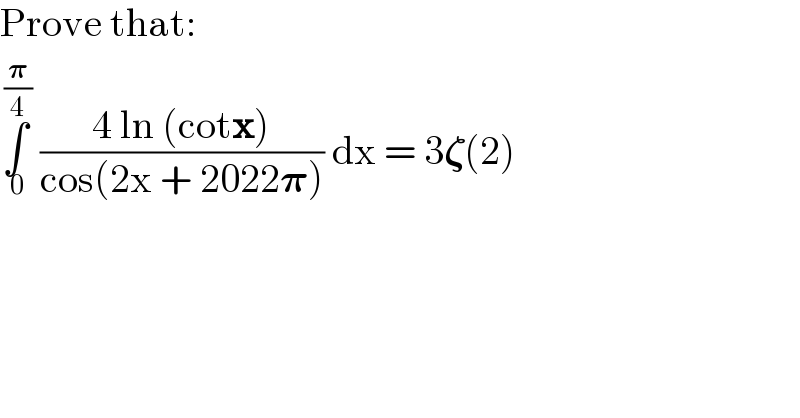
Prove that: ∫_( 0) ^( (𝛑/4)) ((4 ln (cotx))/(cos(2x + 2022𝛑))) dx = 3𝛇(2)

$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\underset{\:\mathrm{0}} {\overset{\:\frac{\boldsymbol{\pi}}{\mathrm{4}}} {\int}}\:\frac{\mathrm{4}\:\mathrm{ln}\:\left(\mathrm{cot}\boldsymbol{\mathrm{x}}\right)}{\mathrm{cos}\left(\mathrm{2x}\:+\:\mathrm{2022}\boldsymbol{\pi}\right)}\:\mathrm{dx}\:=\:\mathrm{3}\boldsymbol{\zeta}\left(\mathrm{2}\right) \\ $$

Commented by smallEinstein last updated on 29/Dec/21

Answered by mnjuly1970 last updated on 29/Dec/21

βˆ’βˆ’βˆ’ solution Ξ©= βˆ’4∫_0 ^( (Ο€/4)) (((1+tan^( 2) (x))ln( tan(x)))/(1+tan^( 2) (x)))dx =βˆ’4 ∫_0 ^( 1) (( ln (x )dx)/(1βˆ’x^( 2) )) dx = βˆ’2 ∫_0 ^( 1) (( ln(x ))/(1βˆ’x)) dx βˆ’2 ∫_0 ^( 1) ((ln(x))/(1+x))dx =βˆ’ 2 ∫_0 ^( 1) ((( ln (1βˆ’x))/x)) dx βˆ’2 Ξ¦ = 2 Li_( 2) (1 ) βˆ’ 2 Ξ¦ = 2 ΞΆ(2) βˆ’2 Ξ¦ Ξ¦ = ∫_0 ^( 1) ln(x)Ξ£_(n=0) ^∞ (βˆ’1)^( n) x^( n) = Ξ£_(n=0) ^∞ (βˆ’1)^( n) { [ (x^( n+1) /(n+1)) ln(x) ]_0 ^1 βˆ’(1/(n+1)) ∫_0 ^( 1) x^( n) dx } =Ξ£_(n=0) ^∞ (( (βˆ’1)^(n+1) )/((n+1)^( 2) )) =βˆ’ Ξ· (2) =βˆ’ ((ΞΆ (2))/2) βˆ’βˆ’βˆ’ Ξ© = 2ΞΆ (2) +ΞΆ (2) =3 ΞΆ (2) βˆ’βˆ’βˆ’β–  m.n

$$\:\:\:βˆ’βˆ’βˆ’ \\ $$$$\:\:\:\:{solution} \\ $$$$\:\:\:\Omega=\:βˆ’\mathrm{4}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \frac{\left(\mathrm{1}+{tan}^{\:\mathrm{2}} \left({x}\right)\right){ln}\left(\:{tan}\left({x}\right)\right)}{\mathrm{1}+{tan}^{\:\mathrm{2}} \left({x}\right)}{dx}\:=βˆ’\mathrm{4}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{ln}\:\left({x}\:\right){dx}}{\mathrm{1}βˆ’{x}^{\:\mathrm{2}} }\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:βˆ’\mathrm{2}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{ln}\left({x}\:\right)}{\mathrm{1}βˆ’{x}}\:{dx}\:βˆ’\mathrm{2}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=βˆ’\:\mathrm{2}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\:{ln}\:\left(\mathrm{1}βˆ’{x}\right)}{{x}}\right)\:{dx}\:βˆ’\mathrm{2}\:\Phi \\ $$$$\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\:\mathrm{Li}_{\:\mathrm{2}} \:\left(\mathrm{1}\:\right)\:βˆ’\:\mathrm{2}\:\Phi\:=\:\mathrm{2}\:\zeta\left(\mathrm{2}\right)\:βˆ’\mathrm{2}\:\Phi \\ $$$$\:\:\:\:\:\:\:\:\:\Phi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left({x}\right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(βˆ’\mathrm{1}\right)^{\:{n}} {x}^{\:{n}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(βˆ’\mathrm{1}\right)^{\:{n}} \:\left\{\:\left[\:\frac{{x}^{\:{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:{ln}\left({x}\right)\:\right]_{\mathrm{0}} ^{\mathrm{1}} βˆ’\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{\:{n}} {dx}\:\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\:\left(βˆ’\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{\:\mathrm{2}} }\:=βˆ’\:\eta\:\left(\mathrm{2}\right)\:=βˆ’\:\frac{\zeta\:\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:βˆ’βˆ’βˆ’\:\:\:\Omega\:=\:\mathrm{2}\zeta\:\left(\mathrm{2}\right)\:+\zeta\:\left(\mathrm{2}\right)\:=\mathrm{3}\:\zeta\:\left(\mathrm{2}\right)\:βˆ’βˆ’βˆ’\blacksquare\:{m}.{n}\:\:\:\:\: \\ $$$$\:\:\:\:\:\: \\ $$$$ \\ $$

Commented by HongKing last updated on 31/Dec/21

thank you so much cool my dear Sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com