
Question Number 162520 by HongKing last updated on 30/Dec/21
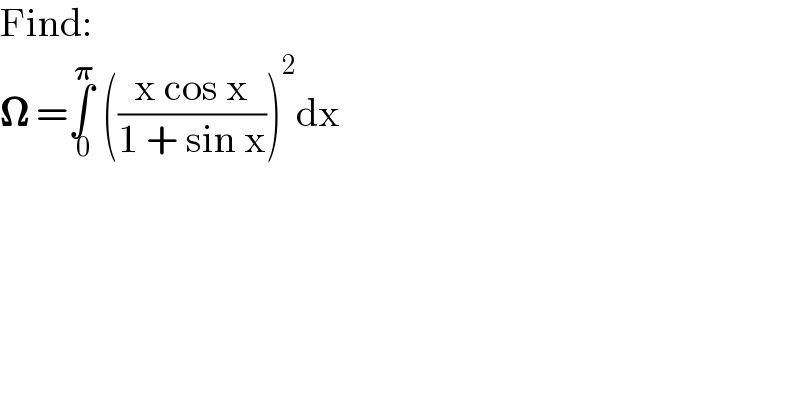
$$\mathrm{Find}: \\ $$$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\boldsymbol{\pi}} {\int}}\:\left(\frac{\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}{\mathrm{1}\:+\:\mathrm{sin}\:\mathrm{x}}\right)^{\mathrm{2}} \mathrm{dx}\: \\ $$
Answered by Ar Brandon last updated on 30/Dec/21
![Ω=∫_0 ^π (((xcosx)/(1+sinx)))^2 dx=∫_0 ^π ((x^2 cos^2 x)/((1+sinx)^2 ))dx=∫_0 ^π ((cosx)/((1+sinx)^2 ))∙(x^2 cosx)dx { ((u(x)=x^2 cosx)),((v′(x)=((cos)/((1+sinx)^2 )))) :}⇒ { ((u′(x)=−x^2 sinx+2xcosx)),((v(x)=−(1/(1+sinx)))) :} Ω=−[((x^2 cosx)/(1+sinx))]_0 ^π +∫_0 ^π ((2xcosx−x^2 sinx)/(1+sinx))dx =π^2 +2∫_0 ^π x∙((cosx)/(1+sinx))dx−∫_0 ^π ((x^2 sinx)/(1+sinx))dx =π^2 +2[xln(1+sinx)]_0 ^π −2∫_0 ^π ln(1+sinx)dx−∫_0 ^π x^2 (1−(1/(1+sinx)))dx =π^2 +0−8∫_0 ^(π/2) ln(cosu+sinu)du−(π^3 /3)+∫_0 ^π (x^2 /(1+sinx))dx =π^2 −8(G−((πln2)/4))−(π^3 /3)+∫_0 ^π (x^2 /(1+sinx))dx](Q162563.png)
$$\Omega=\int_{\mathrm{0}} ^{\pi} \left(\frac{{x}\mathrm{cos}{x}}{\mathrm{1}+\mathrm{sin}{x}}\right)^{\mathrm{2}} {dx}=\int_{\mathrm{0}} ^{\pi} \frac{{x}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} {x}}{\left(\mathrm{1}+\mathrm{sin}{x}\right)^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{cos}{x}}{\left(\mathrm{1}+\mathrm{sin}{x}\right)^{\mathrm{2}} }\centerdot\left({x}^{\mathrm{2}} \mathrm{cos}{x}\right){dx} \\ $$$$\begin{cases}{\mathrm{u}\left({x}\right)={x}^{\mathrm{2}} \mathrm{cos}{x}}\\{\mathrm{v}'\left({x}\right)=\frac{\mathrm{cos}}{\left(\mathrm{1}+\mathrm{sin}{x}\right)^{\mathrm{2}} }}\end{cases}\Rightarrow\begin{cases}{\mathrm{u}'\left({x}\right)=−{x}^{\mathrm{2}} \mathrm{sin}{x}+\mathrm{2}{x}\mathrm{cos}{x}}\\{\mathrm{v}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}{x}}}\end{cases} \\ $$$$\Omega=−\left[\frac{{x}^{\mathrm{2}} \mathrm{cos}{x}}{\mathrm{1}+\mathrm{sin}{x}}\right]_{\mathrm{0}} ^{\pi} +\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{2}{x}\mathrm{cos}{x}−{x}^{\mathrm{2}} \mathrm{sin}{x}}{\mathrm{1}+\mathrm{sin}{x}}{dx} \\ $$$$\:\:\:\:=\pi^{\mathrm{2}} +\mathrm{2}\int_{\mathrm{0}} ^{\pi} {x}\centerdot\frac{\mathrm{cos}{x}}{\mathrm{1}+\mathrm{sin}{x}}{dx}−\int_{\mathrm{0}} ^{\pi} \frac{{x}^{\mathrm{2}} \mathrm{sin}{x}}{\mathrm{1}+\mathrm{sin}{x}}{dx} \\ $$$$\:\:\:\:=\pi^{\mathrm{2}} +\mathrm{2}\left[{x}\mathrm{ln}\left(\mathrm{1}+\mathrm{sin}{x}\right)\right]_{\mathrm{0}} ^{\pi} −\mathrm{2}\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{1}+\mathrm{sin}{x}\right){dx}−\int_{\mathrm{0}} ^{\pi} {x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}{x}}\right){dx} \\ $$$$\:\:\:\:=\pi^{\mathrm{2}} +\mathrm{0}−\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cos}{u}+\mathrm{sin}{u}\right){du}−\frac{\pi^{\mathrm{3}} }{\mathrm{3}}+\int_{\mathrm{0}} ^{\pi} \frac{{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{sin}{x}}{dx} \\ $$$$\:\:\:\:=\pi^{\mathrm{2}} −\mathrm{8}\left({G}−\frac{\pi\mathrm{ln2}}{\mathrm{4}}\right)−\frac{\pi^{\mathrm{3}} }{\mathrm{3}}+\int_{\mathrm{0}} ^{\pi} \frac{{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{sin}{x}}{dx} \\ $$
Commented by HongKing last updated on 31/Dec/21
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
