
Question and Answers Forum
Question Number 162525 by mathlove last updated on 30/Dec/21
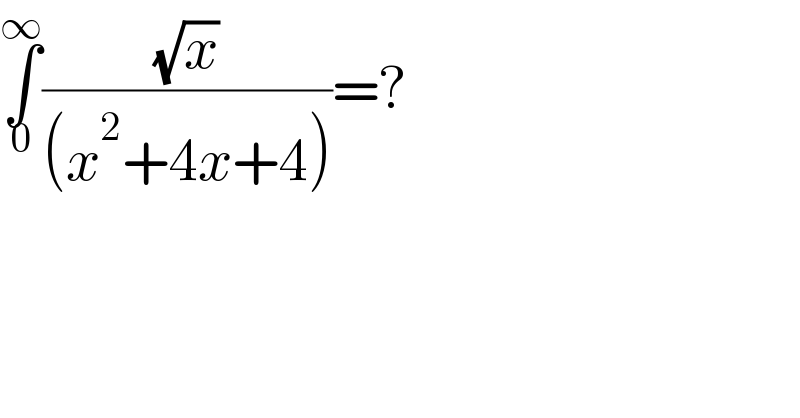
Answered by Ar Brandon last updated on 24/Mar/22
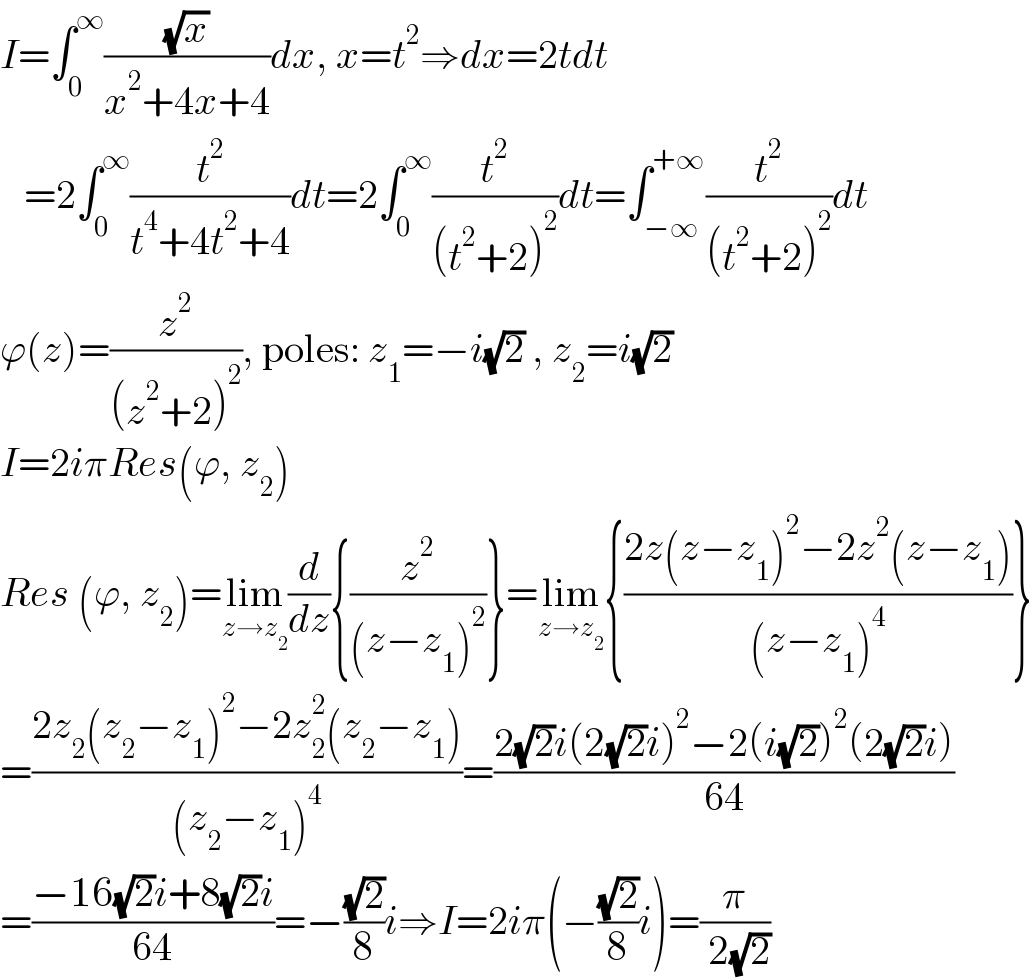
Answered by cortano last updated on 30/Dec/21
![∫_0 ^( ∞) ((√x)/(x^2 +4x+4)) dx= ∫_0 ^( ∞) ((2u^2 )/(u^4 +4u^2 +4)) du [ u=(√x) ] = ∫_0 ^( ∞) ((2u^2 )/((u^2 +2)^2 )) du = −(u/(u^2 +2 )) ∣_0 ^∞ +∫ (du/(u^2 +2)) = 0 + (1/( (√2)))[ tan^(−1) ((u/( (√2))))]_0 ^∞ = (π/(2(√2))) = ((π(√2))/4)](Q162580.png)
| ||
Question and Answers Forum | ||
Question Number 162525 by mathlove last updated on 30/Dec/21 | ||
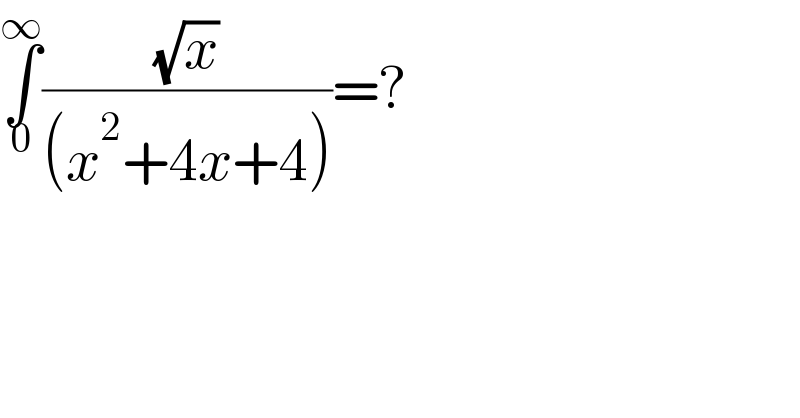 | ||
Answered by Ar Brandon last updated on 24/Mar/22 | ||
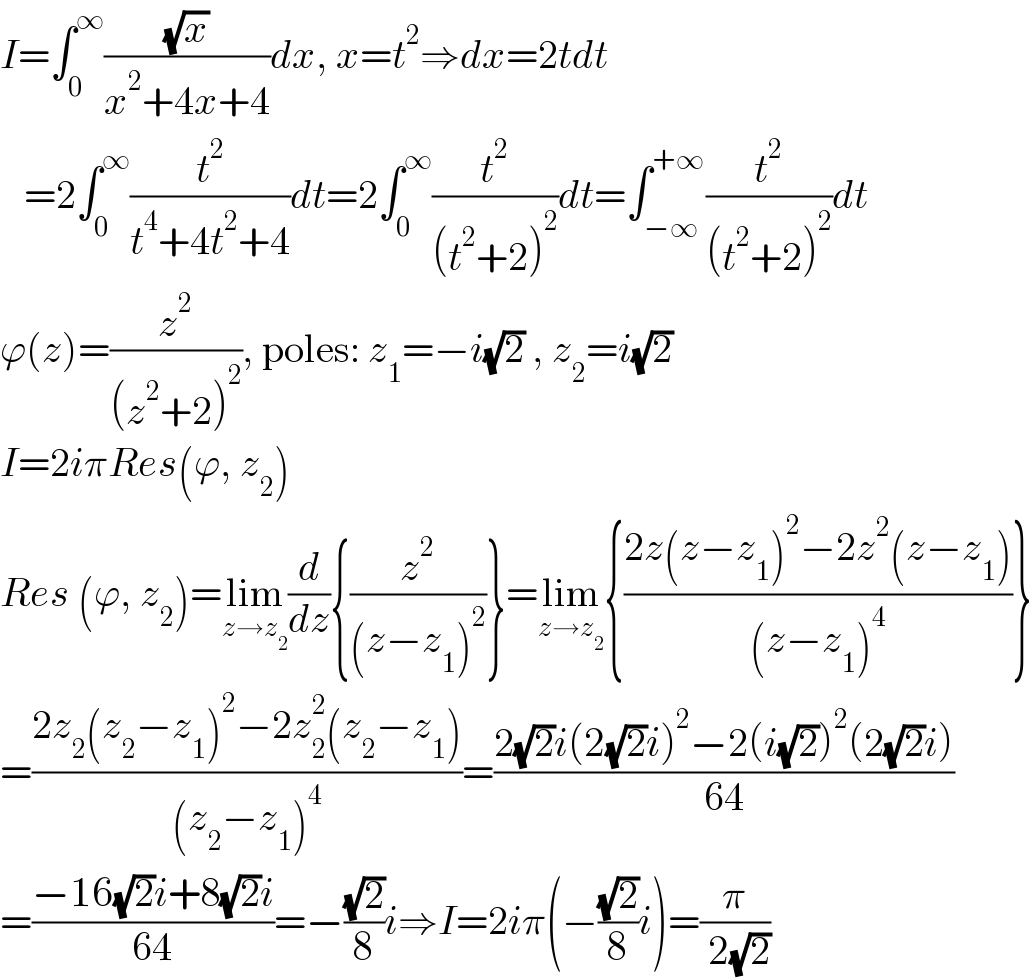 | ||
| ||
Answered by cortano last updated on 30/Dec/21 | ||
![∫_0 ^( ∞) ((√x)/(x^2 +4x+4)) dx= ∫_0 ^( ∞) ((2u^2 )/(u^4 +4u^2 +4)) du [ u=(√x) ] = ∫_0 ^( ∞) ((2u^2 )/((u^2 +2)^2 )) du = −(u/(u^2 +2 )) ∣_0 ^∞ +∫ (du/(u^2 +2)) = 0 + (1/( (√2)))[ tan^(−1) ((u/( (√2))))]_0 ^∞ = (π/(2(√2))) = ((π(√2))/4)](Q162580.png) | ||
| ||