Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 16273 by Tinkutara last updated on 20/Jun/17

If in ΔABC r_1 = r_2 + r_3 + r, prove that triangle is right angled.

$$\mathrm{If}\:\mathrm{in}\:\Delta{ABC}\:{r}_{\mathrm{1}} \:=\:{r}_{\mathrm{2}} \:+\:{r}_{\mathrm{3}} \:+\:{r},\:\mathrm{prove} \\ $$$$\mathrm{that}\:\mathrm{triangle}\:\mathrm{is}\:\mathrm{right}\:\mathrm{angled}. \\ $$

Commented by mrW1 last updated on 20/Jun/17

what is r,r_1 ,...?

$$\mathrm{what}\:\mathrm{is}\:\mathrm{r},\mathrm{r}_{\mathrm{1}} ,...? \\ $$

Commented by Tinkutara last updated on 20/Jun/17

r is the inradius of ΔABC. r_1 , r_2 and r_3 are the exradii of ΔABC opposite to angles A, B and C respectively.

$${r}\:\mathrm{is}\:\mathrm{the}\:\mathrm{inradius}\:\mathrm{of}\:\Delta{ABC}. \\ $$$${r}_{\mathrm{1}} ,\:{r}_{\mathrm{2}} \:\mathrm{and}\:{r}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{the}\:\mathrm{exradii}\:\mathrm{of}\:\Delta{ABC} \\ $$$$\mathrm{opposite}\:\mathrm{to}\:\mathrm{angles}\:{A},\:{B}\:\mathrm{and}\:{C} \\ $$$$\mathrm{respectively}. \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

p.tg(A/2)=p.tg(B/2)+p.tg(C/2)+(S/p) ⇒tg(A/2)=tg(B/2)+tg(C/2)+(S/p^2 ) tg(A/2).tg(B/2).tg(C/2)=(S/p^2 ) ⇒tg(A/2)=tg(B/2)+tg(C/2)+tg(A/2).tg(B/2).tg(C/2) ⇒tg(A/2)(1−tg(B/2).tg(C/2))=tg(B/2)+tg(C/2) ⇒tg(A/2)=((tg(B/2)+tg(C/2))/(1−tg(B/2).tg(C/2)))=tg((B/2)+(C/2))⇒ (A/2)=((B+C)/2)⇒A=B+C=180−A⇒A=90^• .■

$${p}.{tg}\frac{{A}}{\mathrm{2}}={p}.{tg}\frac{{B}}{\mathrm{2}}+{p}.{tg}\frac{{C}}{\mathrm{2}}+\frac{{S}}{{p}} \\ $$$$\Rightarrow{tg}\frac{{A}}{\mathrm{2}}={tg}\frac{{B}}{\mathrm{2}}+{tg}\frac{{C}}{\mathrm{2}}+\frac{{S}}{{p}^{\mathrm{2}} } \\ $$$${tg}\frac{{A}}{\mathrm{2}}.{tg}\frac{{B}}{\mathrm{2}}.{tg}\frac{{C}}{\mathrm{2}}=\frac{{S}}{{p}^{\mathrm{2}} } \\ $$$$\Rightarrow{tg}\frac{{A}}{\mathrm{2}}={tg}\frac{{B}}{\mathrm{2}}+{tg}\frac{{C}}{\mathrm{2}}+{tg}\frac{{A}}{\mathrm{2}}.{tg}\frac{{B}}{\mathrm{2}}.{tg}\frac{{C}}{\mathrm{2}} \\ $$$$\Rightarrow{tg}\frac{{A}}{\mathrm{2}}\left(\mathrm{1}−{tg}\frac{{B}}{\mathrm{2}}.{tg}\frac{{C}}{\mathrm{2}}\right)={tg}\frac{{B}}{\mathrm{2}}+{tg}\frac{{C}}{\mathrm{2}} \\ $$$$\Rightarrow{tg}\frac{{A}}{\mathrm{2}}=\frac{{tg}\frac{{B}}{\mathrm{2}}+{tg}\frac{{C}}{\mathrm{2}}}{\mathrm{1}−{tg}\frac{{B}}{\mathrm{2}}.{tg}\frac{{C}}{\mathrm{2}}}={tg}\left(\frac{{B}}{\mathrm{2}}+\frac{{C}}{\mathrm{2}}\right)\Rightarrow \\ $$$$\frac{{A}}{\mathrm{2}}=\frac{{B}+{C}}{\mathrm{2}}\Rightarrow{A}={B}+{C}=\mathrm{180}−{A}\Rightarrow{A}=\mathrm{90}^{\bullet} \:.\blacksquare \\ $$

Commented by Tinkutara last updated on 20/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Answered by ajfour last updated on 20/Jun/17

r_1 =(Δ/(s−a)) r_2 +r_3 +r=(Δ/(s−b))+(Δ/(s−c))+(Δ/s) when above r_1 =r_2 +r_3 +r (1/(s−a))=(1/(s−b))+(1/(s−c))+(1/s) (1/(s−a))−(1/s)=(1/(s−b))+(1/(s−c)) (a/(s(s−a)))=((2s−(b+c))/((s−b)(s−c))) (a/(s(s−a)))=(a/((s−b)(s−c))) or (s−b)(s−c)=s(s−a) bc−s(b+c)=−as bc=s(b+c−a) bc=(((a+b+c))/2)(b+c−a) 2bc=(b+c+a)(b+c−a) 2bc=b^2 +bc−ab+bc+c^2 −ac+ab +ac−a^2 ⇒ a^2 =b^2 +c^2 .

$${r}_{\mathrm{1}} =\frac{\Delta}{{s}−{a}}\: \\ $$$${r}_{\mathrm{2}} +{r}_{\mathrm{3}} +{r}=\frac{\Delta}{{s}−{b}}+\frac{\Delta}{{s}−{c}}+\frac{\Delta}{{s}} \\ $$$${when}\:{above}\:{r}_{\mathrm{1}} ={r}_{\mathrm{2}} +{r}_{\mathrm{3}} +{r} \\ $$$$\:\frac{\mathrm{1}}{{s}−{a}}=\frac{\mathrm{1}}{{s}−{b}}+\frac{\mathrm{1}}{{s}−{c}}+\frac{\mathrm{1}}{{s}} \\ $$$$\:\frac{\mathrm{1}}{{s}−{a}}−\frac{\mathrm{1}}{{s}}=\frac{\mathrm{1}}{{s}−{b}}+\frac{\mathrm{1}}{{s}−{c}} \\ $$$$\frac{{a}}{{s}\left({s}−{a}\right)}=\frac{\mathrm{2}{s}−\left({b}+{c}\right)}{\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$$\:\frac{{a}}{{s}\left({s}−{a}\right)}=\frac{{a}}{\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$${or}\:\:\:\:\left({s}−{b}\right)\left({s}−{c}\right)={s}\left({s}−{a}\right) \\ $$$$\:\:\:\:\:\:\:{bc}−{s}\left({b}+{c}\right)=−{as} \\ $$$$\:\:\:\:\:\:\:{bc}={s}\left({b}+{c}−{a}\right) \\ $$$$\:\:\:\:\:\:\:{bc}=\frac{\left({a}+{b}+{c}\right)}{\mathrm{2}}\left({b}+{c}−{a}\right) \\ $$$$\:\:\:\:\:\:\mathrm{2}{bc}=\left({b}+{c}+{a}\right)\left({b}+{c}−{a}\right) \\ $$$$\:\mathrm{2}{bc}={b}^{\mathrm{2}} +{bc}−{ab}+{bc}+{c}^{\mathrm{2}} −{ac}+{ab} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{ac}−{a}^{\mathrm{2}} \\ $$$$\:\:\Rightarrow\:\:\:\boldsymbol{{a}}^{\mathrm{2}} =\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} \:. \\ $$$$ \\ $$

Commented by Tinkutara last updated on 20/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Answered by mrW1 last updated on 20/Jun/17

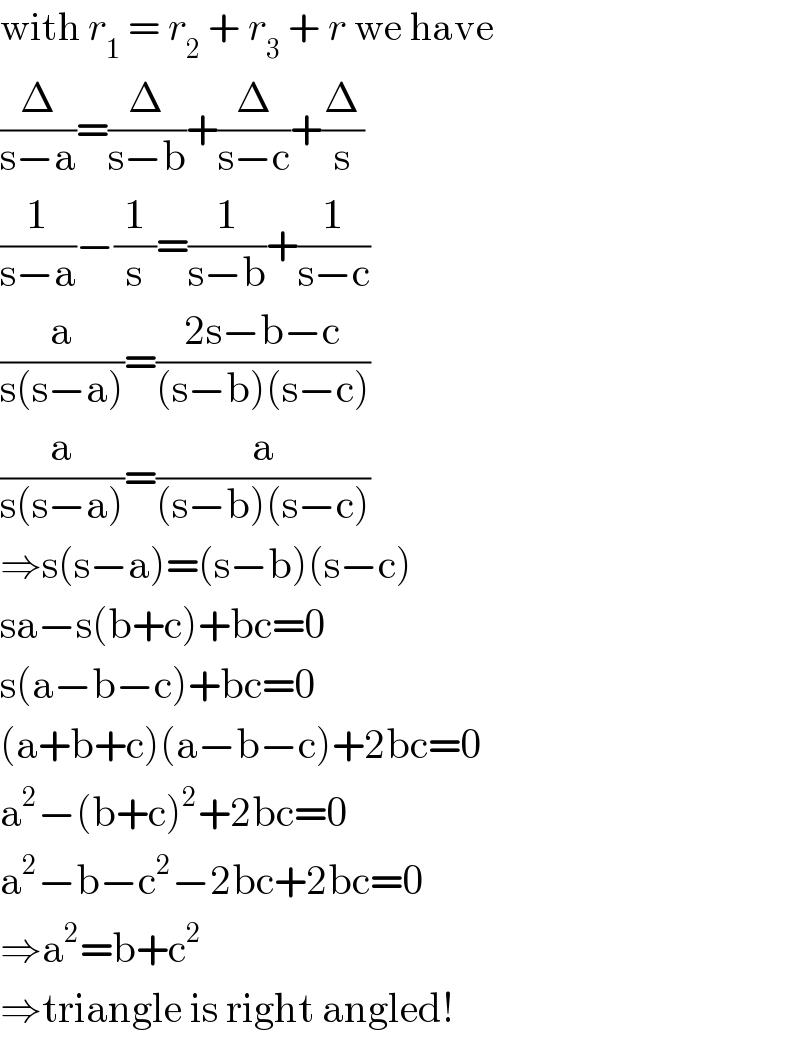
with r_1 = r_2 + r_3 + r we have (Δ/(s−a))=(Δ/(s−b))+(Δ/(s−c))+(Δ/s) (1/(s−a))−(1/s)=(1/(s−b))+(1/(s−c)) (a/(s(s−a)))=((2s−b−c)/((s−b)(s−c))) (a/(s(s−a)))=(a/((s−b)(s−c))) ⇒s(s−a)=(s−b)(s−c) sa−s(b+c)+bc=0 s(a−b−c)+bc=0 (a+b+c)(a−b−c)+2bc=0 a^2 −(b+c)^2 +2bc=0 a^2 −b−c^2 −2bc+2bc=0 ⇒a^2 =b+c^2 ⇒triangle is right angled!

$$\mathrm{with}\:{r}_{\mathrm{1}} \:=\:{r}_{\mathrm{2}} \:+\:{r}_{\mathrm{3}} \:+\:{r}\:\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\Delta}{\mathrm{s}−\mathrm{a}}=\frac{\Delta}{\mathrm{s}−\mathrm{b}}+\frac{\Delta}{\mathrm{s}−\mathrm{c}}+\frac{\Delta}{\mathrm{s}} \\ $$$$\frac{\mathrm{1}}{\mathrm{s}−\mathrm{a}}−\frac{\mathrm{1}}{\mathrm{s}}=\frac{\mathrm{1}}{\mathrm{s}−\mathrm{b}}+\frac{\mathrm{1}}{\mathrm{s}−\mathrm{c}} \\ $$$$\frac{\mathrm{a}}{\mathrm{s}\left(\mathrm{s}−\mathrm{a}\right)}=\frac{\mathrm{2s}−\mathrm{b}−\mathrm{c}}{\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right)} \\ $$$$\frac{\mathrm{a}}{\mathrm{s}\left(\mathrm{s}−\mathrm{a}\right)}=\frac{\mathrm{a}}{\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right)} \\ $$$$\Rightarrow\mathrm{s}\left(\mathrm{s}−\mathrm{a}\right)=\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right) \\ $$$$\mathrm{sa}−\mathrm{s}\left(\mathrm{b}+\mathrm{c}\right)+\mathrm{bc}=\mathrm{0} \\ $$$$\mathrm{s}\left(\mathrm{a}−\mathrm{b}−\mathrm{c}\right)+\mathrm{bc}=\mathrm{0} \\ $$$$\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}−\mathrm{b}−\mathrm{c}\right)+\mathrm{2bc}=\mathrm{0} \\ $$$$\mathrm{a}^{\mathrm{2}} −\left(\mathrm{b}+\mathrm{c}\right)^{\mathrm{2}} +\mathrm{2bc}=\mathrm{0} \\ $$$$\mathrm{a}^{\mathrm{2}} −\mathrm{b}−\mathrm{c}^{\mathrm{2}} −\mathrm{2bc}+\mathrm{2bc}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} =\mathrm{b}+\mathrm{c}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{triangle}\:\mathrm{is}\:\mathrm{right}\:\mathrm{angled}! \\ $$

Commented by Tinkutara last updated on 20/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com