Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 16277 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

in triangle:AB^Δ C,consteact 3 equilateral triangle on each sides. prove that: AL=BM=CN .

$${in}\:{triangle}:{A}\overset{\Delta} {{B}C},{consteact}\:\mathrm{3}\:{equilateral} \\ $$$${triangle}\:{on}\:{each}\:{sides}. \\ $$$${prove}\:{that}:\:\:{AL}={BM}={CN}\:. \\ $$

Answered by mrW1 last updated on 20/Jun/17

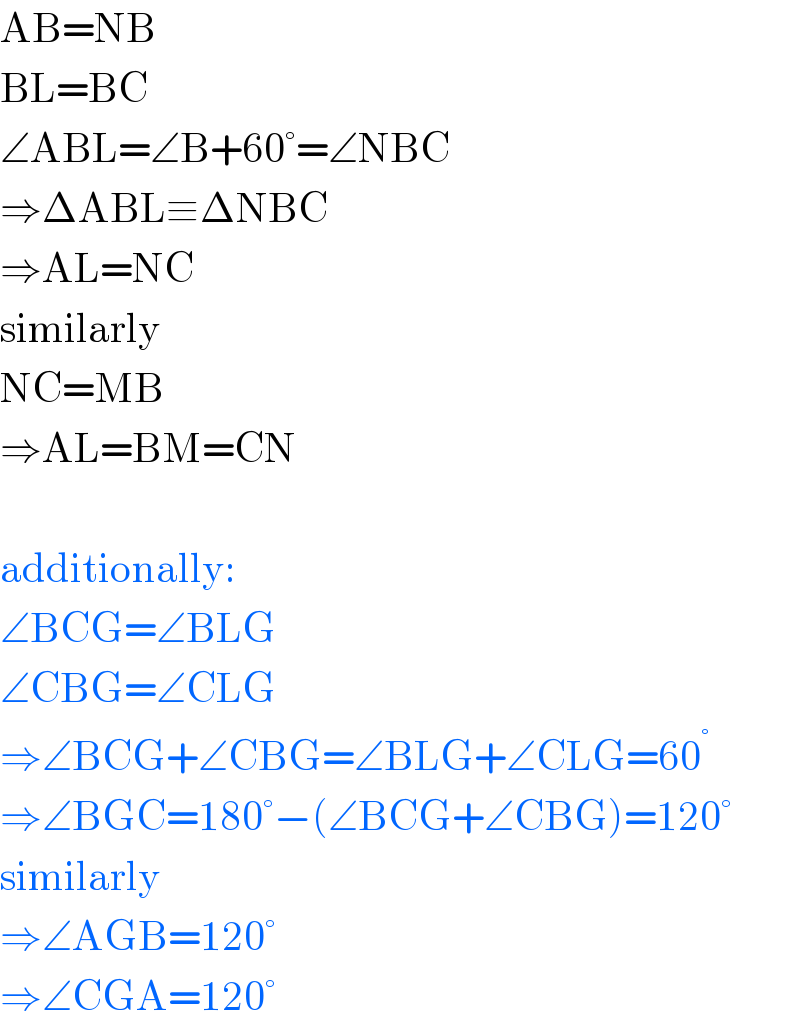
AB=NB BL=BC ∠ABL=∠B+60°=∠NBC ⇒ΔABL≡ΔNBC ⇒AL=NC similarly NC=MB ⇒AL=BM=CN additionally: ∠BCG=∠BLG ∠CBG=∠CLG ⇒∠BCG+∠CBG=∠BLG+∠CLG=60^° ⇒∠BGC=180°−(∠BCG+∠CBG)=120° similarly ⇒∠AGB=120° ⇒∠CGA=120°

$$\mathrm{AB}=\mathrm{NB} \\ $$$$\mathrm{BL}=\mathrm{BC} \\ $$$$\angle\mathrm{ABL}=\angle\mathrm{B}+\mathrm{60}°=\angle\mathrm{NBC} \\ $$$$\Rightarrow\Delta\mathrm{ABL}\equiv\Delta\mathrm{NBC} \\ $$$$\Rightarrow\mathrm{AL}=\mathrm{NC} \\ $$$$\mathrm{similarly} \\ $$$$\mathrm{NC}=\mathrm{MB} \\ $$$$\Rightarrow\mathrm{AL}=\mathrm{BM}=\mathrm{CN} \\ $$$$ \\ $$$$\mathrm{additionally}: \\ $$$$\angle\mathrm{BCG}=\angle\mathrm{BLG} \\ $$$$\angle\mathrm{CBG}=\angle\mathrm{CLG} \\ $$$$\Rightarrow\angle\mathrm{BCG}+\angle\mathrm{CBG}=\angle\mathrm{BLG}+\angle\mathrm{CLG}=\mathrm{60}^{°} \\ $$$$\Rightarrow\angle\mathrm{BGC}=\mathrm{180}°−\left(\angle\mathrm{BCG}+\angle\mathrm{CBG}\right)=\mathrm{120}° \\ $$$$\mathrm{similarly} \\ $$$$\Rightarrow\angle\mathrm{AGB}=\mathrm{120}° \\ $$$$\Rightarrow\angle\mathrm{CGA}=\mathrm{120}° \\ $$

Commented by ajfour last updated on 20/Jun/17

wonderful Sir!

$$\:{wonderful}\:{Sir}!\: \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

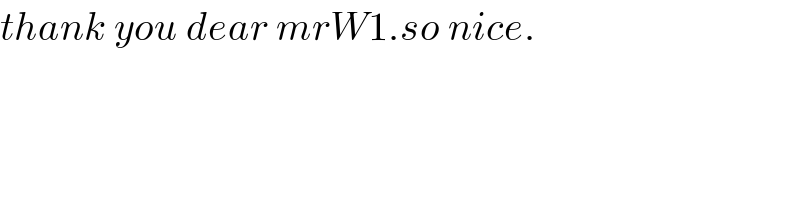
thank you dear mrW1.so nice.

$${thank}\:{you}\:{dear}\:{mrW}\mathrm{1}.{so}\:{nice}. \\ $$

Answered by ajfour last updated on 20/Jun/17

In ΔNAC CN^( 2) =b^2 +c^2 −2bccos (A+π/3) In ΔMCB BM^( 2) =a^2 +b^2 −2abcos (C+π/3) CN^( 2) −BM^( 2) = c^2 −a^2 −2b[ccos (A+π/3)−acos (C+π/3)] =c^2 −a^2 −2b{((ccos A)/2)−((c(√3)sin A)/2) −((acos C)/2)+((a(√3))/2)sin C } =c^2 −a^2 −b[ccos A−acos C] =c^2 −a^2 −b[((c(b^2 +c^2 −a^2 ))/(2bc))−((a(a^2 +b^2 −c^2 ))/(2ab))] =c^2 −a^2 −(1/2)[b^2 +c^2 −a^2 −a^2 −b^2 +c^2 ] = c^2 −a^2 −(c^2 −a^2 ) =0 Hence CN=BM similarly CN^( 2) −AL^2 =0 can be proved . ⇒ AL = BM = CN .

$$\:{In}\:\Delta{NAC}\: \\ $$$$\:{CN}^{\:\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\mathrm{cos}\:\left({A}+\pi/\mathrm{3}\right) \\ $$$$\:{In}\:\Delta{MCB} \\ $$$$\:{BM}^{\:\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\:\left({C}+\pi/\mathrm{3}\right) \\ $$$$\:{CN}^{\:\mathrm{2}} −{BM}^{\:\mathrm{2}} \:=\:{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$$−\mathrm{2}{b}\left[{c}\mathrm{cos}\:\left({A}+\pi/\mathrm{3}\right)−{a}\mathrm{cos}\:\left({C}+\pi/\mathrm{3}\right)\right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:={c}^{\mathrm{2}} −{a}^{\mathrm{2}} −\mathrm{2}{b}\left\{\frac{{c}\mathrm{cos}\:{A}}{\mathrm{2}}−\frac{{c}\sqrt{\mathrm{3}}\mathrm{sin}\:{A}}{\mathrm{2}}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{{a}\mathrm{cos}\:{C}}{\mathrm{2}}+\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:{C}\:\right\}\: \\ $$$$\:={c}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}\left[{c}\mathrm{cos}\:{A}−{a}\mathrm{cos}\:{C}\right] \\ $$$$\:={c}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}\left[\frac{{c}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}{\mathrm{2}{bc}}−\frac{{a}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)}{\mathrm{2}{ab}}\right] \\ $$$$={c}^{\mathrm{2}} −{a}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left[{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right] \\ $$$$\:=\:{c}^{\mathrm{2}} −{a}^{\mathrm{2}} −\left({c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:=\mathrm{0} \\ $$$${Hence}\:\:{CN}={BM} \\ $$$$\:{similarly}\:\:\:\:\:{CN}^{\:\mathrm{2}} −{AL}^{\mathrm{2}} \:=\mathrm{0} \\ $$$$\:{can}\:{be}\:{proved}\:. \\ $$$$\Rightarrow\:\:\:\:\:\:{AL}\:=\:{BM}\:=\:{CN}\:. \\ $$

Commented by ajfour last updated on 20/Jun/17

very foolish..

$$\:{very}\:{foolish}.. \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

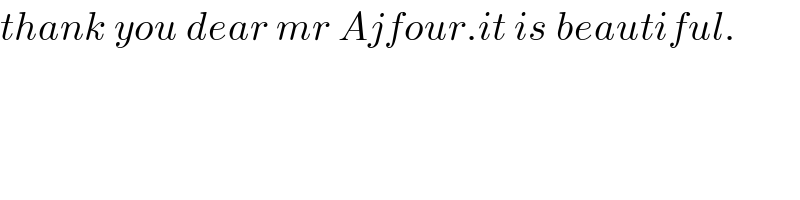
thank you dear mr Ajfour.it is beautiful.

$${thank}\:{you}\:{dear}\:{mr}\:{Ajfour}.{it}\:{is}\:{beautiful}. \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

A(a),B(b),C(c),M(m),N(n),L(l) ω^2 +ω+1=0,(1/ω)=−(1+ω),(1/ω^2 )=ω ω=((−1+i(√3))/2) c+ω.l+ω^2 .b=0⇒l=−((c+ω^2 .b)/ω)=(1+ω)(c+ω^2 .b)= =c+ω^2 .b+ω.c+ω^3 .b=b+c+ω.c+ω^2 .b b+ω.n+ω^2 .a=0⇒n=−((b+ω^2 .a)/ω)=(1+ω)(b+ω^2 .a)= =a+b+ω.b+ω^2 .a a+ω.m+ω^2 .c=0⇒m=−((a+ω^2 .c)/ω)=(1+ω)(a+ω^2 .c)= =a+c+ω.a+ω^2 .c AL=a−l=a−(b+c+ω.c+ω^2 .b)=a−b−c−ω.c+(1+ω).b= =a−b−c−ω.c+b+ω.b=(a−c)+ω(b−c)= =a−c+((−1+i(√3))/2)(b−c)=(1/2)(2a−2c−b+c+i(√3)(b−c))= AL=(1/2)(2a−b−c)+i((√3)/2)(b−c) BM=(1/2)(2b−a−c)+i((√3)/2)(c−a) CN=(1/2)(2c−a−b)+i((√3)/2)(a−b) AL^2 =(1/4)(2a−b−c)^2 +(3/4)(b−c)^2 = =(1/4)(4a^2 +b^2 +c^2 −4ab−4ac+2bc+3(b^2 +c^2 −2bc))= =(1/4)(4a^2 +4b^2 +4c^2 −4ab−4ac−4bc)= =a^2 +b^2 +c^2 −ab−ac−bc ⇒AL=BM=CN=(√(a^2 +b^2 +c^2 −ab−ac−bc)) .■

$${A}\left({a}\right),{B}\left({b}\right),{C}\left({c}\right),{M}\left({m}\right),{N}\left({n}\right),{L}\left({l}\right) \\ $$$$\omega^{\mathrm{2}} +\omega+\mathrm{1}=\mathrm{0},\frac{\mathrm{1}}{\omega}=−\left(\mathrm{1}+\omega\right),\frac{\mathrm{1}}{\omega^{\mathrm{2}} }=\omega \\ $$$$\omega=\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${c}+\omega.{l}+\omega^{\mathrm{2}} .{b}=\mathrm{0}\Rightarrow{l}=−\frac{{c}+\omega^{\mathrm{2}} .{b}}{\omega}=\left(\mathrm{1}+\omega\right)\left({c}+\omega^{\mathrm{2}} .{b}\right)= \\ $$$$={c}+\omega^{\mathrm{2}} .{b}+\omega.{c}+\omega^{\mathrm{3}} .{b}={b}+{c}+\omega.{c}+\omega^{\mathrm{2}} .{b} \\ $$$${b}+\omega.{n}+\omega^{\mathrm{2}} .{a}=\mathrm{0}\Rightarrow{n}=−\frac{{b}+\omega^{\mathrm{2}} .{a}}{\omega}=\left(\mathrm{1}+\omega\right)\left({b}+\omega^{\mathrm{2}} .{a}\right)= \\ $$$$={a}+{b}+\omega.{b}+\omega^{\mathrm{2}} .{a} \\ $$$${a}+\omega.{m}+\omega^{\mathrm{2}} .{c}=\mathrm{0}\Rightarrow{m}=−\frac{{a}+\omega^{\mathrm{2}} .{c}}{\omega}=\left(\mathrm{1}+\omega\right)\left({a}+\omega^{\mathrm{2}} .{c}\right)= \\ $$$$={a}+{c}+\omega.{a}+\omega^{\mathrm{2}} .{c} \\ $$$${AL}={a}−{l}={a}−\left({b}+{c}+\omega.{c}+\omega^{\mathrm{2}} .{b}\right)={a}−{b}−{c}−\omega.{c}+\left(\mathrm{1}+\omega\right).{b}= \\ $$$$={a}−{b}−{c}−\omega.{c}+{b}+\omega.{b}=\left({a}−{c}\right)+\omega\left({b}−{c}\right)= \\ $$$$={a}−{c}+\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\left({b}−{c}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{a}−\mathrm{2}{c}−{b}+{c}+{i}\sqrt{\mathrm{3}}\left({b}−{c}\right)\right)= \\ $$$${AL}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{a}−{b}−{c}\right)+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left({b}−{c}\right) \\ $$$${BM}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{b}−{a}−{c}\right)+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left({c}−{a}\right) \\ $$$${CN}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{c}−{a}−{b}\right)+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left({a}−{b}\right) \\ $$$${AL}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{a}−{b}−{c}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\left({b}−{c}\right)^{\mathrm{2}} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{4}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{4}{ab}−\mathrm{4}{ac}+\mathrm{2}{bc}+\mathrm{3}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{4}{b}^{\mathrm{2}} +\mathrm{4}{c}^{\mathrm{2}} −\mathrm{4}{ab}−\mathrm{4}{ac}−\mathrm{4}{bc}\right)= \\ $$$$={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{ac}−{bc} \\ $$$$\Rightarrow{AL}={BM}={CN}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{ac}−{bc}}\:.\blacksquare \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com