
Question and Answers Forum
Question Number 162775 by john_santu last updated on 01/Jan/22

Answered by mr W last updated on 01/Jan/22
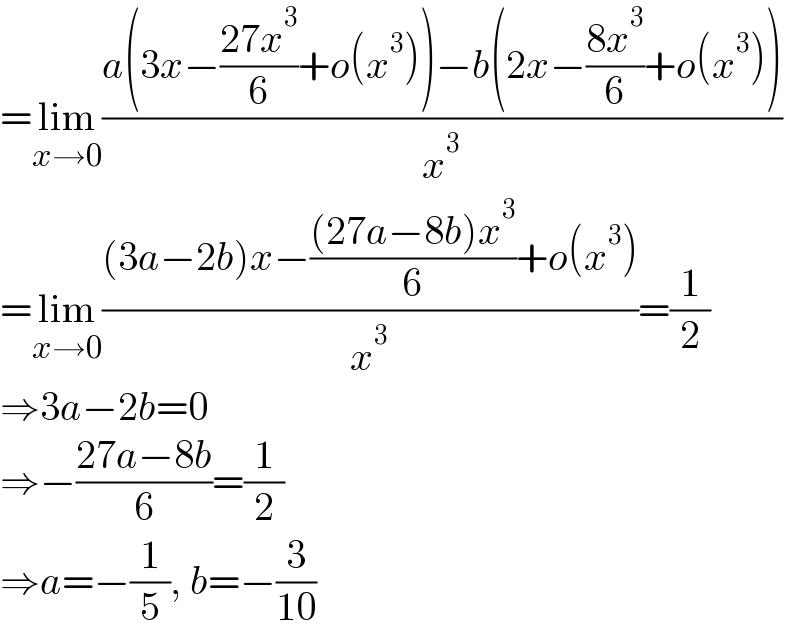
Answered by bobhans last updated on 01/Jan/22
![lim_(x→0) ((a sin 3x−3ax+3ax−2bx+2bx−b sin 2x)/x^3 ) = (1/2) lim_(x→0) ((a(sin 3x−3x)+x(3a−2b)+b(2x−sin 2x))/x^3 ) =(1/2) [ 3a=2b ] lim_(x→0) ((27a(sin 3x−3x))/((3x)^3 ))+lim_(x→0) ((8b(2x−sin 2x))/((2x)^3 )) = (1/2) −((27a)/6) +((8b)/6) = (1/2) ⇒8b−27a=3 ⇒ 4(3a)−27a = 3 → { ((−15a=3 ; a=−(1/5))),((b=−(3/(10)))) :}](Q162780.png)
| ||
Question and Answers Forum | ||
Question Number 162775 by john_santu last updated on 01/Jan/22 | ||
 | ||
Answered by mr W last updated on 01/Jan/22 | ||
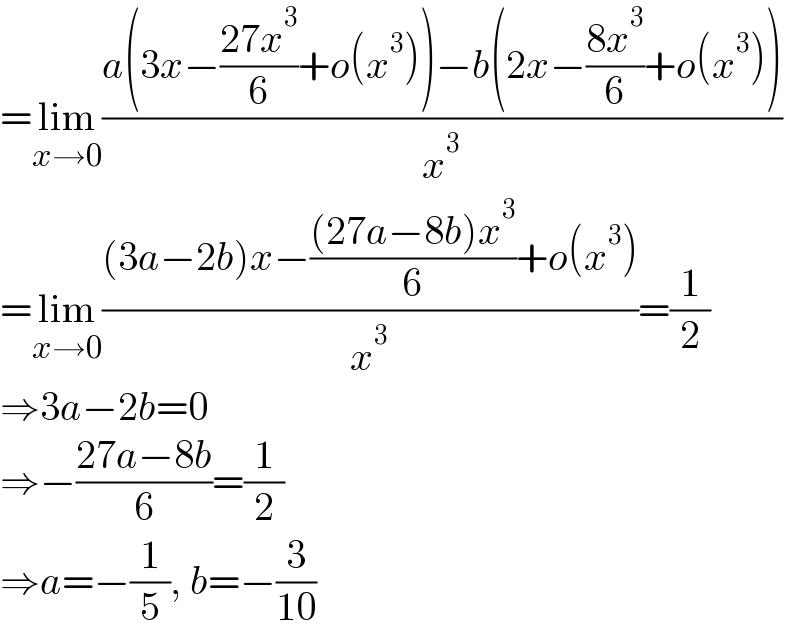 | ||
| ||
Answered by bobhans last updated on 01/Jan/22 | ||
![lim_(x→0) ((a sin 3x−3ax+3ax−2bx+2bx−b sin 2x)/x^3 ) = (1/2) lim_(x→0) ((a(sin 3x−3x)+x(3a−2b)+b(2x−sin 2x))/x^3 ) =(1/2) [ 3a=2b ] lim_(x→0) ((27a(sin 3x−3x))/((3x)^3 ))+lim_(x→0) ((8b(2x−sin 2x))/((2x)^3 )) = (1/2) −((27a)/6) +((8b)/6) = (1/2) ⇒8b−27a=3 ⇒ 4(3a)−27a = 3 → { ((−15a=3 ; a=−(1/5))),((b=−(3/(10)))) :}](Q162780.png) | ||
| ||