Question Number 162872 by amin96 last updated on 01/Jan/22
Commented by amin96 last updated on 01/Jan/22
$$\boldsymbol{{PROVE}}\:\:\:\:\:\boldsymbol{{THAT}} \\ $$
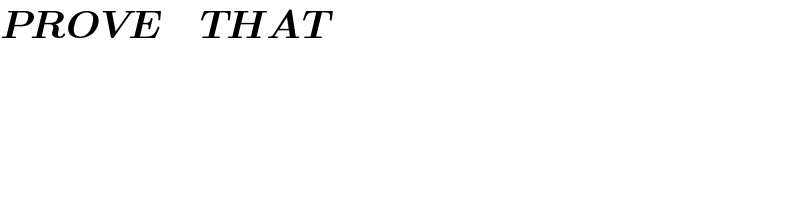
Answered by Ar Brandon last updated on 01/Jan/22
![S=Σ_(k=0) ^n e^(ikx) =((1−e^(i(n+1)x) )/(1−e^(ix) )) =((e^(i((((n+1)x)/2))) (e^(−i((((n+1)x)/2))) −e^(i((((n+1)x)/2))) ))/(e^(i(x/2)) (e^(−i(x/2)) −e^(i(x/2)) ))) =e^(i((nx)/2)) ((sin((((n+1)x)/2)))/(sin((x/2))))=((sin((((n+1)x)/2)))/(sin(x/2)))[cos((nx)/2)+isin((nx)/2)] Σ_(k=0) ^n sinkx=ImΣ_(k=0) ^n e^(ix) =((sin((((n+1)x)/2))sin(((nx)/2)))/(sin((x/2)))) =((4sin((((n+1)x)/2))sin(((nx)/2))sin((x/2)))/(4sin^2 (x/2))) =((2sin((((n+1)x)/2))[cos((((n−1)x)/2))−cos((((n+1)x)/2))])/(2(1−cosx))) =(((sin(nx)+sinx)−(sin((n+1)x))/(2−2cosx)) =((sin((n+1)x)−sin(nx)−sinx)/(2cosx−2))](Q162874.png)
$${S}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{{ikx}} =\frac{\mathrm{1}−{e}^{{i}\left({n}+\mathrm{1}\right){x}} }{\mathrm{1}−{e}^{{ix}} } \\ $$$$\:\:\:=\frac{{e}^{{i}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)} \left({e}^{−{i}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)} −{e}^{{i}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)} \right)}{{e}^{{i}\frac{{x}}{\mathrm{2}}} \left({e}^{−{i}\frac{{x}}{\mathrm{2}}} −{e}^{{i}\frac{{x}}{\mathrm{2}}} \right)} \\ $$$$\:\:\:={e}^{{i}\frac{{nx}}{\mathrm{2}}} \frac{\mathrm{sin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{{x}}{\mathrm{2}}\right)}=\frac{\mathrm{sin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)}{\mathrm{sin}\frac{{x}}{\mathrm{2}}}\left[\mathrm{cos}\frac{{nx}}{\mathrm{2}}+{i}\mathrm{sin}\frac{{nx}}{\mathrm{2}}\right] \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{sin}{kx}={Im}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{{ix}} =\frac{\mathrm{sin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{{nx}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{4sin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{{nx}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{4sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2sin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)\left[\mathrm{cos}\left(\frac{\left({n}−\mathrm{1}\right){x}}{\mathrm{2}}\right)−\mathrm{cos}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)\right]}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}{x}\right)} \\ $$$$=\frac{\left(\mathrm{sin}\left({nx}\right)+\mathrm{sin}{x}\right)−\left(\mathrm{sin}\left(\left({n}+\mathrm{1}\right){x}\right)\right.}{\mathrm{2}−\mathrm{2cos}{x}} \\ $$$$=\frac{\mathrm{sin}\left(\left({n}+\mathrm{1}\right){x}\right)−\mathrm{sin}\left({nx}\right)−\mathrm{sin}{x}}{\mathrm{2cos}{x}−\mathrm{2}} \\ $$
Commented by amin96 last updated on 02/Jan/22
$${yes}\:{sir}.\:{thank}\:{you}\:{so}\:{much} \\ $$
Commented by Ar Brandon last updated on 02/Jan/22
$$\mathrm{You}'\mathrm{re}\:\mathrm{welcome}.\:\mathrm{I}\:\mathrm{left}\:\mathrm{the}\:\mathrm{second}\:\mathrm{one}\:\mathrm{since}\:\mathrm{the}\:\mathrm{first} \\ $$$$\mathrm{one}\:\mathrm{could}\:\mathrm{serve}\:\mathrm{as}\:\mathrm{an}\:\mathrm{example}\:\mathrm{for}\:\mathrm{the}\:\mathrm{poster}. \\ $$