
Question and Answers Forum
Question Number 162949 by ajfour last updated on 02/Jan/22

Commented by ajfour last updated on 02/Jan/22

Answered by mr W last updated on 02/Jan/22

Commented by mr W last updated on 02/Jan/22
![ρ=mass of unit length m=total mass m=(πR+3R)ρ=(π+3)Rρ x=R cos φ y=((3R)/2)+R sin φ dm=ρRdφ me=∫xdm=∫_(−(π/2)) ^(π/2) R cos φ ρRdφ me=ρR^2 [sin φ]_(−(π/2)) ^(π/2) =2ρR^2 (π+3)Rρe=2ρR^2 ⇒e=((2R)/(π+3)) I_x =(((3Rρ)(3R)^2 )/3)+∫y^2 dm I_x =9ρR^3 +∫_(−(π/2)) ^(π/2) (((3R)/2)+R sin φ)^2 ρRdφ I_x =9ρR^3 +ρR^3 ∫_(−(π/2)) ^(π/2) ((3/2)+sin φ)^2 dφ I_x =9ρR^3 +ρR^3 ∫_(−(π/2)) ^(π/2) ((9/4)+3 sin φ+sin^2 φ)dφ I_x =9ρR^3 +ρR^3 ∫_(−(π/2)) ^(π/2) (((11)/4)+3 sin φ−((cos 2φ)/2))dφ I_x =9ρR^3 +ρR^3 [((11φ)/4)−3 cos φ−((sin 2φ)/4)]_(−(π/2)) ^(π/2) I_x =9ρR^3 +((11πρR^3 )/4)=(9+((11π)/4))ρR^3 ⇒I_x =(((36+11π)mR^2 )/(4(3+π))) I_y =∫x^2 dm I_y =∫_(−(π/2)) ^(π/2) R^2 cos^2 φρRdφ I_y =((ρR^3 )/2)∫_(−(π/2)) ^(π/2) (cos 2φ+1)dφ I_y =((ρR^3 )/2)[((sin 2φ)/2)+φ]_(−(π/2)) ^(π/2) I_y =((πρR^3 )/2) ⇒I_y =((πmR^2 )/(2(3+π))) I_0 =I_x +I_y =(((36+11π)mR^2 )/(4(3+π)))+((πmR^2 )/(2(3+π))) ⇒I_0 =(((36+13π)mR^2 )/(4(3+π)))](Q162976.png)
Commented by mr W last updated on 02/Jan/22

Commented by mr W last updated on 02/Jan/22
![cos ϕ=(R/(1.5R))=(2/3) ⇒ϕ=cos^(−1) (2/3) ω=(dθ/dt) α=(dω/dt)=ω(dω/dθ) I_0 α=mg(1.5R sin θ+e cos θ) (((36+13π)mR^2 )/(4(3+π)))ω(dω/dθ)=mg(((3R)/2) sin θ+((2R)/(3+π)) cos θ) ω(dω/dθ)=((2g)/((36+13π)R))[3(3+π) sin θ+4 cos θ] ∫_0 ^ω ωdω=((2g)/((36+13π)R))∫_0 ^θ [3(3+π) sin θ+4 cos θ]dθ (ω^2 /2)=((2g)/((36+13π)R))[3(3+π)(1−cos θ)+4 sin θ] ω=(√((4g)/((36+13π)R)))×(√(3(3+π)(1−cos θ)+4 sin θ)) (√(((36+13π)R)/(4g)))(dθ/( (√(3(3+π)(1−cos θ)+4 sin θ))))=dt (√(((36+13π)R)/(4g)))∫_0 ^ϕ (dθ/( (√(3(3+π)(1−cos θ)+4 sin θ))))=∫_0 ^T dt T=(√(((36+13π)R)/(4g)))∫_0 ^(cos^(−1) (2/3)) (dθ/( (√(3(3+π)(1−cos θ)+4 sin θ)))) T≈0.751917(√(((36+13π)R)/(4g)))≈3.2956(√(R/g))](Q162978.png)
Commented by ajfour last updated on 02/Jan/22
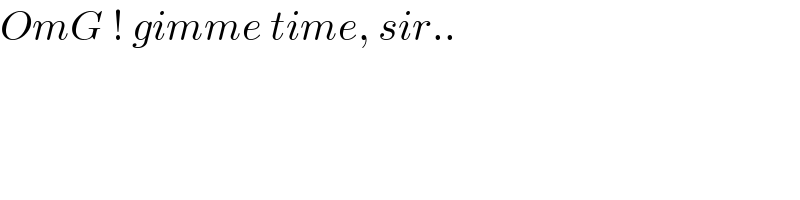
Commented by mr W last updated on 02/Jan/22
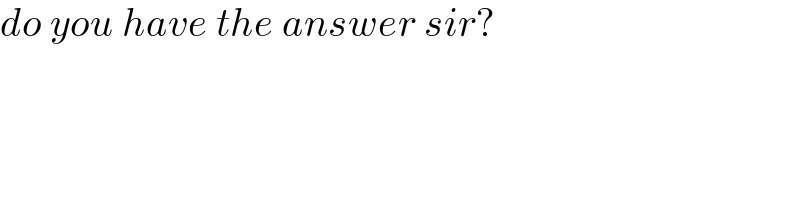
Commented by ajfour last updated on 02/Jan/22
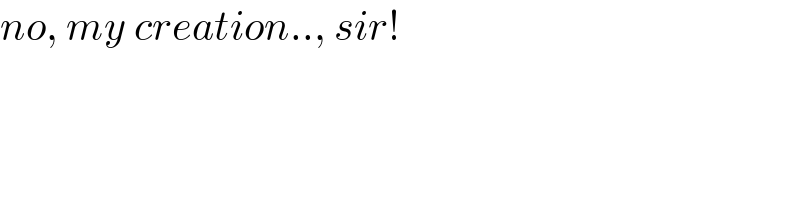
Commented by mr W last updated on 02/Jan/22
������
Commented by Ar Brandon last updated on 02/Jan/22
Is this Lekh diagram, Sir?
Commented by mr W last updated on 02/Jan/22

Commented by Tawa11 last updated on 03/Jan/22

Commented by Ar Brandon last updated on 03/Jan/22
OK
Answered by ajfour last updated on 02/Jan/22

Commented by ajfour last updated on 03/Jan/22
![Mgrcos (θ+β)+mgLcos θ=I(((ωdω)/dθ)) (ω^2 /(2g))=((Mrsin (θ+β)+mLsin θ)/I) ∫_0 ^( T) dt=(√(I/(2g)))∫_0 ^( φ) (dθ/( (√(Mrsin (θ+β)+mLsin θ)))) .... T(√((2g)/I))=∫_0 ^( φ) (dθ/( (√(M(esin θ+((3R)/2)cos θ)+m(((3R)/2)sin θ))))) cos φ=(2/3) (M/m)=((πR)/(3R))=(π/3) M((R/2))+m(0)=(M+m)e e=((R/2)/(1+(3/π)))=((πR)/(2(π+3))) I=? (i doubt, if we can easily find..) T(√((2mgR)/I))=J J=∫_0 ^( φ) (dθ/( (√([((π/6))((π/(π+3)))+(3/2)]sin θ+((π/2))cos θ)))) i can go this far, Sir!](Q162985.png)
Commented by mr W last updated on 03/Jan/22
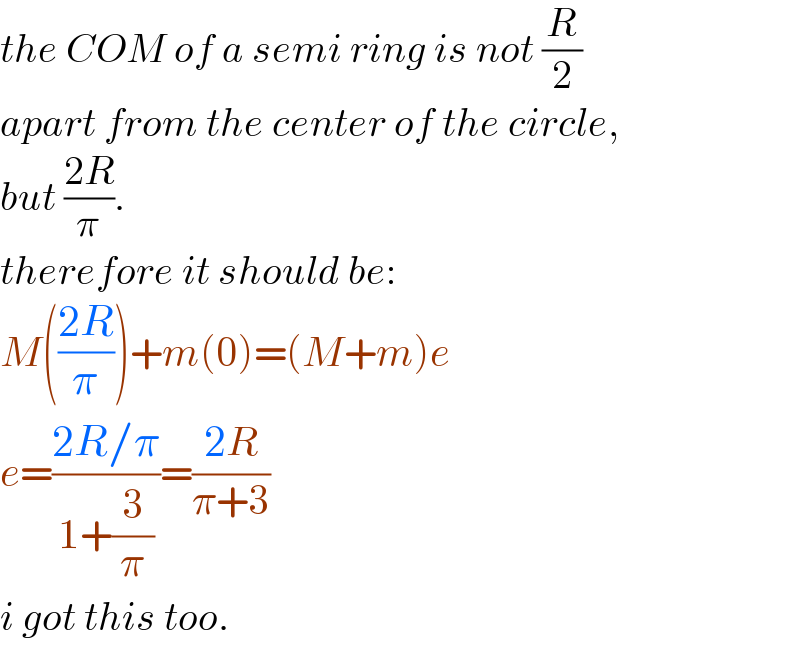
Commented by mr W last updated on 03/Jan/22

Commented by mr W last updated on 03/Jan/22
Commented by ajfour last updated on 03/Jan/22

Answered by mr W last updated on 03/Jan/22

Commented by ajfour last updated on 03/Jan/22

Commented by mr W last updated on 03/Jan/22
![cos ϕ=(2/3) e=((2R)/(3+π)) I_0 =(((36+13π)mR^2 )/(4(3+π))) r=(√(e^2 +(((3R)/2))^2 ))=(((√(97+54π+9π^2 ))R)/(2(3+π))) cos φ=((3R)/(2r))=((3(3+π))/( (√(97+54π+9π^2 )))) mgr sin θ=I_0 (ω(dω/dθ)) mgr sin θ=(((36+13π)mR^2 )/(4(3+π)))(ω(dω/dθ)) ((2g(√(97+54π+9π^2 )))/((36+13π)R)) sin θ=ω(dω/dθ) ωdω=((2g(√(97+54π+9π^2 )))/((36+13π)R)) sin θ dθ (ω^2 /2)=((2g(√(97+54π+9π^2 )))/((36+13π)R)) [cos (φ)−cos θ] ω^2 =((4g(√(97+54π+9π^2 )))/((36+13π)R)) [((3(3+π))/( (√(97+54π+9π^2 ))))−cos θ] ω^2 =(g/(a^2 R)) (b−cos θ) a=(1/2)(√((36+13π)/( (√(97+54π+9π^2 )))))≈1.009402 b=cos φ=((3(3+π))/( (√(97+54π+9π^2 ))))≈0.977236 ω=(dθ/dt)=((√(b−cos θ))/a)(√(g/R)) (√(R/g))×((adθ)/( (√(b−cos θ))))=dt T=(√(R/g)) ∫_φ ^(ϕ+φ) ((adθ)/( (√(b−cos θ))))≈3.2956(√(R/g))](Q163085.png)
Commented by mr W last updated on 03/Jan/22

