Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 163048 by mnjuly1970 last updated on 03/Jan/22

	Answered by mahdipoor last updated on 03/Jan/22
	$sin^2 x=m cos^2 x=n ⇒m^′ =−n^′ =2cosx.sinx f ′=(nm^3 +mn^3 ) ′=m′(3nm^2 +n^3 )+n′(3mn^2 +m^3 )= 2cosx.sinx(n^3 −3mn^2 +3m^2 n−m^3 )= sin2x(n−m)^3 = sin2x(cos^2 x−sin^2 x)^3 = sin2x.cos^3 2x=0 ⇒x=((kπ)/4)+(π/2) { ((sin(((kπ)/4)+(π/2))=cos(((kπ)/4)))),((cos(((kπ)/4)+(π/2))=−sin(((kπ)/2)))) :} f(((kπ)/4)+(π/2))=(1/4)sin^2 (((kπ)/2))(sin^4 (((kπ)/4))+cos^4 (((kπ)/4))) = { ((2∣k f=0)),((2∤k f=+(1/8))) :} R_f =[0,0.125]$
	${s i n}^{2} x = m {c o s}^{2} x = n$ $\Rightarrow m^{^{'}} = - n^{^{'}} = 2 c o s x . s i n x$ $f^{'} = ({n m}^{3} + {m n}^{3})^{'} = m^{'} (3 {n m}^{2} + n^{3}) + n^{'} (3 {m n}^{2} + m^{3}) =$ $2 c o s x . s i n x (n^{3} - 3 {m n}^{2} + 3 m^{2} n - m^{3}) =$ $s i n 2 x {(n - m)}^{3} =$ $s i n 2 x {({c o s}^{2} x - {s i n}^{2} x)}^{3} =$ $s i n 2 x . {c o s}^{3} 2 x = 0$ $\Rightarrow x = \frac{k π}{4} + \frac{π}{2}$ ${\begin{cases} s i n (\frac{k π}{4} + \frac{π}{2}) = c o s (\frac{k π}{4}) \\ c o s (\frac{k π}{4} + \frac{π}{2}) = - s i n (\frac{k π}{2}) \end{cases}$ $f (\frac{k π}{4} + \frac{π}{2}) = \frac{1}{4} {s i n}^{2} (\frac{k π}{2}) ({s i n}^{4} (\frac{k π}{4}) + {c o s}^{4} (\frac{k π}{4}))$ $= {\begin{cases} 2 ∣ k f = 0 \\ 2 ∤ k f = + \frac{1}{8} \end{cases}$ $R_{f} = [0, 0.125]$
	Commented by mnjuly1970 last updated on 03/Jan/22

	$m e r c e y s i r m a h d i p o o r$
	Answered by tounghoungko last updated on 03/Jan/22
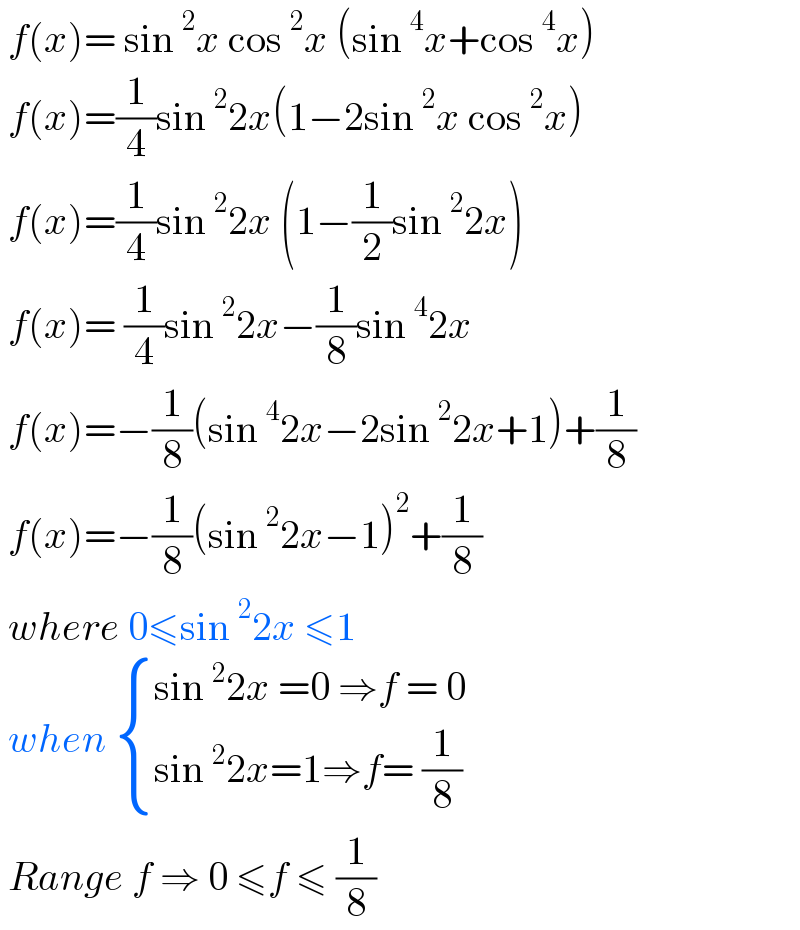
	$f(x)= sin^2 x cos^2 x (sin^4 x+cos^4 x) f(x)=(1/4)sin^2 2x(1−2sin^2 x cos^2 x) f(x)=(1/4)sin^2 2x (1−(1/2)sin^2 2x) f(x)= (1/4)sin^2 2x−(1/8)sin^4 2x f(x)=−(1/8)(sin^4 2x−2sin^2 2x+1)+(1/8) f(x)=−(1/8)(sin^2 2x−1)^2 +(1/8) where 0≤sin^2 2x ≤1 when { ((sin^2 2x =0 ⇒f = 0)),((sin^2 2x=1⇒f= (1/8))) :} Range f ⇒ 0 ≤f ≤ (1/8)$
	$f (x) = \sin^{2} x \cos^{2} x (\sin^{4} x + \cos^{4} x)$ $f (x) = \frac{1}{4} \sin^{2} 2 x (1 - 2 \sin^{2} x \cos^{2} x)$ $f (x) = \frac{1}{4} \sin^{2} 2 x (1 - \frac{1}{2} \sin^{2} 2 x)$ $f (x) = \frac{1}{4} \sin^{2} 2 x - \frac{1}{8} \sin^{4} 2 x$ $f (x) = - \frac{1}{8} (\sin^{4} 2 x - 2 \sin^{2} 2 x + 1) + \frac{1}{8}$ $f (x) = - \frac{1}{8} {(\sin^{2} 2 x - 1)}^{2} + \frac{1}{8}$ $w h e r e 0 ⩽ \sin^{2} 2 x ⩽ 1$ $w h e n {\begin{cases} \sin^{2} 2 x = 0 \Rightarrow f = 0 \\ \sin^{2} 2 x = 1 \Rightarrow f = \frac{1}{8} \end{cases}$ $R a n g e f \Rightarrow 0 ⩽ f ⩽ \frac{1}{8}$
	Commented by mnjuly1970 last updated on 03/Jan/22

	$v e r y n i c e s o l u t i o n s i r$
	Answered by abdullahhhhh last updated on 03/Jan/22

	Commented by mnjuly1970 last updated on 03/Jan/22

	$t h a n k s a l o t m a s t e r$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum