
Question and Answers Forum
Question Number 163119 by tounghoungko last updated on 04/Jan/22
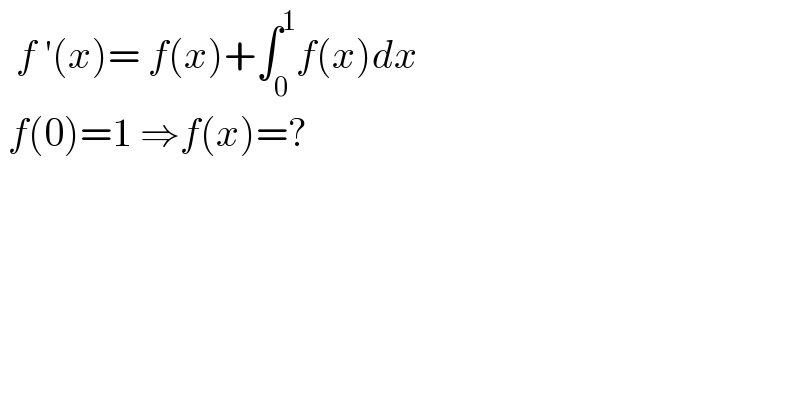
Answered by mr W last updated on 04/Jan/22
![y′=y+k with k=∫_0 ^1 f(x)dx (dy/(y+k))=dx ∫(dy/(y+k))=∫dx ln (y+k)=x+C_1 y+k=Ce^x y=f(x)=Ce^x −k ∫_0 ^1 f(x)dx=[Ce^x −kx]_0 ^1 =C(e−1)−k=^! k ⇒C=((2k)/(e−1)) f(x)=(((2e^x )/(e−1))−1)k f(0)=((2/(e−1))−1)k=^! 1 ⇒k=((e−1)/(3−e)) ⇒f(x)=(((e−1)/(3−e)))(((2e^x )/(e−1))−1)](Q163121.png)
Commented by Tawa11 last updated on 04/Jan/22

Answered by tounghoungko last updated on 04/Jan/22

| ||
Question and Answers Forum | ||
Question Number 163119 by tounghoungko last updated on 04/Jan/22 | ||
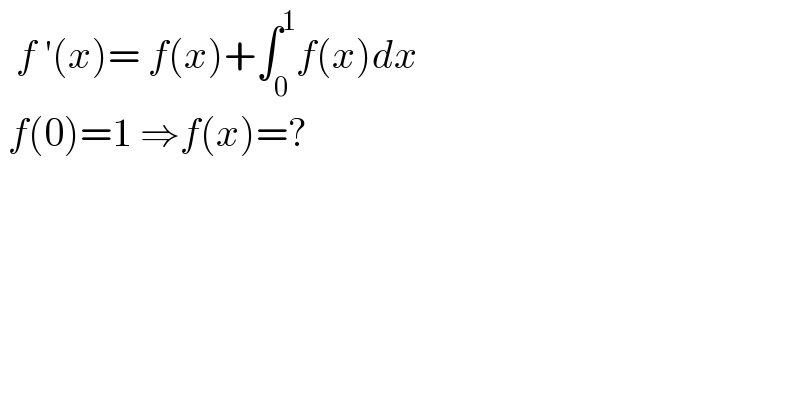 | ||
Answered by mr W last updated on 04/Jan/22 | ||
![y′=y+k with k=∫_0 ^1 f(x)dx (dy/(y+k))=dx ∫(dy/(y+k))=∫dx ln (y+k)=x+C_1 y+k=Ce^x y=f(x)=Ce^x −k ∫_0 ^1 f(x)dx=[Ce^x −kx]_0 ^1 =C(e−1)−k=^! k ⇒C=((2k)/(e−1)) f(x)=(((2e^x )/(e−1))−1)k f(0)=((2/(e−1))−1)k=^! 1 ⇒k=((e−1)/(3−e)) ⇒f(x)=(((e−1)/(3−e)))(((2e^x )/(e−1))−1)](Q163121.png) | ||
| ||
Commented by Tawa11 last updated on 04/Jan/22 | ||
 | ||
Answered by tounghoungko last updated on 04/Jan/22 | ||
 | ||